Большая часть процессов современного мира изменяются во времени. Для математического представления такого рода данных используется понятие временного ряда, которое означает последовательность упорядоченных во времени числовых показателей, характеризующих уровень состояния и изменения изучаемого явления. Такие наборы данных полезно анализировать, чтобы находить некоторые статистические закономерности и полезные характеристики ряда, что поможет в понимании природы данных и будущем моделировании. Одна из главных целей анализа и изучения временных рядов – их прогнозирование. Это часто используется в экономике, бизнесе для предсказывания будущих тенденций. Оценка возможного поведения системы позволяет принимать взвешенные решения, а также повысить эффективность выполняемой деятельности и снизить риски провала. Выбор наиболее точного алгоритма и правильная предварительная обработка данных позволяет повышать качество получаемого прогноза. Поскольку временные ряды возникают во многих предметных областях и имеют различную природу, можно сделать вывод об актуальности темы данной статьи для любых сфер бизнеса.
В общем случае временной ряд можно представить из четырех различных компонент:
- Сезонной компоненты (обозначается St, где t – момент времени), отражающей повторяемость экономических процессов в течение не очень длительного периода (года, иногда месяца, недели и т. д.).
- Тренда (Tt) – долговременной тенденции изменения исследуемого временного ряда. Тренды могут быть описаны различными уравнениями – линейными, логарифмическими, степенными и так далее.
- Циклической компоненты (Ct), отражающей повторяемость экономических процессов в течение длительных периодов.
- Случайной, нерегулярной компоненты (Et), отражающей влияние не поддающихся учету и регистрации случайных факторов.
Если временной ряд представляется в виде суммы соответствующих компонент, то полученная модель носит название аддитивной (1), если в виде произведения – мультипликативной (2) или смешанного типа (3) [1]:
Yt=Tt+St+Ct+Et, (1)
Yt=Tt+St+Ct+Et, (2)
Yt=Tt+St+Ct+Et, (3)
где: Yt – уровни временного ряда; Tt – трендовая составляющая; St – сезонная компонента; Ct – циклическая компонента; Et – случайная компонента.
Выявление структуры временного ряда необходимо для того, чтобы построить математическую модель того явления, которое выступает источником анализируемого временного ряда. Прогноз будущих значений временного ряда используется для эффективного принятия решений и широко применяется в различных сферах жизни общества.
Декомпозируем ряд, чтобы узнать, какие компоненты оказывают наибольшее влияние на его дисперсию.

Рис. 1. Пример декомпозиции временного ряда
Серые вертикальные столбцы, изображенные слева от графиков, отражают удельный вклад каждой компоненты в общую дисперсию в данных. В приведенном на рисунке 1 примере длина столбца на графике сезонной компоненты значительно больше длины столбца у исходного ряда, что указывает на незначительный вклад сезонной компоненты в общую дисперсию. В то же время длина столбца на графике остатков и тренда сравнима с длиной столбца на графике с исходными данными, что указывает на значительный вклад случайных факторов и тренда в общую дисперсию. Это говорит о нестационарности временного ряда.
Перед тем, как перейти к моделированию, стоит сказать о таком важном свойстве временного ряда как стационарность. Стационарные ряды характеризуются постоянством средних значений и дисперсий его величин. В нестационарных рядах прослеживается основная тенденция их эволюции. Поскольку большинство моделей временных рядов так или иначе моделируют и предсказывают статистические характеристики ряда, то в случае нестационарности исходного ряда предсказания окажутся неверными.
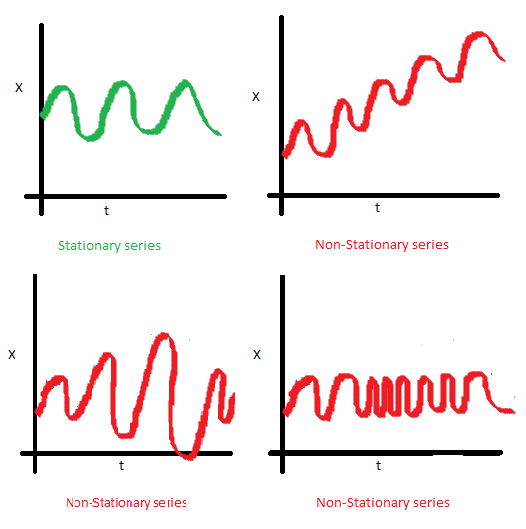
Рис. 2. Пример стационарного и нестационарных рядов
Для того чтобы привести ряд к стационарному виду можно: взять разности различного порядка, выделить тренд и сезонность или логарифмировать [2].
Чтобы проверить, стал ряд стационарным или нет, можно воспользоваться расширенным тестом Дики-Фуллера. Это один из основных методов проверки ряда на стационарность. В основе этого теста лежит предпосылка, что любой ряд можно аппроксимировать с заданной точностью процессом типа AR(p) необходимого порядка:
yt=α1yt-1+α2yt-2+…+αpyt-p+εt,
где yt – переменная, представляющая интерес, t – индекс времени, εt – ошибки, α – константа, p – порядок запаздывания авторегрессионного процесса.
Существует три спецификации расширенного теста Дики-Фуллера:
1. Без константы:
 (5)
(5)
где γ=α1-1, ∆yt – разностный оператор.
2. С константой:
 (6)
(6)
3. С трендом и константой:
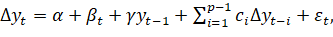 (7)
(7)
где β – коэффициент на временной тренд.
Для каждой спецификации нулевая и альтернативная гипотезы выглядят следующим образом:
H0: γ=0, процесс нестационарен
H1: γ<0, процесс стационарен
После приведения временного ряда к стационарному виду, можно приступать к его прогнозированию.
Прогнозирование временного ряда
Прогнозирование временных рядов заключается в построении модели для предсказания будущих событий основываясь на известных событиях прошлого, предсказания будущих данных до того, как они будут измерены.
Модели временных рядов – математические модели прогнозирования, которые стремятся найти зависимость будущего значения от прошлого внутри самого процесса и на этой зависимости вычислить прогноз. Эти модели универсальны для различных предметных областей, то есть их общий вид не меняется в зависимости от природы временного ряда [3].
Осуществим прогноз на тестовом периоде с использованием трёх основных методов прогнозирования:
1. Наивное прогнозирование – самый простой способ прогнозирования временных рядов. Существует несколько подходов: простой наивный и наивный с сезонностью. В первом случае все предельно просто: прогноз на завтра – это то, что мы наблюдаем сегодня. Второй случай немного более «сложен»: прогноз на завтра – это то, что мы наблюдали за неделю/месяц/год (в зависимости от того, с каким периодом мы работаем) раньше. Мы будем использовать наивное прогнозирование с сезонностью.
2. Авторегрессивнное интегрированное скользящее среднее (ARIMA) – в основу авторегрессионных моделей заложено предположение о том, что значение процесса линейно зависит от некоторого количества предыдущих значений того же процесса. ARIMA является очень важной частью статистики, эконометрики и, в частности, анализа временных рядов. Она состоит из трех элементов:
- AR (p): авторегрессионная часть модели. Означает, что мы используем p прошлых наблюдений из временного ряда в качестве предикторов.
- Разность (d): используется для преобразования временного ряда в стационарный, принимая разность между последовательными наблюдениями с соответствующими задержками d.
- MA (q): в качестве предикторов использует q ошибок прошлого прогноза.
Модели ARIMA определены для стационарных временных рядов. Следовательно, если вы начнете с нестационарного временного ряда, вам сначала нужно будет брать дифференцировать временные ряды, пока вы не достигнете стационарного временного ряда [4].
3. Экспоненциальное сглаживание – чаще всего применяется для моделирования финансовых и экономических процессов. Есть много способов осуществить экспоненциальное сглаживание. Идея состоит в том, чтобы наблюдениям всегда уделялось все меньше внимания. Прогнозы, полученные с использованием методов экспоненциального сглаживания, представляют собой средневзвешенные значения прошлых наблюдений, причем веса экспоненциально убывают по мере того, как наблюдения становятся старше. Эта структура генерирует надежные прогнозы быстро и для широкого диапазона временных рядов, что является большим преимуществом [5].
Для оценки точности нескольких моделей прогнозирования необходимо разделить исходный временной ряд на тренировочный и тестовый периоды. В науке о данных тренировочный набор – это набор данных, который используется для выявления возможных взаимосвязей. Тестовый набор – это набор данных, который используется для проверки силы этих потенциальных отношений.
Чтобы оценить, насколько эффективно работают различные методы прогнозирования на исследуемых данных, необходимо применить показатели ошибки прогноза, которые с различных сторон охарактеризуют отклонения фактических и прогнозируемых значений. Обычно для измерения точности прогнозирования модели используются три статистических показателя: средняя абсолютная ошибка, среднеквадратичная ошибка и средняя абсолютная процентная ошибка. Этих трех показателей достаточно для отражения точности прогнозирования модели.
Для прогноза исходных данных необходимо выбрать модель, значения показателей которой являются наименьшими для тестового набора данных.

Рис. 3. Пример прогноза
Таким образом, вне зависимости от используемого метода, прогнозирование требуется во многих ситуациях: прогнозы погоды, будущего спроса на товары, цен акций, потребности в запасах, объемов экспорта и импорта и многое другое. Прогнозы могут потребоваться на несколько лет вперед (в случае капитальных вложений) или всего за несколько минут (для маршрутизации телекоммуникаций). Какими бы ни были обстоятельства или временные рамки, прогнозирование является важным подспорьем для эффективного и действенного планирования.

.png&w=640&q=75)