Анализ устойчивости системы точения позволяет выявлять условия перехода технологической системы из устойчивого в неустойчивое состояние. Знание условий потери устойчивости в будущем позволить сформировать принципы, позволяющие повысить надежность функционирования технологической системы.
Рассмотрим математическую модель нелинейной динамики процесса точения. Для её построения были приняты следующие базовые гипотезы и допущения:
- рассматривается только подсистема режущего инструмента;
- режущий инструмент может совершать упругие деформационные смещения только в радиальном направлении Y(t);
- процесс резания потенциально является возмущенным;
- сила резания (радиальная составляющая силы резания) определяется на основании уравнения И.А. Тиме;
- учитывается сила контактного взаимодействия Fs(∆) между задней поверхностью режущего клина резца и обработанной поверхности заготовки, которая является нелинейной характеристикой процесса точения.
На основании выше введенных гипотез и допущений получим следующую концептуальную схему технологической системы, которая представлена на рисунке 1.
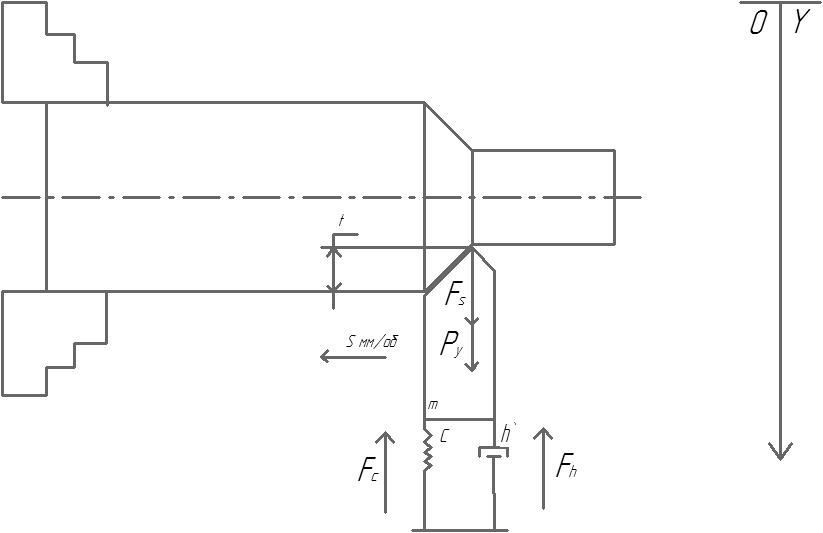
Рис. 1. Концептуальная модель динамики технологической системы
Тогда математическая модель динамики процесса точения в вариациях относительно стационарной траектории будет выглядеть следующим образом [1, c. 302]:
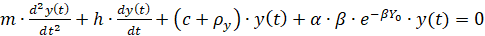(1)
где m – приведенная масса подсистемы режущего инструмента к резцу,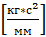 
;
h – приведенная диссипация подсистемы инструмента,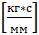 
;
c – приведенный коэффициент жесткости подсистемы инструмента,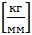 
; ρy - жесткость процесса резания 
;
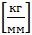y(t) – упругое деформационное смещение резца относительно заготовки в радиальном направлении, мм;
α, β – коэффициенты, определяющие вид нелинейной статической характеристики.
Потеря системой резания работоспособности в терминах теории автоматического управления характеризуется потерей системой устойчивости. Поэтому важно выявить основные пути потери устойчивости системой, связать их с параметрами системы [2, c. 29].
Выполним анализ принципиального влияния параметров системы на её устойчивость в процессе её работы, то есть в процессе резания, в принятой схематизации.
Если рассмотреть линеаризованное дифференциальное уравнение динамики процесса точения (1), то можно сделать ряд выводов.
Во-первых, на устойчивость системы будут оказывать отношения значений численных величин параметров системы.
Во-вторых, на устойчивость технологической системы влияют параметры, которые изменяются достаточно быстро в пределах одного технологического прохода. К таким параметрам можно отнести жёсткость процесса резания ρy и коэффициент β – параметр крутизны нарастания характеристики контактного взаимодействия двух поверхностей [3, c. 150].
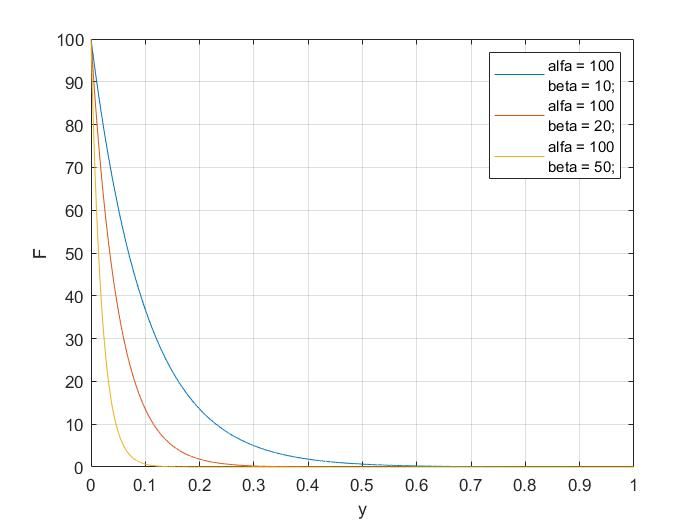
На рисунке 2 (а) показано, как значение параметра β влияет на крутизну нарастания характеристики контактного взаимодействия двух поверхностей.
а)
б)
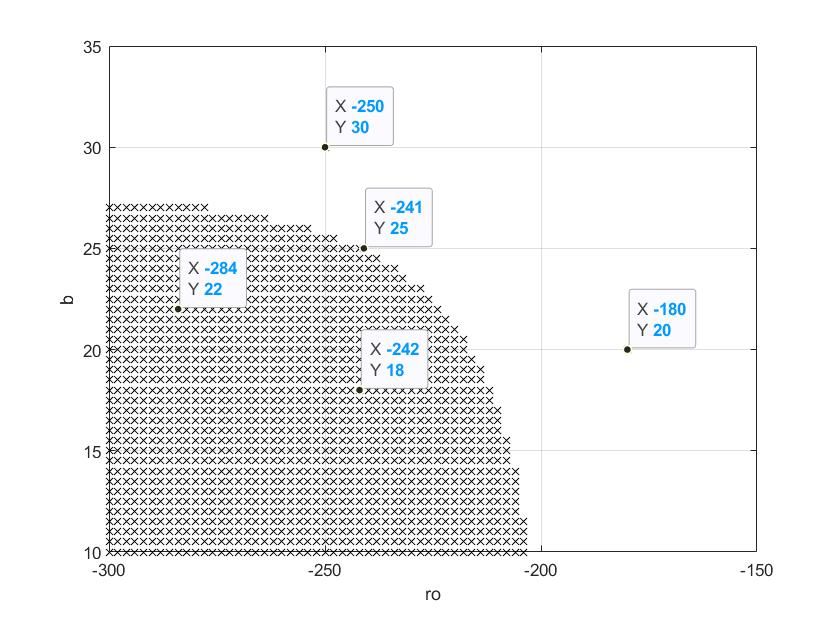
Рис. 2. Динамические характеристики системы: а) характеристика силы контактного взаимодействия; б) Области устойчивых и неустойчивых движений системы (знак х – неустойчивая траектория движения)
Жёсткость процесса резания ρy и параметр β определяются физико-химическими процессами, протекающими в зоне резания, и являются неуправляемым и трудно измеримыми параметрами.
Таким образом, в первую очередь, необходимо выполнить исследование влияния соотношения значений пар параметров ρy и β на устойчивость технологической системы.
Выполнив аналитико-численный анализ устойчивости системы при различных значениях варьируемых параметров ρy и β, получили следующие области устойчивых и неустойчивых движений, которые представлены на рисунке 2 (б), где (x) – неустойчивые движения системы.
Таким образом, полученные области устойчивых и неустойчивых траекторий движений показывают, что имеются такие значения пар параметров системы ρy и β при которых система теряет устойчивость. Для повышения надежности работоспособности системы точения рекомендуется использовать систему диагностирования текущего динамического состояния процесса точения, которая должна прогнозировать скорую потерю устойчивости системой и передавать прогноз системе автоматического управления процессом точения.
.png&w=640&q=75)
