Одним из вопросов методики преподавания математики является вопрос формирования у учащихся умений и навыков решения текстовых задач. Задачи являются материалом для ознакомления учащихся с новыми понятиями, для развития логического мышления, формирования межпредметных связей. Задачи позволяют применять знания, полученные при изучении математики, при решении практических вопросов, которые возникают в жизни человека. Этапы решения задач являются формами развития мыслительной деятельности.
Текстовой задачей обычно называют взаимосвязанный краткий рассказ, в котором присутствуют некоторые данные и ставится задача найти другие неизвестные данные, связанные между собой определенными отношениями, приведенными в условии [8, с.20]. Текстовая задача состоит из двух частей: условия и требования. В условии сообщаются сведения об объектах и величинах, характеризующих данные объекты, об известных и неизвестных значениях этих величин, об отношениях между ними. Требование задачи ‒ это указание того, что нужно найти. Оно может быть выражено предложением в повелительной или вопросительной форме.
Типизация тестовых задач на целые числа разнообразна. По моему мнению, задачи можно разделить на 3 вида:
- задачи, в которых данные заданы в множестве целых значений;
- задачи, в которых ответ задачи получен в множестве целых значений;
- задачи, в которых и данные и ответ заданы в множестве целых значений.
Понятие «решение задачи» часто используется в математике. Этот термин обозначает связанные между собой, но все же разные понятия:
- решение задачи – это процесс поиска этого результата, то есть все действия с момента начала чтения задачи до окончания решения;
- решение задачи – это результат, то есть ответ на поставленный вопрос задачи;
- решение задачи – это лишь та деятельность человека, решающего задачу, которую он производит над условием задачи и их следствиями на основе общих положений математики для получения результата [8, с.21-22].
Решение задачи подразумевает раскрытие связи между данными, указанными в условии задачи, и искомыми величинами, сформулировать цепочку использования общих положений математики (формул, законов, правил, и т.д.), выполнить действия над данными задачи с использованием общих положений, указанных выше. Последним этапом является получение ответа на вопрос задачи или доказательство невозможности его выполнения.
Процесс решения задач будем рассматривать как сложный аналитико-синтетический процесс направленного взаимодействия субъекта с объективным содержанием решаемой задачи.
Важным научным и методическим условием реализации концепции компетентностного подхода при обучении математике является обучение школьников моделированию, что имеет важное значение для формирования мировоззрения обучаемых, поскольку естественным этапом развития познания, на котором осуществляется переход от содержательного и качественного анализа объекта к формализации и количественному анализу, является математическое моделирование реальных процессов.
Моделирование - общенаучный метод познания действительности, при котором для исследования объекта строится его модель, сохраняющая основные, выделенные особенности объекта исследования [1, с. 52-53].
Модели делят на две группы по видам средств, которые используются для их построения: знаковые и схематизированные [6, c. 2].
Решающими моделями называют знаковые модели текстовых задач, реализованные на математическом языке. Именно они применяются в решении задач. Оставшиеся модели – это вспомогательные модели, с помощью которых осуществляется переход от текста задачи к её математической модели.
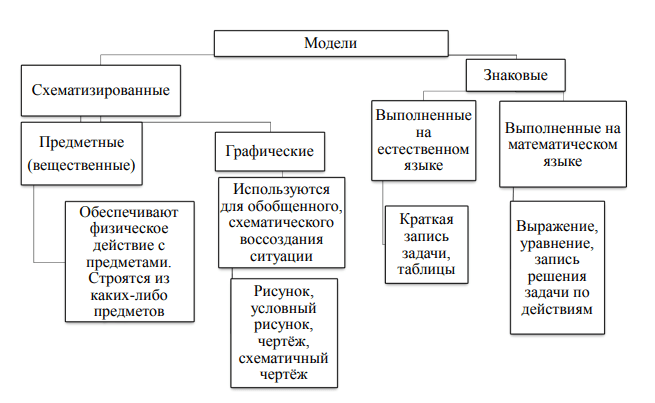
Рис. 1. Основные виды моделей
Покажем это на примере решения задачи с использованием знаковой и схематизированной модели.
«В одном вагоне электропоезда было пассажиров в 2 раза больше, чем в другом. Когда из первого вагона вышли 3 человека, а во второй вагон вошли 7 человек, то в обоих вагонах пассажиров стало поровну. Сколько пассажиров было в каждом вагоне первоначально?» [2, c. 200].
Обозначим через х первоначальное количество пассажиров во втором вагоне. Значит количество пассажиров в первом вагоне ‒ 2∙х. Как только первый вагон покинули 3 человека, оставшееся количество человек составило 2∙х – 3. Во второй вагон зашли 7 пассажиров, следовательно, теперь в нем х+7 человек. Поскольку теперь и тот и другой вагон имеет равное количество пассажиров, то их можно приравнять – 2∙х ‒ 3=х+7. Полученное уравнение и есть математическая модель данной задачи.
Второй этап ‒ решение получившегося уравнения.
Последний этап ‒ использование полученного решения, с целью ответа на вопрос задачи: во втором вагоне первоначально было 10 пассажиров, а 20 (10 ∙ 2=20) пассажиров – в первом.
В процессе решения текстовой задачи наибольшую трудность для учащегося представляет собой переход от естественного языка на математический. Для облегчения этого этапа используют вспомогательные модели ‒ рисунки, таблицы, схемы и другие. В этом случае процесс решения задачи рассматривают как переход от одного вида модели к другому: от модели, представленной на естественном языке, к вспомогательной (рисунки, таблицы схемы, и т.д.). Далее происходит переход от вспомогательной модели к математической, в процессе которой происходит решение задачи.
Приемы моделирования состоят из исследований того или иного объекта (текстовой задачи), подбирают и используют другой объект, в каком-либо отношении подобный тому, который исследуют. Новый объект изучают, с его помощью решают исследование задачи, а-затем результат переносят на первоначальный объект.
Покажем виды графических моделей на примере простейшей задачи [9, c. 255-257]: «Лида нарисовала 4 домика, а Вова на 3 домика больше. Сколько домиков нарисовал Вова?»
1) рисунок;

Рис. 2. Первый вид графической модели
2) условный рисунок;
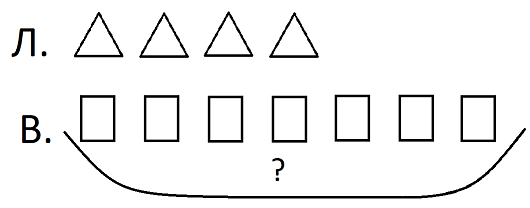
Рис. 3. Второй вид графической модели
3) чертеж;
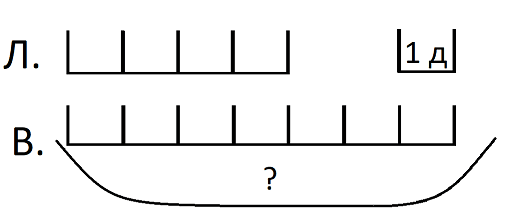
Рис. 4. Третий вид графической модели
4) символический чертеж(схема).
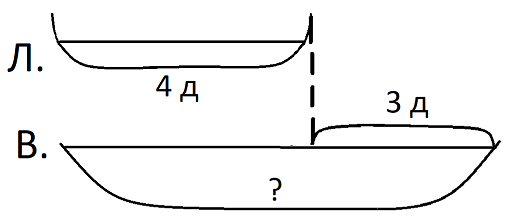
Рис. 5. Четвертый вид графической модели
Знаковые модели используют в выполнении на естественном и на математическом языке. К знаковой модели, которая выполнена на естественном языке, можно отнести краткую запись задачи.
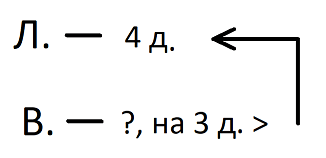
Рис. 6. Краткая запись
К знаковым моделям текстовых задач, которые выполнены на математическом языке, относят [4, c.12]:
- выражение, уравнение, запись решения задачи по действиям;
- решающие модели (решение задачи);
- вспомогательные модели – это знаковые модели, которые выполнены на естественном языке;
- переход от текста задачи к математической модели.
Не каждый чертеж или краткая запись, которые выполнены для данной задачи, называют ее моделями. Поскольку модель ‒ это схематичная копия задачи, то в ней должны присутствовать все существенные признаки: указаны требования и отношения между данными и искомыми элементами.
Изучим процесс решения арифметическим методом текстовой задачи о пассажирах в двух вагонах.
Анализ задачи позволяет предварительно вычленить ее объекты. Ими являются пассажиры в двух вагонах поезда. Из условия задачи известно, что:
- в первом вагоне в 2 раза больше человек, чем во втором;
- первый вагон покинули 3 человека;
- второй вагон увеличился на 7 человек;
- в первом и втором вагонах стало равное количество пассажиров.
В результате задачи необходимо выяснить «сколько человек было изначально в первом и во втором вагонах?».
Далее построим графическую модель данной задачи в виде схематического чертежа.
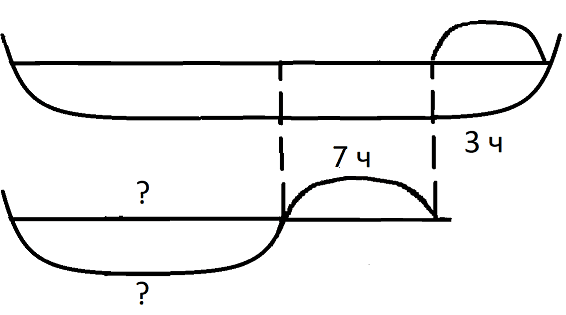
Рис. 7. Графическая модель
Из чертежа видно, что математическая модель задачи имеет вид:
- Число пассажиров во втором вагоне – 7+3.
- Число пассажиров в первом вагоне – (7+3) ∙ 2.
Произведя простейшие вычисления, определили ответ на вопрос задачи: во втором вагоне было 10 человек, а в первом ‒ 20 человек.
Выделим основные умения, которыми должен владеть обучаемый [3, c. 23-24]:
- умение анализировать текст задачи, выделять вопрос задачи и существенные условия для ее решения;
- определять вид задачи и использовать в ее решении определенный вид графической интерпретации;
- выполнять эквивалентные преобразования условия задачи;
- производить адекватный перевод условия задачи на язык выбранной модели (символический, графический) и обратный перевод (интерпретация результатов).
Общая характеристика задач сводится к рассмотрению задачи как субъективного, психологического отражения внешней ситуации, в которой развертывается целенаправленная деятельность субъекта. Процесс решения задач будем рассматривать как сложный аналитико-синтетический процесс направленного взаимодействия субъекта с объективным содержанием решаемой задачи.
В ходе работы с графическими моделями мы убедились, что они являются эффективным средством поиска решения задачи. В процессе решения учащимся приходится переходить от одной формы записи к другой и находить среди них оптимальную. Процесс графического моделирования текстовой задачи повышает мыслительную активность учащихся, способствует развитию вариативности мышления, а значит, делает решение задач более приятным и интересным.
Чтобы самостоятельно решать задачи, ученик должен освоить различные виды моделей, научиться выбирать модель, соответствующую предложенной задаче, и переходить от одной модели к другой. Для того чтобы вооружить учащихся моделированием как способом познания, нужно, чтобы школьники сами строили модели, сами изучали какие-либо объекты, явления с помощью моделирования.
Использование графического моделирования при решении текстовых задач обеспечит более качественный анализ задачи, осознанный поиск ее решения, обоснованный выбор арифметических действий и предупредит многие ошибки в решении задач. Модель задачи может быть использована для составления и решения обратных задач [10, c.4-5].
Таким образом, обучение с применением графического моделирования повышает активность мыслительной деятельности учащихся; помогает понять задачу; осознать выбор действия; найти самостоятельно рациональный путь решения, установить способ проверки.
Вывод: в целом полученные результаты дают основание предположить, что опыт работы по графическому моделированию текстовых задач на уроках математики имеет практическую значимость для повышения качества образовательного процесса. И наша работа имеет конкретную учебную направленность и может быть использована в практической деятельности другими педагогами.

.png&w=640&q=75)