Оценка моделей нейронных сетей в простой задаче классификации

Введение

Нейронные сети (НС) – мощный инструмент обработки и анализа данных, который позволяет решать задачи кластеризации и классификации, прогнозирования, генерации изображений и текста и многие другие. Существует множество моделей нейронных сетей, которые созданы специально под определённый класс задач: свёрточные нейронные сети для классификации изображений, рекуррентные – для задач с временной характеристикой, например анализ непрерывного текста или звука. Но, также нейронные сети являются универсальными и могут решать различный круг задач с несколько меньшей эффективностью [1].

В работе будут рассмотрены 3 модели нейронных сетей: многослойный персептрон, свёрточная и рекуррентная нейронные сети в задаче классификации изображений рукописных цифр (набор данных MNIST).

Описание моделей НС

Персептрон смоделирован следующим образом: входной слой представляет собой набор из нейронов в количестве соответствующим размерности одномерного вектора, полученному из последовательности пикселей изображения. Первый скрытый слой состоит из 2048 нейронов, второй – из 1024 с функциями активации ReLU. Выходной слой имеет 10 нейронов по числу классов изображения (цифры от 0 до 9). На последнем слое используется функция активации SoftMax.

Свёрточная нейронная сеть (СНС) позволяет выделить самые важные не только пиксели изображения, но и более абстрактные структуры, такие как линии или области и имеет более сложную структуру [2]. В примере будет использована сеть со следующей архитектурой: первый слой СНС – свёрточный с фильтром 3 на 3 пикселя с добавлением пустой строки и столбца, благодаря чему конечный размер изображения будет совпадать с изначальным. Изображение разбивается на 32 карты признаков, далее происходит операция MaxPooling, с матрицей 2 на 2 пикселя, которая позволяет выявить самые значимые пиксели в каждой области размерностью 2 на 2. Таким образом, изображение сжимается в 2 раза. Следующим этапом приведённые операции повторяются ещё раз, но с использованием 64 фильтров на свёрточном слое. В итоге, полученное изображение и переведённое в одномерный вектор, подаётся на вход персептрону с 1 скрытым слоем из 128 нейронов и выходной имеет также 10 нейронов – по числу классов изображений.

Рекуррентная нейронная сеть (РНС), может запоминать состояния системы и обрабатывает новые данные исходя из информации, полученной ранее, именно поэтому они лучше всего подходят для задач прогнозирования и классификации потоковых данных [4]. Структура рассмотренной РНС: входной слой аналогично с входом на персептрон, далее идёт рекуррентный слой со 128 нейронами, выход – 10 элементов.

Во всех моделях использовалась функция ошибки «категориальная кроссэнтропия», оптимизатор обучения Адама.

Подготовка набора данных

Для корректной обработки массива данных, их необходимо нормализовать. Набор данных MNIST содержит 50000 изображений в градациях серого размеров 28 на 28 пикселей. Один цветовой канал означает характеристику пикселя как интенсивность цвета, 0 (чёрный) до 255 (белый). Поэтому уместно разделить значение пикселя на 255, диапазон значений будет в пределах от 0 до 1.

Данные о правильных ответах выборки были нормализованы с помощью технологии «One Hot Encoding» и превращены в вектора вида [1,0,0,0,0,0,0,0,0,0], где порядковый номер единицы означает класс изображения [3].

Результаты исследования

Каждая модель сети была обучена на 5 эпохах, на вход поступали батчи из 32 изображений. Исследование выполнялось на фреймворке Keras, языке программирования Python. Графики обучения представлены ниже (рис. 1-3).

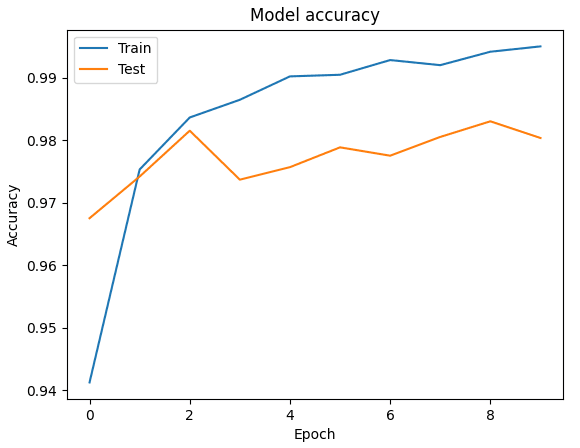
Рис. 1. График точности обучения персептрона

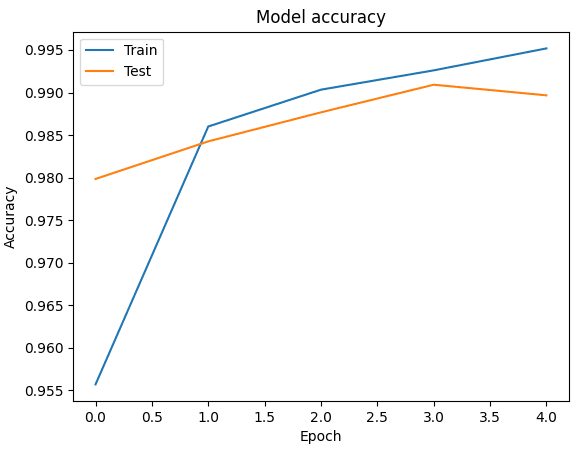
Рис. 2. График точности обучения СНС

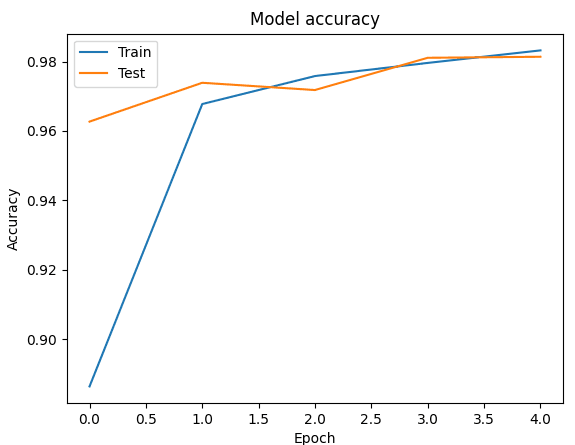
Рис. 3. График точности обучения РНС

Получена сравнительная таблица эффективности обучения нейронных сетей.

Таблица

Сравнение эффективности моделей НС

Исходя из таблицы, можно сделать вывод о том, что лучшей моделью в данной задаче оказалась свёрточная нейронная сеть, со значением точности на тестовой выборке 98,9. Минусом данной модели оказывается время обучения, на 5 итераций было затрачено 121 секунда (значения округлены до целых), соответственно, рекуррентной НС на обучение понадобилось 53 секунды. Худшей в задаче классификации рукописных цифр оказалась модель персептрона с большим временем обучения (113 секунд), что связано с большим количеством нейронов в скрытых слоях, и худшим значением на тестовом наборе данных. РНС имеет наименьший разброс в значениях обучающей и тестовой выборки.