Введение. За последние годы выросло число экспериментальных и теоретических публикаций, связанных с получением молекул при низких температурах с помощью методики фотоассоциации холодных атомов [1-3]. Важность этих исследований вызвана изучением динамики столкновения холодных частиц и проведением химических реакций при низких температурах. Для синтеза холодных молекул необходимы данные о радиационных параметрах молекул.
В работах [4-13] были рассчитаны энергетические и радиационные параметры, а также радиационные времена жизни возбужденных состояний электронных переходов 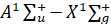 и
и 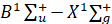 гомо и гетероядерных димеров атомов щелочных металлов (Li2, Na2,, K2, Rb2, Cs2, NaK, NaRb, NaCs, KLi, KRb, CsRb, CsLi,). Расчеты проводились квантово-химическим методом на основе полуэмпирических потенциальных кривых. Сравнение результатов расчета с экспериментальными данными показало эффективность метода расчета. В настоящей работе проведены расчеты радиационных параметров
гомо и гетероядерных димеров атомов щелочных металлов (Li2, Na2,, K2, Rb2, Cs2, NaK, NaRb, NaCs, KLi, KRb, CsRb, CsLi,). Расчеты проводились квантово-химическим методом на основе полуэмпирических потенциальных кривых. Сравнение результатов расчета с экспериментальными данными показало эффективность метода расчета. В настоящей работе проведены расчеты радиационных параметров 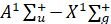 электронного перехода димера кальция. Спектральный анализ электронного перехода
электронного перехода димера кальция. Спектральный анализ электронного перехода 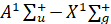 молекулы Ca2 проводился в ряде работ с использованием лазерных методик и техники высокого разрешения [14-17]. Были получены молекулярные постоянные для основного и возбужденного электронных состояний. В отличие от димеров атомов щелочных металлов основные электронные состояния щелочноземельных димеров являются слабосвязанными. В работе [18] отмечается, что димеры щелочноземельных металлов являются кандидатами для создания газовых лазеров.
молекулы Ca2 проводился в ряде работ с использованием лазерных методик и техники высокого разрешения [14-17]. Были получены молекулярные постоянные для основного и возбужденного электронных состояний. В отличие от димеров атомов щелочных металлов основные электронные состояния щелочноземельных димеров являются слабосвязанными. В работе [18] отмечается, что димеры щелочноземельных металлов являются кандидатами для создания газовых лазеров.
Построение потенциальных кривых. Для построения потенциальных кривых нами использовалась модель потенциальной кривой возмущенного осциллятора Морзе (ВОМ) [19, 20]:
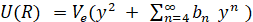 (1)
(1)
где y = 1 – exp[–α(R– Re)], Re – равновесное межъядерное расстояние; Ve, α, и bn – параметры потенциальной функции ВОМ.
В работах [21, 22] на основе потенциальных функций ВОМ для молекул Cu2, Ag2, Au2, Na2, K2, Cs2 были рассчитаны молекулярные постоянные и проведено сравнение с экспериментальными данными. В таблице 1 приведены рассчитанные параметры потенциальных кривых ВОМ для основного и возбужденного электронных состояний димера кальция. Для расчета параметров ВОМ использовались экспериментальные молекулярные постоянные работы [12]. На рисунке приведены построенные потенциальные кривые для основного и возбужденного электронных состояний димера кальция.
Таблица 1
Параметры потенциальных кривых ВОМ для основного и возбужденного состояний электронного перехода 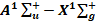 димера кальция
димера кальция
|
|
| ||
|---|---|---|---|
|
Ve, cм-1 |
1004.53 |
|
8693.6 |
|
α, Å -1 |
1.117 |
|
0.787 |
|
Re, Å |
4.279 |
|
3.807 |
|
b4 |
-0.0212045393 |
b4 |
-2.53606299310 |
|
b5 |
0.0568882660 |
b5 |
0.348369528240 |
|
b6 |
-0.0201475322 |
b6 |
0.067330369122 |
|
b7 |
0.0083492971 |
b7 |
0.682550219251 |
|
b8 |
0.0126459810 |
b8 |
-1.374438273835 |
|
b9 |
-0.0039382965 |
b9 |
-2.633138916950 |
|
b10 |
0.0096507732 |
b10 |
2.069553134350 |
|
b11 |
0.0013671888 |
b11 |
5.311839823195 |
|
b12 |
0.0032528726 |
b12 |
3.2534671555975 |
|
b13 |
0.0029313968 |
b13 |
-13.077148709884 |
|
b14 |
0.0023054645 |
b14 |
-10.460504960207 |
|
b15 |
0.0016304892 |
b15 |
37.716119412386 |
|
b16 |
0.0024581377 |
b16 |
-33.195675734845 |
|
b17 |
0.0010259461 |
b17 |
-74.317441869381 |
|
b18 |
0.0019361204 |
b18 |
154.429899061148 |
|
b19 |
0.0010577249 |
b19 |
85.8562198465453 |
|
b20 |
0.0013994146 |
b20 |
523.924651742465 |
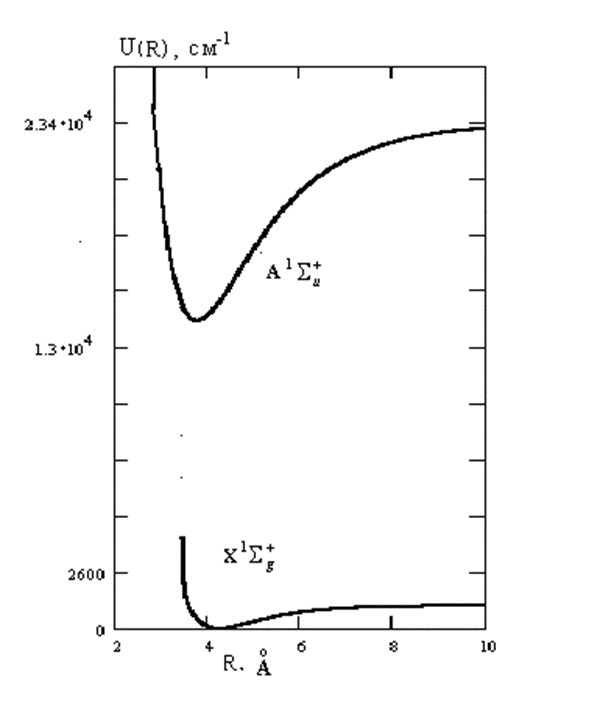
Рис. Потенциальные кривые ВОМ основного и возбужденного состояний электронного перехода  молекулы Ca2
молекулы Ca2
Для проверки надежности построенных потенциальных кривых на их основе были рассчитаны колебательные энергии Ev, и вращательные постоянные Bv и проведено сравнение с экспериментальными данными. Колебательные энергии и соответствующие им волновые функции колебательного уравнения Шредингера были рассчитаны методом Нумерова – Кулея [23]. Уравнение Шредингера имеет вид:
 (2)
(2)
Рассчитанные волновые функции использовались для получения вращательных постоянных по соотношению теории возмущений для модели вращающегося осциллятора двухатомной молекулы [24]:
 (3)
(3)
где матричный элемент 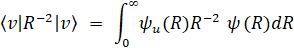 , b = h/8p2cμ, μ – приведенная масса атомов молекулы, h – постоянная Планка, с – скорость света.
, b = h/8p2cμ, μ – приведенная масса атомов молекулы, h – постоянная Планка, с – скорость света.
Рассчитанные значения молекулярных постоянных Ev и Bv для основного и возбужденного электронных состояний приведены в таблице 2.
Таблица 2
Результаты расчета колебательных энергий Ev и вращательных постоянных Bv (в см-1) на основе потенциальных кривых для основного возбужденного состояния электронного перехода 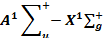 молекулы Ca2
молекулы Ca2
|
v |
Ev |
Bv |
Ev |
Bv |
|
X |
A | |||
|
0 |
32.23 |
0.0456 |
68.08 |
0.0593 |
|
1 |
95.11 |
0.0449 |
203.23 |
0.0585 |
|
2 |
155.88 |
0.0441 |
336.90 |
0.0580 |
|
3 |
214.55 |
0.0433 |
469.07 |
0.0576 |
|
4 |
271.13 |
0.0426 |
599.71 |
0.0572 |
|
5 |
325.60 |
0.0418 |
728.79 |
0.0568 |
|
6 |
377.87 |
0.0409 |
856.29 |
0.0565 |
|
7 |
428.24 |
0.0401 |
982.18 |
0.0561 |
|
8 |
476.40 |
0.0393 |
1106.42 |
0.0557 |
|
9 |
522.47 |
0.0384 |
1228.98 |
0.0552 |
|
10 |
566.43 |
0.0375 |
1349.84 |
0.0548 |
|
11 |
608.29 |
0.0366 |
1468.94 |
0.0544 |
|
12 |
648.05 |
0.0357 |
1586.27 |
0.0539 |
|
13 |
685.71 |
0.0347 |
1701.79 |
0.0535 |
|
14 |
721.27 |
0.0338 |
1815.45 |
0.0530 |
|
15 |
754.72 |
0.0325 |
1927.22 |
0.0526 |
Рассчитанные колебательные энергии и вращательные постоянные связаны с фундаментальными колебательными и вращательными молекулярными постоянными соотношениями:
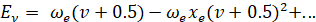 , (4)
, (4)
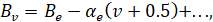 (5)
(5)
В таблице 3 приведено сравнение экспериментальных и рассчитанных по соотношениям (4) и (5) колебательных и вращательных молекулярных постоянных.
Таблица 3
Сравнение результатов расчета колебательных и вращательных молекулярных постоянных (см-1) с экспериментальными данными для основного и возбужденного электронных состояний электронного перехода  димера кальция
димера кальция
|
Молекулярные постоянные | 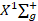 | 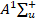 |
|---|---|---|
|
we |
64.98 65.07 |
136.61 136.65 |
|
wexe |
-1.071 -1.087 |
-0.723 -0.721 |
|
weye |
3.38(-3) 3.46(-3) |
- 2.79(-3) - 2.85(-3) |
|
Be |
4.60(-2) 4.61(-2) |
5.80(-2) 5.82(-2) |
|
ae |
-7.37(-4) -7.41(-4) |
-2.95(-4) -2.97(-4) |
Примечание. 1-я строка – результаты расчета на основе потенциальных кривых; 2-я строка – экспериментальные данные [17].
Радиационные параметры. К радиационным параметрам молекул относятся коэффициенты Эйнштейна для спонтанного излучения 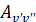 , cилы осциллятора
, cилы осциллятора 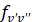 , факторы Франка-Кондона (ФФК)
, факторы Франка-Кондона (ФФК) 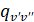 , волновые числа электронно-колебательных полос
, волновые числа электронно-колебательных полос 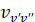 .
.
Коэффициент Эйнштейна (с-1) и сила осциллятора для поглощения (безразмерная величина) связаны с функцией дипольного момента электронного перехода от межъядерного расстояния (ат. ед.) соотношениями [25]:
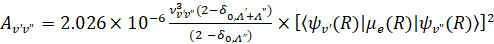 (6)
(6)
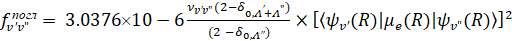 , (7)
, (7)
где Λ – проекция орбитального момента количества движения электронов на межъядерную ось (Λ = 0, 1, 2,… для состояний Σ, Π, Δ,...); δ0,Λ символ Кронекера, равный 1, если Λ = 0 и нулю для других значений Λ; 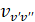 – волновое число электронно-колебательного перехода;
– волновое число электронно-колебательного перехода; 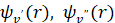 – колебательные волновые функции возбужденного и основного электронных состояний.
– колебательные волновые функции возбужденного и основного электронных состояний.
ФФК характеризуют относительное распределение интенсивностей электронно-колебательных полос и представляют собой квадраты интеграла перекрывания колебательных волновых функций комбинирующих электронных состояний
 . (8)
. (8)
Для расчета волновых чисел колебательных полос электронного перехода 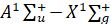 использовалось выражение
использовалось выражение
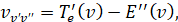 (9)
(9)
где 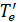 – электронная энергия возбужденного состояния;
– электронная энергия возбужденного состояния;  – колебательные энергии для возбужденного и основного электронных состояний.
– колебательные энергии для возбужденного и основного электронных состояний.
Были рассчитаны радиационные параметры для электронного перехода 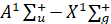 молекулы Ca2 (0 ≤ v′ ≤ 18, 0 ≤ v′′ ≤ 15. Из-за громоздкости рассчитанного массива радиационных параметров в таблице 4 приведена часть полученных результатов.
молекулы Ca2 (0 ≤ v′ ≤ 18, 0 ≤ v′′ ≤ 15. Из-за громоздкости рассчитанного массива радиационных параметров в таблице 4 приведена часть полученных результатов.
Таблица 4
Результаты расчета радиационных параметров электронного перехода молекулы Сa2
|
v'' |
v’ = 0 |
v’ = 1 |
v' = 2 |
v' = 3 |
v' = 4 |
v' = 5 |
v' = 6 |
v' = 7 |
v' = 8 |
|---|---|---|---|---|---|---|---|---|---|
|
0 |
0.00151 1.13(+5) 8.31(-4) 14286.7 |
0.00852 6.52(+6) 4.70(-3) 14422.6 |
0.02515 1.96(+6) 1.39(-2) 14558.5 |
0.05152 4.10(+6) 2.85(-2) 14693.7 |
0.08241 6.69(+6) 4.56(-2) 14828.5 |
0.10970 9.08(+6) 6.08(-2) 14962.8 |
0.12650 1.07(+7) 7.03(-2) 15096.7 |
0.12984 1.12(+7) 7.24(-2) 15230.1 |
0.12096 1.06(+7) 6.76(-2) 15366.2 |
|
1 |
0.00754 5.61(+5) 4.61(+5) 14223.9 |
0.03272 2.48(+6) 1.80(-2) 14360.0 |
0.02515 5.47(+6) 3.90(-2) 14495.6 |
0.09978 7.86(+6) 5.50(-2) 14630.8 |
0.10010 8.04(+6) 5.53(-2) 14765.6 |
0.07181 5.88(+6) 3.97(-2) 14899.8 |
0.03323 2.78(+6) 1.84(-2) 15033.8 |
0.00585 4.99(+5) 3.25(-3) 15167.2 |
0.00102 8.91(+4) 5.71(-4) 15300.3 |
|
2 |
0.02020 1.49(+6) 1.11(-2) 14163.2 |
0.06524 4.90(+6) 3.59(-2) 14299.1 |
0.09676 7.41(+6) 5.33(-2) 14434.9 |
0.08075 6.30(+6) 4.45(-2) 14570.5 |
0.03413 2.71(+6) 1.88(-2) 14704.0 |
0.00217 1.75(+5) 1.19(-3) 14838.1 |
0.00808 6.71(+5) 4.49(-3) 14973.0 |
0.03680 3.12(+6) 2.05(-2) 15106.5 |
0.05829 5.03(+6) 3.25(-2) 15239.5 |
|
3 |
0.03853 2.82(+6) 2.12(-2) 14104.6 |
0.08906 6.64(+6) 4.91(-2) 14240.6 |
0.08105 6.15(+6) 4.46(-2) 14376.2 |
0.02685 2.07(+6) 1.48(-2) 14510.9 |
0.00002 1.32(+3) 1.34(-5) 14645.5 |
0.02284 1.84(+6) 1.26(-2) 14779.6 |
0.05132 4.27(+6) 2.84(-2) 14914.3 |
0.04710 3.95(+6) 2.61(-2) 15047.6 |
0.01928 1.65(+6) 1.07(-2) 15180.4 |
|
4 |
0.05882 4.27(+6) 3.24(-2) 14048.0 |
0.09240 6.93(+6) 5.09(-2) 14184.1 |
0.04137 3.11(+6) 2.27(-2) 14319.6 |
0.00018 1.37(+4) 9.83(-5) 14454.9 |
0.02406 1.88(+6) 1.33(-2) 14589.6 |
0.05068 4.05(+6) 2.80(-2) 14723.9 |
0.03305 2.69(+6) 1.83(-2) 14857.9 |
0.00394 3.26(+5) 2.18(-3) 14991.2 |
0.00523 4.45(+5) 2.92(-3) 15124.0 |
|
5 |
0.07668 5.52(+6) 4.23(-2) 13993.2 |
0.07604 5.58(+6) 4.19(-2) 14129.6 |
0.00902 6.71(+5) 4.94(-3) 14265.5 |
0.01323 1.01(+6) 7.31(-3) 14400.4 |
0.04768 3.70(+6) 2.63(-2) 14534.9 |
0.03073 2.43(+6) 1.69(-2) 14669.5 |
0.00136 1.09(+6) 7.45(-4) 14803.3 |
0.01180 9.75(+5) 6.55(-3) 14936.8 |
0.03601 3.03(+6) 2.00(-2) 15068.9 |
|
6 |
0.08885 6.36(+6) 4.90(-2) 13941.2 |
0.04973 3.62(+6) 2.74(-2) 14077.8 |
0.00019 1.48(+4) 1.10(-4) 14212.8 |
0.03720 2.82+6) 2.05(-2) 14348.0 |
0.03836 2.95(+6) 2.11(-2) 14482.7 |
0.00334 2.61(+5) 1.83(-3) 14617.1 |
0.01090 8.76(+5) 6.04(-2) 14750.3 |
0.03538 2.89(+6) 1.96(-2) 14884.4 |
0.02519 2.10(+6) 1.40(-2) 15016.9 |
|
7 |
0.09411 6.68(+6) 5.19(-2) 13890.2 |
0.02452 1.77(+6) 1.35(-2) 14026.6 |
0.01087 8.04(+5) 6.01(-3) 14162.5 |
0.04589 3.45(+6) 2.53(-2) 14297.6 |
0.01375 1.05(+6) 7.55(-3) 14432.4 |
0.00410 3.22(+5) 2.27(-3) 14566.7 |
0.03180 2.53(+6) 1.76(-2) 14700.9 |
0.02508 2.03(+6) 1.39(-2) 14834.2 |
0.00147 1.21(+5) 8.10(-4) 14967.0 |
|
8 |
0.09296 6.56(+6) 5.13(-2) 13842.4 |
0.00744 5.34(+5) 4.10(-3) 1398056 |
0.02777 2.04(+6) 1.53(-2) 14117.1 |
0.03572 2.66(+6) 1.96(-2) 14249.3 |
0.00036 2.65(+4) 1.92(-4) 14384.0 |
0.02188 1.70(+6) 1.21(-2) 14518.4 |
0.02995 2.36(+6) 1.65(-2) 14652.3 |
0.00383 3.07(+5) 2.11(-3) 14785.6 |
0.00716 5.91(+5) 3.98(-3) 14918.7 |
Примечание. Первая строка – 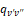 ; вторая строка –
; вторая строка – 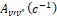 ; третья строка –
; третья строка – 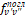 (безразмерная величина); четвертая строка –
(безразмерная величина); четвертая строка – 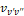 (см-1).
(см-1).
Выводы. Расчет радиационных параметров  ,
,  ,
, 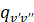 ,
,  , проведен с использованием потенциальных кривых, построенных в данной работе. Надежность потенциальных кривых подтверждена хорошо согласующимися спектроскопическими молекулярными постоянными, рассчитанными на основе потенциальных кривых и экспериментальными данными. При расчетах значений
, проведен с использованием потенциальных кривых, построенных в данной работе. Надежность потенциальных кривых подтверждена хорошо согласующимися спектроскопическими молекулярными постоянными, рассчитанными на основе потенциальных кривых и экспериментальными данными. При расчетах значений 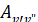 и
и  использована зависимость дипольного момента электронного перехода
использована зависимость дипольного момента электронного перехода 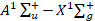 от межъядерного расстояния μe(R) электронного перехода
от межъядерного расстояния μe(R) электронного перехода 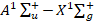 для молекулы Ca2, полученная в работе [14]. Радиационные параметры рассчитаны впервые. Результаты расчета коэффициентов Эйнштейна, факторов Франка-Кондона и волновых чисел колебательных полос могут найти применение при создании газового лазера на электронном переходе
для молекулы Ca2, полученная в работе [14]. Радиационные параметры рассчитаны впервые. Результаты расчета коэффициентов Эйнштейна, факторов Франка-Кондона и волновых чисел колебательных полос могут найти применение при создании газового лазера на электронном переходе 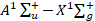 димера кальция и пополнения банка данных по радиационным параметрам молекул.
димера кальция и пополнения банка данных по радиационным параметрам молекул.

 молекулы Ca2 (0 ≤ v′ ≤ 18, 0 ≤ v′′ ≤ 15). Расчеты выполнены квантово-химическим методом. Решение волнового уравнения Шредингера проведено на основе потенциальных кривых возмущенного осциллятора Морзе, построенных в данной работе.
молекулы Ca2 (0 ≤ v′ ≤ 18, 0 ≤ v′′ ≤ 15). Расчеты выполнены квантово-химическим методом. Решение волнового уравнения Шредингера проведено на основе потенциальных кривых возмущенного осциллятора Морзе, построенных в данной работе.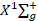

.png&w=640&q=75)