Вспомним определение линейного уравнения. Уравнение вида ax=b, где x переменная a и b некоторые числа называется линейным уравнением с одной переменной.
Рассмотрим три случая решения линейного уравнения fp=x∙g(p).
Первый случай, когда f(p) и g(p), равны нулю, тогда уравнение имеет бесконечное число решений; если f(p) равно нулю, а g(p) не равно нулю, то уравнение не имеет решений; если f(p) не равен нулю, g(p) принимает любые значения, то уравнение имеет единственное решение.
Рассмотрим пример решения уравнения с помощью двух моделей (аналитическая и геометрическая).
Задание. При каких значениях параметра p уравнение
p(p-3)x+p=0
имеет бесконечное множество корней?
Аналитическое решение. При p=3 уравнение p(p-3)x+p=0 принимает вид 0∙x+3=0. Уравнение корней не имеет. При p=0 уравнение p(p-3)x+p=0 принимает вид 0∙x+0=0. Уравнение имеет бесконечное число корней. При p≠3 и p≠0 уравнение p(p-3)x+p=0 имеет единственный корень 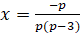 .
.
Таблица
Случаи решения уравнения
|
p=3 |
0∙x+3=0 |
корней нет |
|
p=0 |
0∙x=0 |
бесконечное число корней |
|
p≠0 и p≠3 |
p(p-3)x=-p |
единственный корень |
Геометрическое представление решений заданий с параметрами посредством системы GeoGebra дает возможность просмотреть расположения функций при различных значениях параметров и не упустить частные решения таких заданий.
GeoGebra имеет важный инструмент ползунок, позволяющий изменять величины, которые используются для построения объекта (величину угла, длину отрезка, коэффициент в алгебраическом описании объекта). Данный инструмент позволяет создавать динамические чертежи. Динамические чертежи, созданные в GeoGebra позволяют на одном уроке решить больше задач, рассмотреть все случаи решения той или иной задачи, доказательство теоремы, рассмотреть частные случаи и т. д [1].
Геометрическая интерпретация решения уравнения p(p-3)x+p=0.
1. При p=3 графики функций y=p(p-3)x и y=-p параллельны, точек пересечения нет (рис. 1).
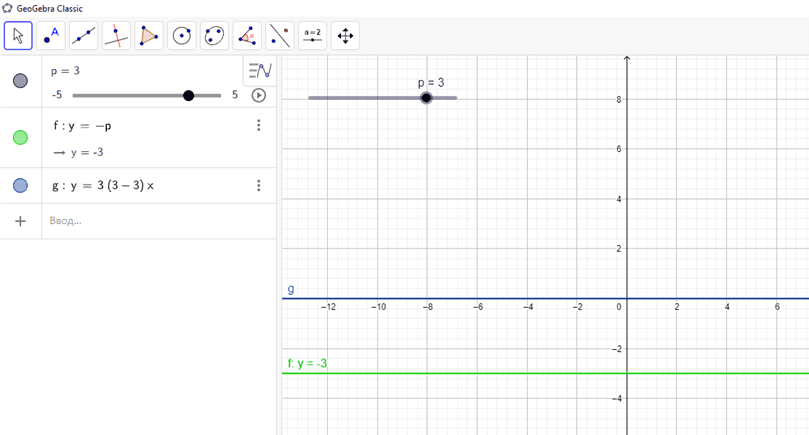
Рис. 1. Первый случай
2. При p≠3 и p≠0 графики функций y=p(p-3)x и y=-p пересекаются в одной точке. Абсцисса точки пересечения является корнем уравнения (рис. 2).
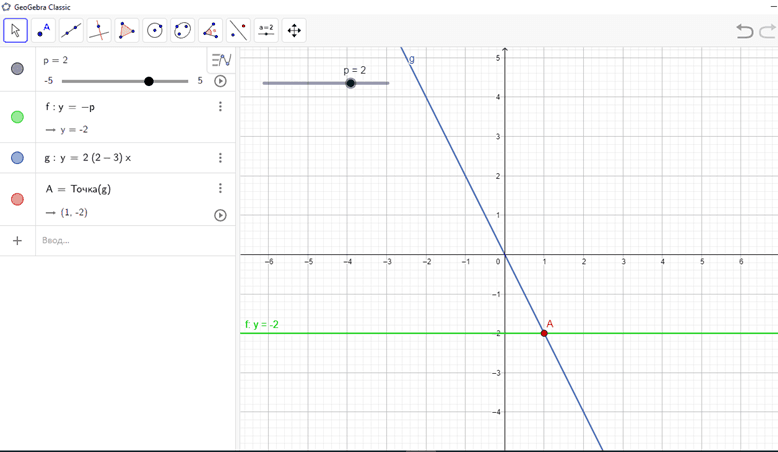
Рис. 2. Второй случай
3. Уравнение корней не имеет. При p=0 графики функций y=p(p-3)x и y=-p совпадают, все точки общие. Уравнение имеет бесконечное число корней (рис. 3).
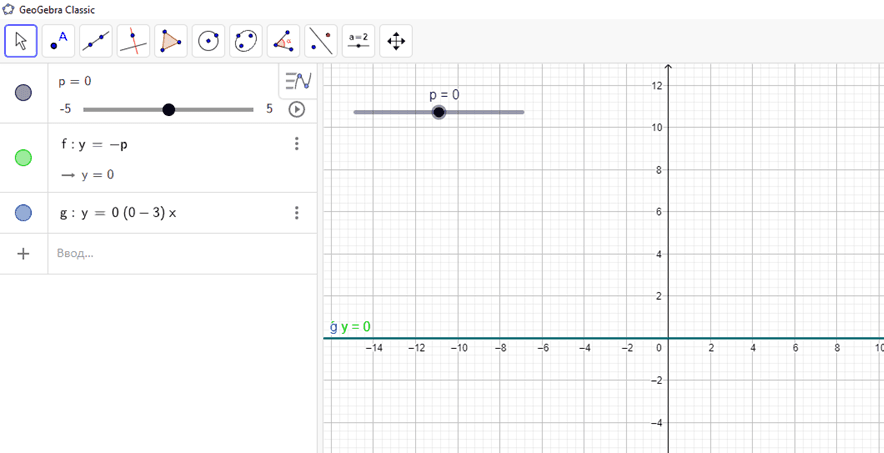
Рис. 3. Третий случай
Применяя информационные технологии в обучении математики ребята выступают в роли исследователей, которые вооружены простыми средствами, позволяющими им провести анализ, наблюдение, эксперимент и зафиксировать показания изучаемого объекта и процесса исследования [2, c. 90].
Учебно-методический комплекс Мордковича А.Г. рассматривает возможности систематического внедрения в курс алгебры 7-9 классов задач с параметрами [3].
Наглядные представления решения заданий с параметрами расширяют возможности обучающихся по конструированию новых заданий, на смену репродуктивных заданий на знание, понимание и применение приходят экспериментальные лабораторные работы, в которых ребята проводят анализ, синтез и тем самым повышают уровень обученности детей.

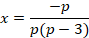
.png&w=640&q=75)