Начиная с первого класса ребенок сталкивается с решением простых текстовых математических задач. Простая текстовая задача решается в одно действие. На первоначальных этапах решения задач обучающиеся используют вещественные модели, которые помогают ребенку наглядно продемонстрировать возможности сложения или вычитания в реальной жизненной ситуации. Например, «Было пять яблок, одно съели. Сколько осталось яблок?». Используя наглядные средства осуществить понимание задачи. При решении таких задач необходимо перевести задачу на математический язык и составить математическую модель. При решении данной задачи составляется числовое выражение «5 – 1», решением полученной модели получаем «4», после этого необходимо вернуться к задаче и составить ответ. Ответ: 4 яблока осталось на столе.
Таксономия Б. Блума наиболее полно отражает уровни усвоения учебного материала. Каждому уровню усвоения учебного материала соответствуют свои вопросы [1, 3]. Учитель, тонко разбираясь в вопросах разных типов, может управлять процессом познания на каждом из уровней, выстраивать обучение так, чтобы новые знания проходили последовательно через уровни понимания, использования, анализа, синтеза, позволяли бы ребенку становиться личностью через выработку его жизненной (субъектной) позиции. В таблице 1 представлена сущность каждой категории целей [2, c. 123].
Таблица 1
Категории целей
|
Категории целей |
Деятельность ученика |
|---|---|
|
Знание |
запоминание и воспроизведение изученного материала от конкретных фактов до целостной теории |
|
Понимание |
преобразование материала из одной формы выражения в другую, интерпретация материала, предположение о дальнейшем ходе явлений, событий |
|
Применение |
возможность использовать изученный материал в конкретных условиях и новых ситуациях |
|
Анализ |
умение разбить материал на составляющие так, чтобы ясно выступала структура |
|
Синтез |
умение комбинировать элементы, чтобы получить целое, обладающее новизной |
|
Оценка |
умение оценивать значение того или иного материала |
По таксономии Блума представим уровни (этапы) усвоения решения текстовой задачи (табл. 2).
Таблица 2
Работа над текстовой задачей по таксономии Блума
|
Уровни |
Этапы |
Возможные модели |
|---|---|---|
|
Знание |
Идентификация |
Условие и вопрос. |
|
Понимание
|
Визуализация текстовой задачи |
Наглядные средства (палочки, кружочки) Схематический чертеж Краткая запись |
|
Применение |
Моделирование |
Выражение, равенство, уравнение |
|
Анализ и синтез |
Проектирование |
Новые задачи на основе данной |
|
Оценка |
Оценка |
Решение задачи |
Рассмотрим задачу и представим этапы работы над задачей в соответствии с таксономией Блума.
Задача 1. Наташа вымыла 5 тарелок, а Юля вымыла 4 тарелки. Сколько всего тарелок вымыли дети?
На первом этапе при решении текстовых задач обучающиеся погружаются в задачу и учатся выявлять условие и вопрос задачи и определять тип задачи.
Условие: Наташа вымыла 5 тарелок, а Юля вымыла 4 тарелки.
Вопрос: Сколько всего тарелок вымыли дети?
Задача простая, решается в одно действие.
На втором этапе обучающиеся для лучшего понимания учатся визуализировать текстовую задачу. На рисунке 1 представлена модель в виде краткой записи, а на рисунке 2 – схематический чертеж.
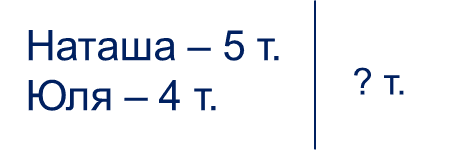
Рис. 1. Краткая запись
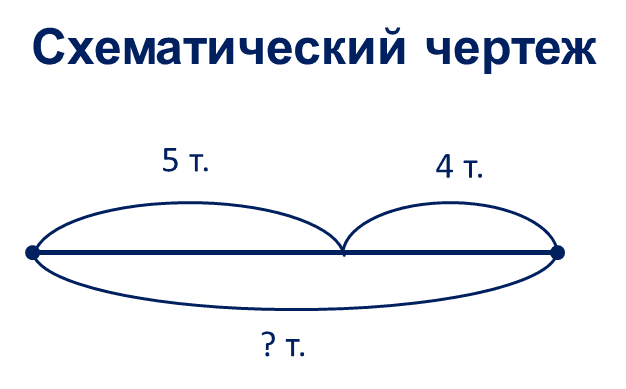
Рис. 2. Схематический чертеж
Третий этап является самым важным, ребята учатся применять полученные знания в решении задач. На данном этапе с помощью метода моделирования учатся оформлять решение задачи. В нашей задаче моделью является числовое выражение «5 + 4», решением полученной модели получаем «9», после этого необходимо вернуться к задаче и составить ответ.
Решение: 5 + 4 = 9 (т.)
Ответ: 9 тарелок вымыли дети.
На этапе «Анализ и синтез» обучающиеся учатся по данной задаче проектировать новые задачи (противоположные, обратно-противоположные и др.).
Задача 2. У девочек было 9 тарелок. Наташа вымыла 5 тарелок. Сколько тарелок вымыла Юля?
Задача 3. У девочек было 9 тарелок. Юля вымыла 4 тарелки. Сколько тарелок вымыла Наташа?
Задача 4. Наташа вымыла 5 тарелок, а Юля вымыла 4 тарелки. На сколько больше тарелок вымыла Наташа?
Задача 5. Наташа вымыла 5 тарелок, а Юля вымыла 4 тарелки. На сколько меньше тарелок вымыла Юля?
На заключительном этапе обучающиеся учатся оценивать себя и других участников образовательного процесса.
Оцените решение задачи вашего сверстника Иванова Николая по следующим критериям.
5 баллов – решение и оформление задачи составлено верно.
4 балла – верно составлена краткая запись или схематический чертеж к задаче, правильно оформлено решение, но ответ задачи указан без пояснения.
3 балла – верно составлена краткая запись или схематический чертеж к задаче, но решение задачи неверно.
2 балла – решение задачи представлено неверно.
Задача 1. Наташа вымыла 5 тарелок, а Юля вымыла 4 тарелки. Сколько всего тарелок вымыли дети?
Решение: 5 + 4 = 10 (т.)
Ответ: 10.
При осуществлении оценки решения данной задачи обучающийся должен сам оформить решение задачи. Оценить сверстника по установленным критериям.
На простой текстовой задаче рассмотрели возможности применения Таксономии Блума. Данная таксономия поможет выявить уровни (этапы) усвоения по решению текстовой задачи в начальной школе.
Данные этапы работы с текстовой задачей помогут учителям выстроить процесс обучения таким образом, что у детей будет полное представление и понимание.

.png&w=640&q=75)