Важнейшими характеристиками надежности технических объектов являются ресурс и остаточный ресурс. Эти величины не могут считаться детерминированными, так как для разных, однородных по характеристикам технических объектов эти величины принимают различные значения [1-4]. Знание вида закона распределения позволяет сделать с некоторой вероятностью прогноз о величинах ресурса и остаточного ресурса. В работе [4] предложен один из вероятностных методов оценки ресурса и остаточного ресурса. Этот метод основан на статистических данных, которые свидетельствуют о том, что диапазон изменения коэффициента вариации для технических объектов является достаточно узким (0,2 – 0,4). Цель исследования заключается в сравнении оценок ресурса и остаточного ресурса при различных предположениях о законе их распределения и создании программ в системе Mathcad, реализующих алгоритм расчета.
В расчетах используются коэффициент вариации ρ, выборочное среднее квадратическое отклонение σ и выборочная средняя 
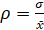 , (1)
, (1)
Следует отметить, продление ресурса экономически целесообразно, если в допустимых пределах увеличиваются затраты на эксплуатацию объекта. В этом отношении целесообразно сформулировать и решить задачу определения оптимального ресурса [3, 4].
Введем обозначения: θ – ресурс объекта, принимается, что он является случайной величиной; 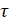 – время. В теории надежности вводится функция
– время. В теории надежности вводится функция  , которая называется функцией выживаемости. Статистическое содержание этой функции состоит в том, что она показывает, сколько в среднем объектов из большой совокупности доживают, как минимум, до времени τ
, которая называется функцией выживаемости. Статистическое содержание этой функции состоит в том, что она показывает, сколько в среднем объектов из большой совокупности доживают, как минимум, до времени τ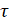 . Функция выживаемости связана с интегральной функцией
. Функция выживаемости связана с интегральной функцией 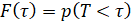 равенством
равенством
 . (2)
. (2)
Плотность вероятности ресурса является производной от интегральной функции
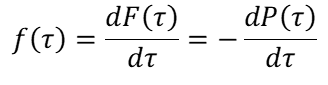 (3)
(3)
Если отсчет времени ведется от момента 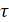 , до которого объект уже эксплуатировался, то
, до которого объект уже эксплуатировался, то 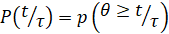 – условная вероятность того, что остаточный ресурс будет не меньше величины t при условии, что объект функционировал от 0 до момента времени
– условная вероятность того, что остаточный ресурс будет не меньше величины t при условии, что объект функционировал от 0 до момента времени 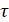 .
.
Для оценки функции выживаемости в данной работе рассмотрены логарифмически нормальное, нормальное, усеченное нормальное и показательное распределения.
Введем относительную случайную величину
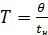 , (4)
, (4)
где tн – нормативный ресурс технического объекта, θ – ресурс.
В ряде работ [2-4] рассмотрена вероятностная модель определения ресурса технического объекта на основе логарифмически нормального закона распределения. Такой закон распределения часто применяется для описания дефектов, возникающих по причине физического износа, когда независимые случайные факторы определяют результирующий фактор по закону произведения. Плотность вероятности для логарифмически нормальной случайной величины имеет вид
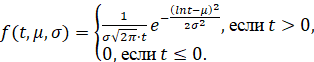 (5)
(5)
Здесь -∞<μ<+∞, σ>0 – параметры распределения, при  , a>0.
, a>0.
Для оценки ресурса необходимо установить связь параметров μ и σ с числовыми характеристиками случайной величины. Математическое ожидание определяется по формуле:
 . (6)
. (6)
Дисперсия равна
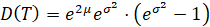 . (7)
. (7)
Связь коэффициента вариации с параметром σ определяется формулой:
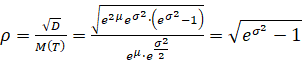 ,
, 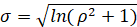 . (8)
. (8)
В системе Mathcad [5] составлена программа для реализации алгоритма определения параметров. В этой программе определяется функция Лапласа
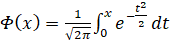 , (9)
, (9)
формулируется уравнение
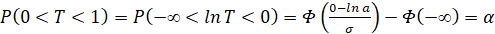 ,
,  . (10)
. (10)
Для приближенного решения уравнения
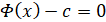 (11)
(11)
используется встроенная функция root( ) в алгоритме программы на рис. 1.

Рис. 1. Функциональная схема программы в системе Mathcad
На рис. 2 представлены зависимости среднего ресурса (TSi) от коэффициента вариации (ρi) при различных значениях вероятности α.
 Рис. 2. Зависимость среднего ресурса от коэффициента вариации при различных α
Рис. 2. Зависимость среднего ресурса от коэффициента вариации при различных α
Представляет интерес зависимость среднего ресурса от вероятности α при различных значениях коэффициента вариации. Зависимости такого вида представлены на рис. 3.
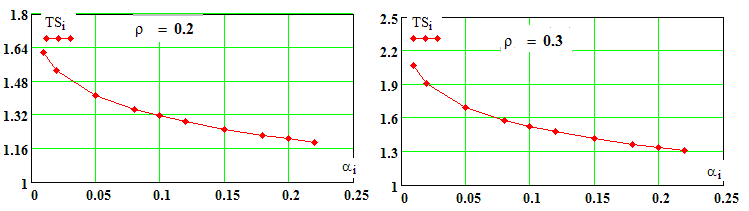 Рис. 3. Зависимость среднего ресурса от α при различных значениях коэффициента вариации
Рис. 3. Зависимость среднего ресурса от α при различных значениях коэффициента вариации
При заданных значениях вероятности α увеличение коэффициента вариации ресурса приводит к увеличению среднего ресурса (рис. 2). При увеличении α (то есть при увеличении погрешности прогноза) происходит уменьшение среднего ресурса при любом значении коэффициента вариации.
Для получения оценки остаточного ресурса следует рассмотреть условное распределение логарифмически нормальной случайной величины.
Рассмотрим распределение ресурса при условии, что объект уже проработал некоторое время tk, тогда 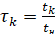 – относительный возраст объекта и остаточный ресурс
– относительный возраст объекта и остаточный ресурс
 .
.
Введем следующие события
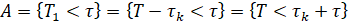 ,
,  ,
,
тогда
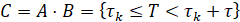 .
.
Вероятность произведения событий найдем по формуле:
 (12)
(12)
Отсюда получаем формулу:
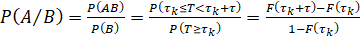 . (13)
. (13)
Таким образом, интегральная функция распределения случайной величины 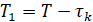 имеет вид
имеет вид
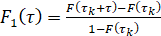 (14)
(14)
Плотность вероятности определяется по формуле:
 . (15)
. (15)
Кривая вероятностей условного распределения, графики интегральной функции и функции выживаемости изображены на рис. 4.
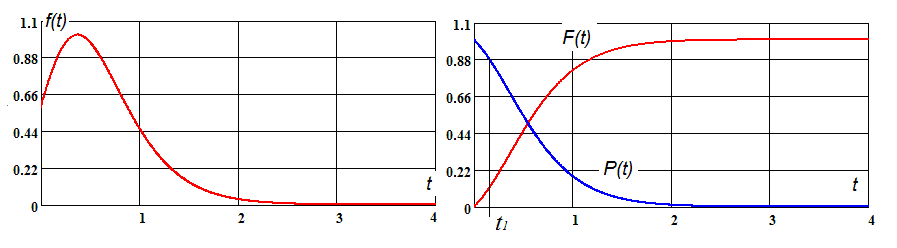 Рис. 4. Кривая вероятностей условного распределения, графики интегральной функции и функции выживаемости условного распределения
Рис. 4. Кривая вероятностей условного распределения, графики интегральной функции и функции выживаемости условного распределения
Функция выживаемости позволяет определять величину остаточного ресурса с некоторой вероятностью по формуле
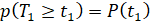 . (16)
. (16)
Рассмотрим методы оценки ресурса и остаточного ресурса при выборе различных законов распределения случайных величин.
Предполагается, что случайная величина 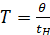 имеет показательное распределение с параметром λ>0. Это означает, что интегральная функция имеет вид
имеет показательное распределение с параметром λ>0. Это означает, что интегральная функция имеет вид
 (17)
(17)
Для показательного распределения справедливо равенство
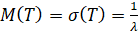 .
.
Коэффициент вариации определяется формулой
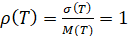 . (18)
. (18)
Из условия
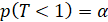 ,
,
где α=0,05-0,1, можно найти параметр распределения, то есть величину λ.
Условие T<1 означает, что 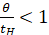 , или θ<tН, то есть ресурс окажется меньше нормативного. Находим параметр показательного распределения
, или θ<tН, то есть ресурс окажется меньше нормативного. Находим параметр показательного распределения
 .
.
Таким образом, 1-e-λ=α, тогда e-λ=1-α, следовательно,
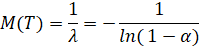
Функция выживаемости случайной величины определяется формулой
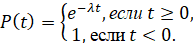
Следует заметить, применение показательного распределения для оценки остаточного ресурса технического объекта не является обоснованным. Остаточный ресурс должен зависеть от наработки в силу износа составляющих технического объекта, деградации свойств материала. Это означает, что закон распределения и его параметры не могут оставаться неизменными, что противоречит свойству показательного распределения.
Если ресурс T имеет нормальный закон распределения, то дифференциальная функция имеет вид
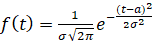 .
.
Пусть p(T<1)=α, тогда
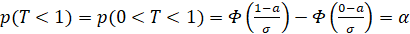 .
.
Здесь неизвестны два параметра, поэтому необходимо дополнительное условие. Если, например, известен коэффициент вариации
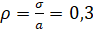 ,
,
то σ=0,3a и тогда получаем уравнение
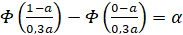 ,
, 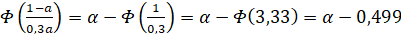 .
.
При значении α=0,1 получаем уравнение  . Решение этого уравнения в системе Mathcad находится с помощью функции root(…) [5].
. Решение этого уравнения в системе Mathcad находится с помощью функции root(…) [5].
Для прогноза остаточного ресурса используется формула для интегральной функции условного распределения


Ресурс и остаточный ресурс не могут быть отрицательными. По этой причине необходимо рассмотреть усеченное нормальное распределение.
Дифференциальная функция определяется следующим образом
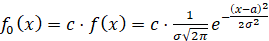 ,
,
где c – постоянная, которая находится из условия
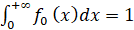 .
.
В результате вычисления интеграла получаем формулу
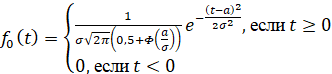 (19)
(19)
Следует заметить, что в общем случае математическое ожидание, дисперсия и среднее квадратическое отклонение связаны с параметрами распределения сложными зависимостями. Однако, при условии М(T)>3σ можно применять более простые формулы M(T)≈a, σ(T)≈σ, следовательно, 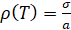 . Параметры распределения находим из системы уравнений
. Параметры распределения находим из системы уравнений
 ,
, 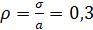 ,
,
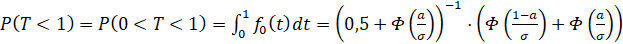 .
.
Таким образом, 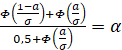 и σ=0,3a.
и σ=0,3a.
Сформулируем следующую задачу: газоперекачивающий агрегат имеет нормативный ресурс 20 лет, он проработал 15 лет. Необходимо найти вероятность того, что остаточный ресурс будет не меньше 10 лет.
Таким образом, в относительных единицах имеем:
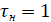 ,
, 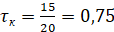 ,
, 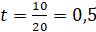 .
.
Параметры распределений определяются из условий
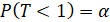 ,
,  ,
,  , (кроме показательного распределения).
, (кроме показательного распределения).
На рис. 5 показан фрагмент вычислений в Mathcad значения функции выживаемости для логарифмически нормального распределения.

Рис. 5. Определение интегральной функции и функции выживаемости условного распределения для логарифмически нормального распределения
Таким образом, P(T0>0,5)=0,734.
Графики функции выживаемости и интегральной функции в масштабе, удобном для графического определения значений, представлены на рис. 6.
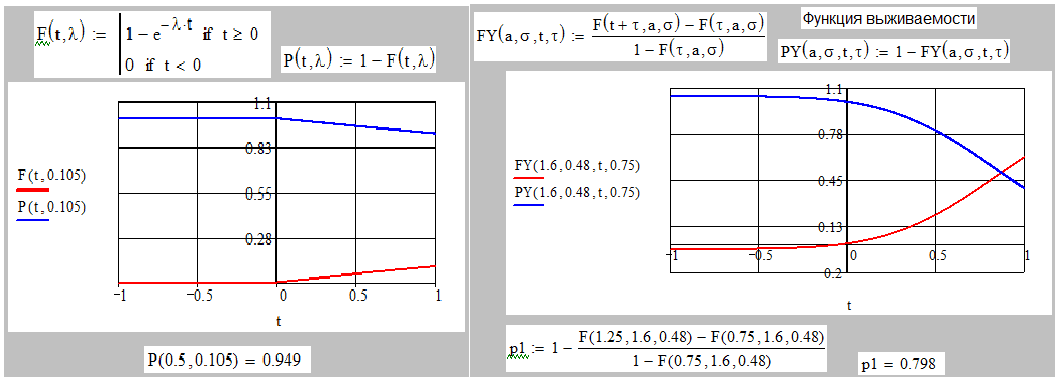
Рис. 6. Графики интегральной функции и функции выживаемости показательного и нормального распределений
Таким образом, P(T0>0,5)=0,949.
Графики функции выживаемости и интегральной функции для нормального распределения представлены на рис. 7. Результат вычисления:
P(T0>0,5)=0,798
Вычисления при условии M(T)>3⋅σ представлены на рис. 7.

Рис. 7. Вычисление условной вероятности, графики интегральной функции и функции выживаемости усеченного нормального распределения
Общие результаты вычислений приведены в таблице.
Таблица
Результаты вычислений
|
Закон распределения |
α |
ρ |
Параметры распределения |
Наработка агрегата |
P(T0>0,5) |
|---|---|---|---|---|---|
|
Показательное |
0,1 |
1 |
λ=0,105 |
|
0,948 |
|
Нормальное |
0,1 |
0,3 |
a=1,6, σ=0,48 |
|
0,798 |
|
Усеченное нормальное |
0,1 |
0,3 |
a=1,6, σ=0,48 |
|
0,798 |
|
Логарифмически нормальное |
0,1 |
0,3 |
a=1,457, σ=0,294 |
|
0,734 |
Заключение
- При вероятностной оценке остаточного ресурса можно рекомендовать нормальное и логнормальное распределения. Результаты отличаются несущественно.
- Предложены программы в системе Mathcad, которые позволяют находить параметры заданного закона распределения и проводить анализ при различных сочетаниях факторов.
- Для получения более достоверной информации целесообразно формировать базу статистических данных для конкретных технических объектов.



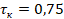

.png&w=640&q=75)