Модель диагностики состояния подшипников ротора по вибрациям

Введение. Вопросам математического моделирования поперечных и осевых колебаний вала насоса при импульсных нагрузках посвящены работы ряда авторов [1-3, 6, 7]. В работах [1, 6] рассматриваются стержневые модели для изучения продольных колебаний. Модели исследования поперечных колебаний приведены в работах [2, 3, 7]. Решения начально-краевых задач осуществляется методом Фурье и методом конечных разностей. Представляет интерес влияние на параметры колебаний способа креплений балки. При работе подшипников неисправности могут приводить к уменьшению жесткости, что можно моделировать изменением способа крепления балки.

Цель исследования заключается в создание алгоритма и программы для моделирования процесса износа или повреждений подшипников центробежного насоса. Перечислим основные задачи исследования.

1. Сформулировать и решить начально-краевую задачу поперечных колебаний балки при импульсных нагрузках;
2. Разработать программу в системе Mathcad [4], в которой реализовать метод Фурье решения начально-краевой задачи с уравнениями поперечных колебаний балки для различных краевых условий;
3. Провести анализ способа креплений балки на поперечные перемещения сечений, скоростей и ускорений.

Рассмотрим конкретный пример насоса, конструктивная схема которого представлена на рис. 1.

Рис. 1. Конструктивная схема насоса типа 12НДс-Нм-т-Е
1 – вал; 2 – корпус; 3 – крышка корпуса; 4 и 5 – втулки вала; 6 – рабочее колесо; 7 – кольцо уплотняющее; 8 – узел уплотнения вала; 9 – подшипник скольжения; 10 – радиально упорный подшипник

Данный насос – это центробежный насос двустороннего входа, предназначен для перекачивания незагрязненных механическими примесями нефтепродуктов. Расчетная схема вала насоса представляет собой балку с постоянным круглым поперечным сечением (рис. 2). Она нагружается начальным импульсом или определением начального перемещения, которое в основном происходит из-за дисбаланса ротора.

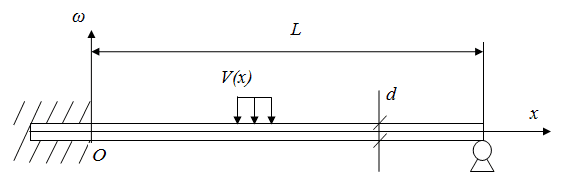
Рис. 2. Расчетная схема вала насоса

Поперечные колебания балки определяются уравнением четвертого порядка в частных производных:

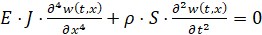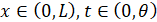,,    (1)

где w(t,x) – отклонение сечения x балки от положения равновесия в момент времени t, E – модуль упругости, J – момент инерции балки круглого сечения (вала) 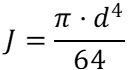, ρ – плотность материала, S – площадь поперечного сечения .

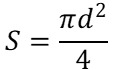Рассмотрим краевые условия при креплении «шарнир – жёсткая заделка».

Краевые условия при шарнирном креплении характеризуют отсутствие поперечных перемещений и допускают возможность поворота в плоскости w0x. Они имеют вид:

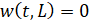,    (2)

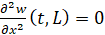.    (3)

При жёсткой заделке физический смысл условий заключается в том, что отсутствуют перемещения и невозможны вращения в плоскости w0x:

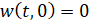,    (4)

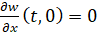.    (5)

Начальные условия принимаются в виде:

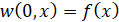,    (6)

.    (7)

Условия (6) и (7) определяют характер нагрузки на балке. Функция f(x) задает начальное распределение поперечных перемещений сечений балки по длине, функция F(x) задает распределение поперечной скорости сечений балки. Введем обозначение:

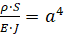.    (8)

При подстановке (8) в уравнение (1) получим:

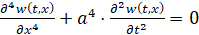.    (9)

Решение задачи можно найти методом разделения переменных. Решение необходимо искать в виде произведения двух функций, одна из которых U(x) зависит только от х, другая T(t) зависит только от t, тогда:

.    (10)

После подстановки w(t,x) в уравнение (9) получим:

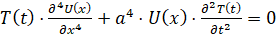.    (11)

Из (11) переходим к равенству:

.    (12)

Равенство двух функций с различными независимыми переменными возможно, если они принимают постоянные значения. Получаем два обыкновенных дифференциальных уравнения второго и четвертого порядков с постоянными коэффициентами:

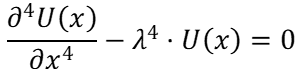,    (13)

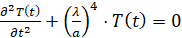.    (14)

Далее рассмотрим краевую задачу:

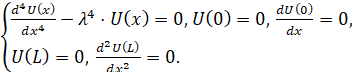    (15)

Найдем общее решение (15), составив характеристическое уравнение:

.    (16)

Полученное уравнение имеет четыре корня:

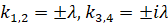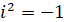,      (17)

В качестве независимых решений удобно взять функции

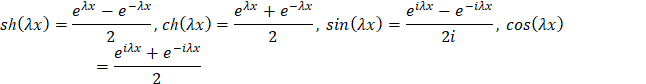. (18)

Общее решение уравнения (15) запишем в виде:

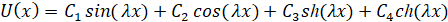.    (19)

Постоянные C₁,C₂,C₃,C₄ будем находить из краевых условий (2)-(5).

    (20)

Из первых двух уравнений следует, что C₂=-C₄, C₁=-C_3, тогда:

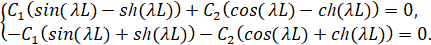     (21)

Условие неопределенности системы (21):

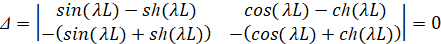.    (22)

После вычислений определителя получаем уравнение относительно λ:

.    (23)

Уравнение (23) имеет приближенное решение, когда th(x)=0, th(λ)≈1:

.

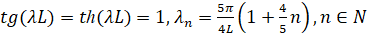Предположим, что C₁=1, тогда находим C₂:

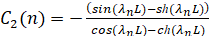.    (24)

Собственные функции краевой задачи:

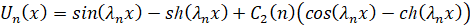.     (25)

Находим решение уравнения:

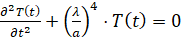.    (26)

Характеристическое уравнение и его корни:

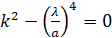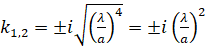,      .    (27)

Общее решение дифференциального уравнения имеет вид:

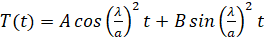    (28)

Решение начально-краевой задачи должно удовлетворять также начальным условиям. Для достижения такой цели составим ряд:

.    (29)

Из начального условия (6) следует:

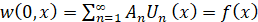.    (30)

Умножая обе части тождества (30) на U_n(x) и интегрируя в пределах от 0 до L, получим равенство:

.    (31)

Из полученного равенства следует формула для вычисления коэффициента A_n:

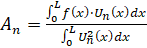.    (32)

Используя начальное условие (7), аналогично получим формулу для вычисления коэффициента B_n

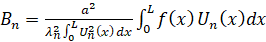.    (33)

Таким образом, получим решение начально-краевой задачи в виде ряда:

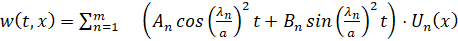.    (34)

Рассмотрим результаты расчетов в системе Mathcad. В таблице представлены исходные данные для расчета.

Таблица

Исходные данные

Начальное распределение скорости и перемещений сечений вала по его длине показано на рис. 3. Распределение скорости поперечных сечений балки имитирует внешний поперечный удар.

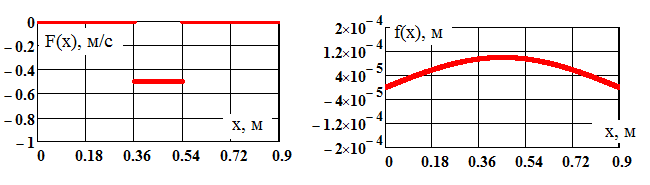
Рис. 3. Начальное распределение скорости и перемещений поперечных сечений вала

Построив графики поперечных перемещений разных сечений вала в зависимости от времени для конечного числа слагаемых ряда Фурье, мы можем увидеть, как меняется спектр поперечных перемещений.

Рис. 4. Перемещения и скорость среднего сечения вала при наличии только начальной скорости: 1) 10 слагаемых ряда, 2) только первый член ряда, 3) первых 3 члена ряда

Виброскорость и виброускорение определяются как производные первого и второго порядков по времени от ряда Фурье.

Форма прогиба балки и распределение скорости в заданный момент времени показаны на рис. 5.

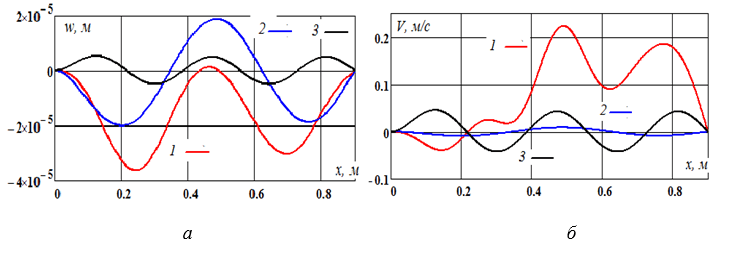
Рис. 5. Суммарный прогиб и скорость сечений вала при t=0,015 с
1) 10 слагаемых; 2) только третий член ряда; 3) только пятый член ряда

Используя результаты [7], сравним показатели поперечных перемещений вала, виброскорости и виброускорения в одинаковых условиях, при жестком креплении концов вала (подшипники полностью в исправном состоянии, нет никаких люфтов) и при шарнирном закреплении концов вала (оба подшипника неисправны и на обоих концах вала присутствует некоторый люфт) с рассмотренным выше случаем.

На рис. 6 приведены расчетные схема для этих случаев.

Рис. 6. Расчетные схемы вала при жестком и шарнирном креплении

Сравнение поперечных перемещений сечения центра вала в зависимости от времени для десяти слагаемых ряда Фурье приведено на рис. 7,а.

Здесь мы можем наблюдать, что максимальное отклонение вала от состояния равновесия происходит, когда оба подшипника имеют неисправности, в случаях же, когда один подшипник неисправен, или оба подшипника исправны, наблюдаем почти одинаковую амплитуду отклонений.

Рис. 7. Перемещения центра вала (а), скорость центра (б) при наличии только начальной скорости, для различных видов креплений: 1) оба подшипника в порядке; 2) оба подшипника неисправны; 3) один подшипник неисправен, другой в порядке

С виброскоростью (рис. 7,б) и виброускорением (рис. 8,а) сечения центра вала мы можем наблюдать другую ситуацию. Максимальные значения виброскорости сечения центра вала принимает также тогда, когда оба подшипника в порядке.

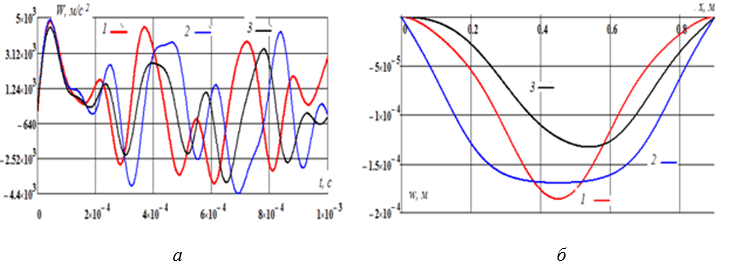
Рис. 8. а) Зависимость виброускорения сечения центра вала от времени для различных видов креплений: 1) оба подшипника в порядке; 2) оба подшипника неисправны; 3) один подшипник неисправен, другой в порядке; б) Распределение прогиба сечений вала по длине для различных видов креплений в момент времени t=0,001

При выходе из строя одного подшипника, максимальное значение прогиба смещается в сторону этого подшипника, а при выходе из строя обоих подшипников, максимальный прогиб расположен посередине.

Заключение

1. Показана зависимость параметров поперечных колебаний балки от вида опор. Изменение параметров можно трактовать как результат изменения состояния подшипников вала центробежного насоса.
2. Разработана программа в системе Mathcad, позволяющая провести сравнение перемещения, скорости и ускорения при поперечных колебаниях вала при трех видах крепления вала: «шарнир», «жесткая заделка», «шарнир-жесткая заделка».
3. Показано, что при регистрации параметров вибрации в местах близких к подшипникам наблюдается существенная зависимость параметров колебаний от вида опоры, то есть состояния подшипника.

1. Араманович И. Г., Левин В.И. Уравнения математической физики: учеб. пособие. – Москва: Наука, 1969. 288с.
2. Доев В. С. Поперечные колебания балок: учебное пособие. М.: КНОРУС, 2016. 412 с.
3. Никитина Т. Ю. Динамика поперечных колебаний вертикально защемленной балки // Вестник государственного университета морского и речного флота имени адмирала С.О. Макарова. № 3(22). 2013. С.79-88.
4. Охорзин В. А. Прикладная математика в системе MATHCAD: учеб. пособие. 2-е изд., исп. и доп. Санкт-Петербург: Издательство «Лань», 2008. 352 с.
5. Слиденко А.М., Слиденко В.М. Исследование дискретно-непрерывной адаптивной модели ударного устройства // Математическое моделирование. Т.27, №1, 2015. С.54-64.
6. Слиденко А.М. Исследование поперечных колебаний балки численно-аналитическими методами. Научно-технический журнал: Насосы. Турбины. Системы. 2 (39). 2021. С. 47-55.