Для разработки систем диагностики трубопроводного транспорта высоковязкой жидкости нужно иметь представление о параметрах жидкости при отсутствии дефектов и при их наличии. Получению такой информации способствует математическое моделирование, в котором формулируются начально-краевые задачи с использованием уравнений теплопроводности и движения жидкости [1-5, 8]. Для решения таких задач можно использовать численные методы и специализированные программы, например, Mathcad [6]. Разработка методов комплексной технической диагностики и профилактического сервиса технологического оборудования нефтетранспортных трубопроводных систем в настоящее время является актуальной [5].
Объектом исследования является установка усреднения параметров жидкости с большой вязкостью АО «Воронежсинтезкаучук». Принцип работы установки заключается в том, что жидкости с разными физическими характеристиками поступают в емкость, где происходит их смешение с помощью мешалки и циркуляция насосом для получения жидкости с установленными параметрами. Насосы обеспечивают бесперебойную подачу высоковязкого вещества по трубопроводу для дальнейших операций по получению продукции. С внешней стороны трубопровода осуществляется подогрев жидкости.
Цель исследования заключается в разработке алгоритма и компьютерной программы для оценки параметров теплообмена на участке трубопроводного транспорта высоковязкой жидкости и моделировании процессов нарушения режима внешнего обогрева трубопровода.
В процессе исследования решаются следующие задачи.
- Постановка начально-краевой задачи с заданным распределением температуры на входе трубопровода при известном распределении скорости потока в поперечном сечении;
- Определение вида и параметров разностной схемы для решения начально-краевой задачи;
- Выбор и определение основных параметров модельной задачи с известным аналитическим решением;
- Реализация алгоритма в системе Mathcad, проведение вычислений.
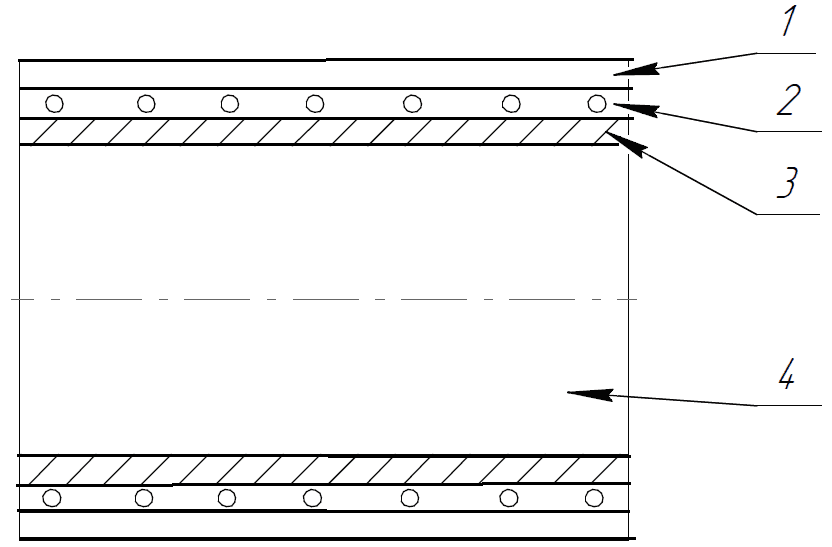
Основные геометрические параметры участка трубопровода с внешним подогревом представлены на рис. 1.
При нарушении теплоизоляции через стенку трубопровода происходит теплообмен с окружающей средой, в результате чего температура термоэластопласта (жидкости с большой вязкостью) понижается.
а
б
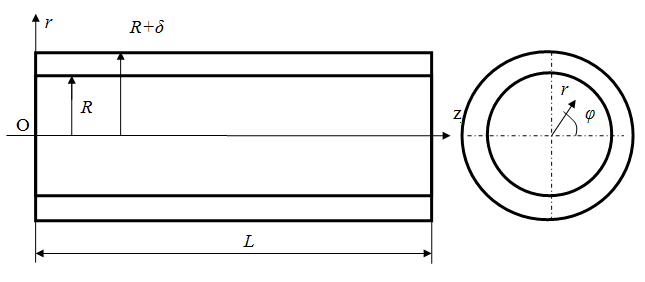
Рис. 1. а) Разрез исследуемого участка трубопровода с подогревом: 1 – теплоизоляция, 2 – подогревательный элемент, 3 - стенка трубопровода, 4 – жидкость (термоэластопласт); б) Основные геометрические параметры исследуемого участка трубопровода
В нормальном режиме обеспечивается подогрев трубопровода со стороны внешней стенки, при этом температура на внешней стороне стенки при нормальной работе системы подогрева предполагается постоянной. Из экспериментальных данных известен профиль скорости жидкости, которая зависит только от радиальной координаты трубопровода [8]. Таким образом, предполагается, что по длине трубопровода скорость не меняется.
Начально-краевую задачу составляет уравнение теплопроводности для жидкости (1), уравнение теплопроводности для стенки трубопровода (2), уравнение, определяющее распределение скорости по сечению (3), уравнение неразрывности (4):
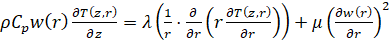 ,
, 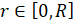 , (1)
, (1)
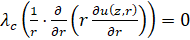 ,
, 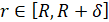 ,
, 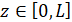 , (2)
, (2)
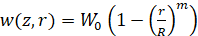 , (3)
, (3)
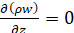 ,
, 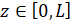 ,
, 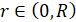 . (4)
. (4)
В приведенных уравнениях приняты следующие обозначения:
w(z,r) – скорость термоэластопласта в сечении z, м/с;
T(z,r) – температура термоэластопласта в сечении z, К; – плотность термоэластопласта, кг/м3;
λ – коэффициент теплопроводности термоэластопласта, Вт/(м К);
λc – коэффициент теплопроводности стальной стенки, Вт/ (м К);
Cp – теплоемкость термоэластопласта, Дж/(кг К); – температура термоэластопласта на входе в трубопровод; – температура на внешней стороне стенки трубопровода.
График распределения скорости по сечению и распределение температуры в начальном сечении представлены на рис. 2.
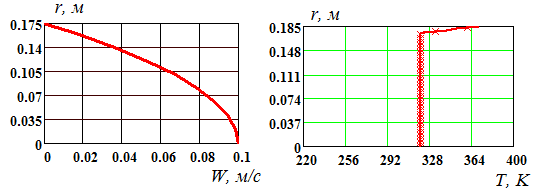
Рис. 2. Распределения скорости и температуры термоэластопласта в начальном сечении; Исходные данные: ν=1,4-1,55⋅10-4м2/с; Сp=1380-1400 Дж/(кг К); λ=0,11Вт/м⋅К; λс=15Вт/м⋅К; ρ=1000-1015 кг/м3
Приближенное решение задачи (1)-(4) находится методом конечных разностей в комбинации с аналитическим решением для стенки трубопровода [4, 7]. Основные параметры сеточной области:
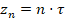 ,
, 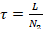 ,
, 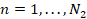 ,
, 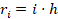 ,
, 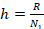 ,
, 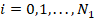 .
.
Приняты следующие обозначения сеточных функций:
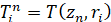 ,
, 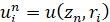 ,
, 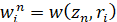 .
.
Разностная схема (5) вместе с уравнением (6) и краевыми условиями (7), (8) на каждом слое по длине трубопровода представляет собой систему линейных уравнений, которая решается методом прогонки. Принята двухслойная разностная схема с весами, параметр σ определяет тип разностной схемы:
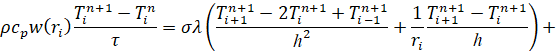
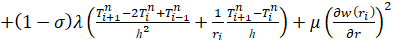 ,
, 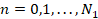 ,
, 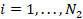 , (5)
, (5)
Аналитическое решение уравнения (2) в каждом поперечном сечении трубопровода
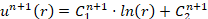 ,
, 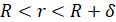 . (6)
. (6)
Аппроксимация условий сопряжения жидкой области со стенкой имеет вид:
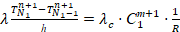 . (7)
. (7)
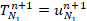 ,
, 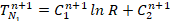 . (8)
. (8)
Условие симметрии решения:
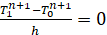 . (9)
. (9)
Условие на внешней границе трубопровода:
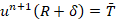 ,
, 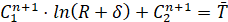 . (10)
. (10)
Аппроксимация начальных условий:
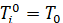 ,
, 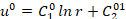 . (11)
. (11)
Преобразуя систему уравнений к стандартному виду, получаем систему уравнений (12)
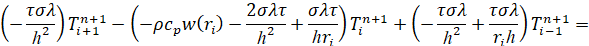
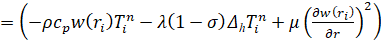 . (12)
. (12)
Введем обозначения коэффициентов системы
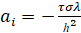 ,
, 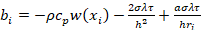 ,
, 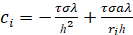 ,
,
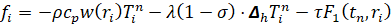 .
.
С учетом принятых обозначений система уравнений имеет вид:
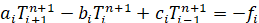 . (13)
. (13)
Системы (14) на каждом слое по длине решается методом прогонки, с учетом краевых условий. Для решения задачи используется общая функциональная схема программы (рис. 4).
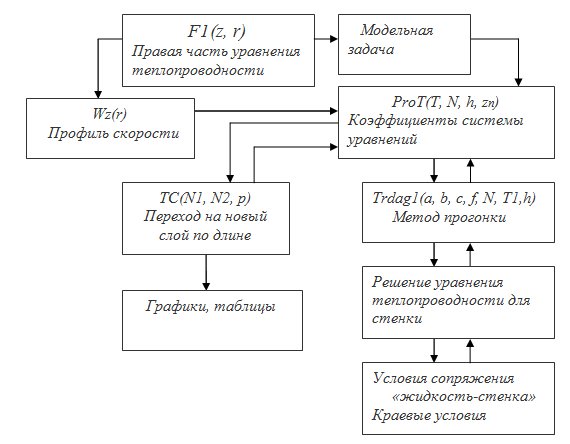
Рис. 4. Общая функциональная схема программы
Профиль температуры в различных сечениях трубопровода показан на рис. 5,а. У стенки температура жидкости очень быстро принимает значение температуры стенки (с внутренней стороны). Температуры внешней и внутренней стенки трубопровода мало отличаются, что является следствием большого значения коэффициента теплопроводности. Малое значение коэффициента теплопроводности жидкости при малой скорости движения жидкости приводит к большому температурному градиенту в поперечном сечении трубопровода. Таким образом, в пристеночном слое жидкости температура полностью определяется подогревом внешней стенки. Нарушение подогрева очень быстро приведет к понижению температуры жидкости у стенки и повышению вероятности образования твердой фазы.
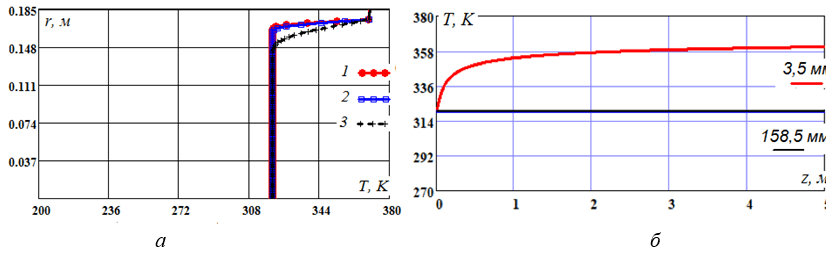
Рис. 5. а) Профиль температуры в различных сечениях трубопровода: 1) z=0,125 м; 2) z=0,288 м; 3) z=4,875 м; Исходные данные: L=5 м; λ = 0,11 Вт/м К; λc =15 Вт/м К; Ср=1380 дж/(кг К); б) Профиль температуры термоэластопласта в различных сечениях трубопровода
На рис. 5,б представлен профиль температуры термоэластопласта в различных сечениях трубопровода. Отметим быстрое изменение, в данном случае повышение, температуры в пристеночном слое жидкости.
Представляет интерес влияние на распределение температуры локальных дефектов в системе подогрева внешней стенки. Такие дефекты моделируются определением несимметричного распределения температуры внешней стенки трубопровода по длине (рис. 6).
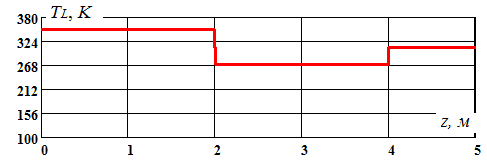
Рис. 6. Распределение температуры внешней стенки трубопровода по длине
На рис. 7, а показано распределение температуры по длине при наличии локального дефекта. Происходит достаточно быстрое падение температуры у стенки (в пристеночном слое). На рис. 7, б показано распределение температуры в различных сечениях трубопровода при наличии локальных дефектов теплоизоляции. Рисунок демонстрирует быстрое изменение профиля температуры в пристеночном слое. Представленные результаты подтверждают необходимость строгого соблюдения технологии подогрева внешней стенки трубопровода.
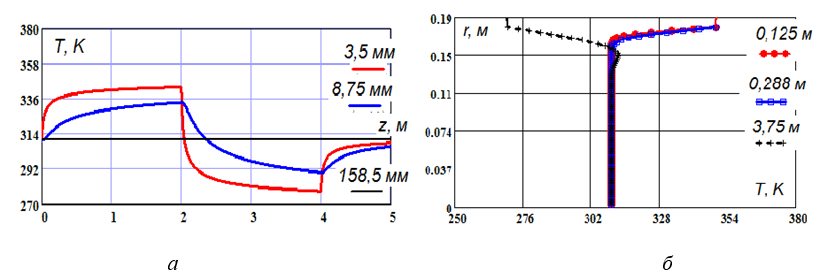
Рис. 7. а) Распределение температуры по длине трубопровода на различных расстояниях от стенки; б) Распределение температуры в различных сечениях трубопровода при наличии локальных дефектов теплоизоляции
Для тестирования предложенного алгоритма и компьютерной программы рассмотрена модельная задача. В модельной задаче правая часть уравнений составлена из условия определения точного аналитического решения начально-краевой задачи.
Уравнение теплопроводности для жидкости и стенки трубопровода приняты в виде:
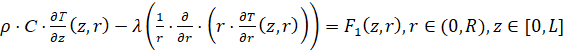 , (14)
, (14)
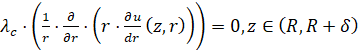 . (15)
. (15)
Начальные условия:
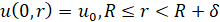 , (16)
, (16)
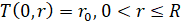 . (17)
. (17)
Краевые условия:
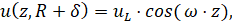
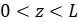 ,
,
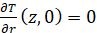 . (19)
. (19)
Условия сопряжения (жидкость-стенка):
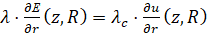 , (20)
, (20)
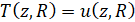 . (21)
. (21)
Условия (21)-(22) отражают непрерывность теплового потока и температуры на границе «жидкость-стенка». Правая часть уравнения (15) определяется из условия, что решение начально-краевой задачи имеет вид:
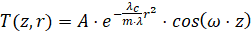 , (22)
, (22)
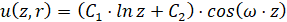 . (23)
. (23)
Результаты вычислений представлены на рисунок 8.
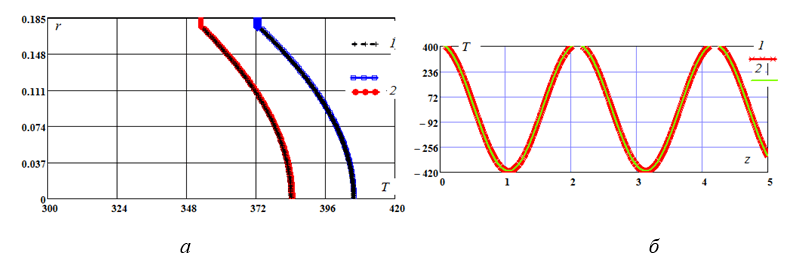
Рис. 8. а) Сравнение распределений температур по сечению на разной длине: 1 –приближенное решение; 2 – точное решение; б) сравнение температуры жидкости по длине трубопровода: 1 – приближенное решение; 2 – точное решение
Сравнение точного и приближенного решений краевой задачи позволяет выбрать рациональные значения параметров разностного метода.
Заключение
Сформулирована краевая задача с уравнением теплопроводности, краевыми условиями и условиями сопряжения. Решение задачи находится методом конечных разностей. Параметры метода конечных разностей определяются с помощью специальной модельной задачи.
Низкая теплопроводность жидкости и малая скорость потока (ламинарное течение) служит основанием учета передачи тепла к стенке трубопровода только теплопроводностью.
Получена оценка распределения температуры по сечению и по длине участка трубопровода при нарушении параметров подогрева наружной стенки трубопровода.

.png&w=640&q=75)