Понятия математического моделирования и его специфические особенности при решении задач на целые числа

Мы живём в постоянно обновляющемся мире: кардинально изменяются различные сферы жизнедеятельности, в том числе и образование. Поэтому наступает время активного внедрения инновационных образовательных технологий, основанных на совокупности интенсивных способов получения знаний и формирования развитой личности, умеющей думать, анализировать, а также творчески мыслить [4, c. 5-6].

Одной из задач математического образования учащихся является развитие логического мышления, которое является «фундаментом» любого мышления человека. Для решения этой задачи успешно используется важный метод научного познания и сильное средство активизации учебной деятельности – метод математического моделирования. Чаще всего данный метод применяется при решении текстовых задач, где краткая запись является графической моделью, а уравнение (выражение) – алгебраической моделью. Метод математического моделирования предполагает формирование абстрактного и логического мышления, развитие творческих способностей, умения мыслить, анализировать, обобщать и выделять основное. Данный метод является одним из наиболее доступных способов получения знаний.

Далее мы рассмотрим подробно данный метод.

Моделирование – процесс замещения объекта исследования его моделью и проведение исследований на модели с целью получения необходимой информации об объекте. В настоящее время данное понятие применяется во многих сферах жизнедеятельности.

Математическая модель – это приближённое описание какого-нибудь класса явлений, выраженное на языке какой-нибудь математической теории.

Основными признаками модели являются:

• некоторое объективное соответствие с познаваемым объектом;
• способность заменить его в определённом отношении;
• исследование модели даёт информацию о самом моделируемом объекте.

Моделирование – это процесс использования моделей для изучения тех или иных свойств оригинала. Например, чтобы доказать теорему Пифагора, катеты и гипотенузу временно заменяют буквами: a²+b²=c².

Исходя из вышесказанного, можно сформулировать цели моделирования:

• понимание устройства конкретной системы, её структуры, свойств, законов развития и взаимодействия с окружающим миром;
• управление системой, определение наилучших способов её изменения;
• прогнозирование результатов воздействия на изучаемую систему.

Использование метода математического моделирования предполагает следующие дидактические функции:

1. Познавательная функция (формирование познавательного образа изучаемого объекта).
2. Функция управления деятельностью учащихся.
3. Интерпретационная функция (описание одно и того же объекта с помощью различных моделей).

Применение нескольких функций математической модели способствует наиболее плодотворной деятельности учащихся и развитию их мышления.

Во введении понятий математическая модель и моделирование позволяют решать в учебном процессе следующие актуальные задачи:

• развитие мышления и интеллекта;
• формирование мировоззрения;
• овладение элементами математической культуры [6, c. 44-45].

Рассмотрим схему процесса математического моделирования:

1. Перевод предложенной задачи с естественного языка на математический (создание графической и алгебраической модели).
2. Решение задачи в рамках математической теории (внутри модели).
3. Перевод полученного результата (математического решения) на язык, которым была сформулирована исходная задача.

Самым сложным и ответственным является первый этап – само построение математической модели. Оно осуществляется логическим путём на основе глубокого анализа изучаемого процесса или явления и требует описать его свойства математическим языком.

Процесс создания модели можно описать пошагово:

1. Индуктивный: отбор наблюдений, относящихся к исследуемым свойствам объекта; принятие решения, что следует принимать во внимание, а чем можно пренебречь.
2. Построение неформальной модели: ищутся различные способы установления логического соответствия между моделью и объектом.
3. Перевод неформальной модели в математическую посредством математического языка и выбор подходящей математической структуры. Самый важный момент: выбранная модель может быть неоднозначной. При этом язык математики лишён двусмысленности и более точен, чем естественный язык.
4. Решение задачи в рамках математической теории. Здесь применяется весь набор математических методов – логических, алгебраических, геометрических.
5. Полученные результаты переводятся с математического языка обратно на естественный [6, с. 105-107].

Рассмотрим также проблемы, которые могут возникнуть у учащихся при решении текстовых задач.

Основная проблема состоит обычно в составлении математической модели. Она может быть представлена в форме уравнения, неравенства, диаграммы, графика, таблицы и т.д.

Для того пробы избежать этой проблемы, учащемуся нужно внимательно изучить и правильно растолковать данную ему текстовую задачу, а также связать искомые величины с известным.

Вторая проблема состоит в том, чтобы правильно составить систему уравнений или неравенств.

Третья проблема – это поиск решения (рационального) полученной системы уравнений или неравенств.

Рассмотрим на простом примере реализацию всех этапов процесса математического моделирования.

Задача №1. Длина земельного участка прямоугольной формы на 22 м больше ширины. Площадь участка составляет 1560 м². Найти длину и ширину земельного участка [3, c. 89].

Решение:

1. Первым этапом является создание математической и графической модели.

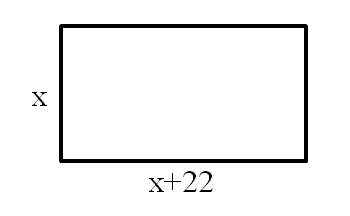
Пусть ширина земельного участка х м., тогда длина участка (x+22) м. Нам известно, что площадь прямоугольника равна S=a⋅b, следовательно, площадь участка составляет x∙(x+22) м² или 1560 м².

Составим и решим уравнение:

x∙(x+22)=1560 – это математическая модель данной задачи.

2. Второй этап включает в себя внутримодельное решение.

x∙(x+22)=1560;

x²+22∙x-1560=0;

D=22²-4∙1∙(-1560)=484+6240=6724;

;

;

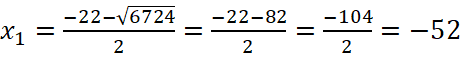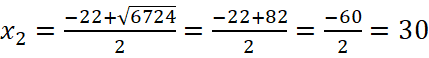3. Третий этап состоит в интерпретации результатов решения.

Ширина участка не может быть отрицательным числом, то есть x₁=-52 не является решением задачи, таким образом, ширина земельного участка 30 м, а длина участка 30+22=52 м.

Ответ: 30 м., 52 м.

Задача № 2. Вася знает четыре числа, сумма которых равна 99. Если первое число увеличить на 2, второе уменьшить на 2, третье умножить на 2, а четвёртое разделить на 2, то каждый раз получается одно и то же число [5]. Найдите эти четыре числа.

Решение:

1. На первом этапе создается математическая модель.

Здесь каждое из чисел обозначим за a, b, c, d. Нам известно, что сумма этих чисел равна 99, следовательно, a+b+c+d=99. Кроме того, известно, что если первое число увеличить на 2, второе уменьшить на 2, третье умножить на 2, а четвёртое разделить на 2, то каждый раз получается одно и то же число, следовательно, 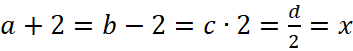, где x – некоторое постоянное число. Таким образом, выразив a, b, c, d соответственно, получим, a = x - 2, b = x + 2, c = x/2, d = 2∙x. А так как сумма этих чисел равна 99, получим финальное уравнение:

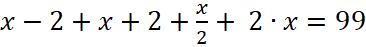 – это математическая модель данной задачи.

2. Второй этап включает в себя внутримодельное решение.

;

;

;

;

;

;

.

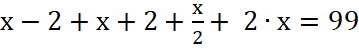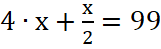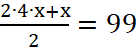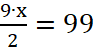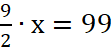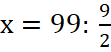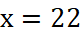3. Третий этап состоит в интерпретации результатов решения.

Так как x=22, тогда, соответственно, a=22-2=20, a=22+2=24,  c=22/2=11, d=22∙2=44.

Ответ: 20, 24, 11, 44.

Из вышесказанного можно сделать вывод, что за моделированием – будущее. Умение составлять математические модели сможет помочь в решении задач из различных отраслей науки, а также жизненных задач. Хочется отметить, что решение задач с применением моделирования активизирует мыслительную деятельность, помогает лучше понять задачу, самостоятельно найти рациональный путь ее решения, установить подходящий способ проверки, определить условия, при которых задача имеет (или не имеет) решения. Работа с моделью позволяет яснее увидеть зависимости между данными и искомыми величинами, оценить задачу в целом, продемонстрировать разные варианты решения.