Введение
Анализ развития военно-политической обстановки в мире, представленный в [2] свидетельствует о значительном повышении роли ПВО в вооруженных конфликтах. Это обусловлено развитием средств воздушно-космического нападения противника, а именно, развитие БПЛА. В статье [7] рассмотрены проблемы, возникшие у ПВО при поражении этих целей. «Учитывая, что скорости мини-БПЛА составляют порядка 50-250 км/ч, боевые расчеты этих ЗРК будут иметь достаточно времени на проведение предпусковых операций и обстрел цели. Тем не менее, стрельбы по мини-БПЛА показали низкую эффективность их поражения. Основными причинами при этом являются несовершенство системы управления подрывом боевой части ЗУР, а также большие ошибки сопровождения цели» – констатирует автор журнал «Военпред».
Для отражения от нападения с воздуха в современном мире активно применяется метод самонаведения ракет. Он используется в большинстве ракет, предназначенных для поражения подвижных целей, а также излучающих объектов (например, ракеты «Сайдуиндер», США; «Экзосет», Франция). Это самый точный способ наведения ракеты на цель. Особенно на цели с высокоманевренными характеристиками. Причем, чем дальше ракета удаляется от командного пункта, тем точнее и с меньшей ошибкой летит ракета. Или иначе, в процессе сближения ракеты с целью траектория промаха ракеты все время уменьшается [4]. В данной работе предложено использовать именно метод погони, не только потому что это один из самых точных методов наведения, помимо этого тут есть возможность настроить систему управления подрывом боевой части ЗУР.
Как работает самонаведение?
Самонаведение ракеты на цель – это такой метод управления, при котором сигнал управления вырабатывается на ракете в результате использования энергии, излучаемой целью или отраженной от нее [5]. На борту ракеты устанавливается специальная аппаратура управления, с помощью которой ракета сама определяет свое положение относительно цели и автоматически наводится на нее. Однако первоначально цель необходимо обнаружить по каким-либо характерным свойствам, отделив ее от окружающих предметов или, как говорят, от окружающего фона. К таким свойствам может быть отнесена прежде всего способность цели излучать или отражать электромагнитные колебания (радиоволны, видимые световые и невидимые инфракрасные лучи) иначе, чем окружающее ее пространство [6].
Для демонстрации работы построенной математической модели представлено исследование метода погони. С учётом высоких темпов развития средств воздушно-космического нападения требуется проводить моделирование для новых ракет и целей с более высокими характеристиками, и развивать способность к пониманию и разработке математических моделей у курсантов учебных заведений ВКО (воздушно-космической обороны).
Говоря о методе наведения, мы подразумеваем закон сближения ракеты с целью, который в зависимости от координат и параметров движения цели определяет требуемое движение ракеты, обеспечивающее попадание ракеты в цель. Методом погони называется такой метод наведения, при котором в каждый момент времени вектор скорости ракеты направлен на цель.
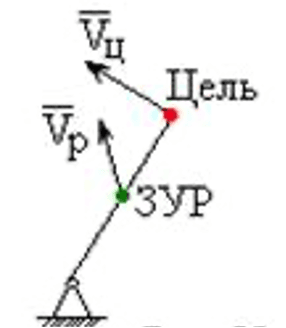
Рис. 1. Метод погони
Одним из средств, позволяющих решить задачу реализации модели метода погони, является использование программной среды C#. Она позволяет задать параметры движения ЗУР (зенитно-управляемой ракеты) и цели, построить траекторию ракеты, решить целый ряд связанных с данной моделью задач. Например, так как исследуемая математическая модель позволяет определять возникающие в ходе движения ракеты перегрузки, мы можем определить границы зоны поражения зенитного ракетного комплекса [3].
При построении модели будет использован упрощенный принцип наведения, так называемый «метод контрольных сумм». Предложенный метод не требует решения сложный дифференциальных уравнений, а основан на системе простых неравенств. Это позволяет сделать процесс моделирования легче и доступнее, сохраняя при этом сущность данного метода.
Моделирование наведения ЗУР методом погони
Весь процесс наведения ракеты ближнего действия длится несколько десятков секунд. За это время ракета должна успеть искривить свою траекторию. Следовательно, инерционность ракеты должна быть мала. Особенно это важно при наведении на быстродвижущиеся самолеты и маневрирующие цели. Резкий манёвр, совершаемый в определенный момент времени самолетом, может вызвать недопустимую ошибку наведения, в случае большой инерционности СУ ракетой. Таким образом, переходный процесс h(t) в относительных единицах будет выглядеть, как показано на рисунке 2 [1].
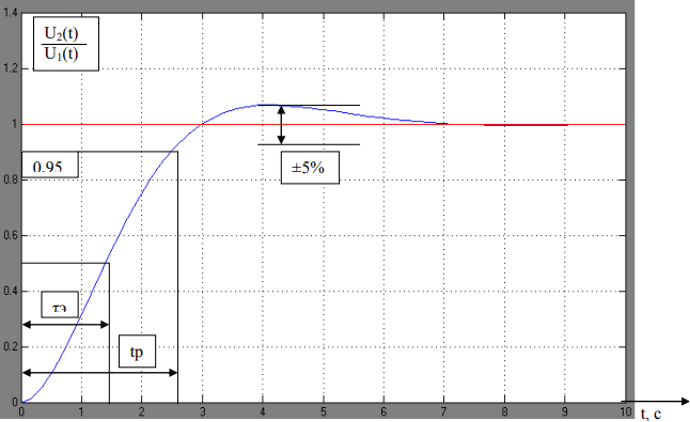
Рис. 2. Изображение переходного процесса в системе управления ракеты
Рассмотрим идеализированный случай, когда головка самонаведения моментально реагирует на изменение параметров движения цели. Предложенный способ реализации метода погони заключается в следующем:
1. Нам всегда известно положение цели относительно ракеты, а, следовательно, известна линия визирования и её параметры (в том числе и длина этой линии).
2. В каждый момент времени модель ЗУР исследует пространство в определённом секторе, где может находиться цель, путём построения линии сканирования на расстоянии 6 условных единиц от ракеты.
double ctr1x = xf + 6;
double ctr1x = xf + 6;
double ctr1y = yf;
double ctr2x = xf + 5;
double ctr2y = yf + 1;
double ctr3x = xf + 4;
double ctr3y = yf + 2;
double ctr4x = xf + 3;
double ctr4y = yf + 3;
double ctr5x = xf + 2;
double ctr5y = yf + 4;
double ctr6x = xf + 1;
double ctr6y = yf + 5;
double ctr7x = xf + 0;
double ctr7y = yf + 6;
double ctr7y = yf + 6;
xf, yf – координаты ЗУР на плоскости
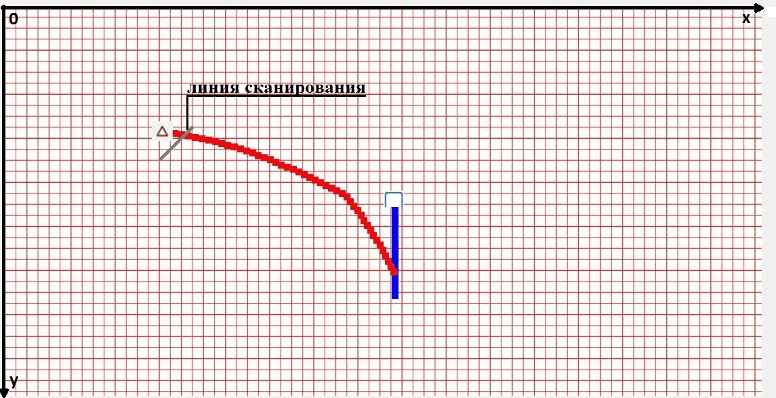
Рис. 3. Представление линии сканирования
3. Затем находим расстояние от ЗУР до исследуемой точки на линии сканирования и от исследуемой точки до положения цели. Полученные значения суммируются.
double ztctr1 = Math.Round(Math.Sqrt(Math.Pow(ctr7x - xf, 2) + Math.Pow(ctr7y - yf, 2)));
double ctr1te = Math.Round(Math.Sqrt(Math.Pow(ctr7x - xe, 2) + Math.Pow(ctr7y - ye, 2)));
double csum1 = ztctr1 + ctr1te;
Данная операция проводится со всеми исследуемыми точками. Из полученных контрольных сумм выбирается минимальная. Результат говорит о том, что исследуемая точка лежит на линии визирования.
double itog = csum.Min();
if(itog==csum1)
{
dxf = 0;
dyf = 6;
}
if (itog == csum2)
{
dxf = 1;
dyf = 5;
}
.
.
if (itog == csum7)
{
dxf = 6;
dyf = 0;.
4. Перемещаем модель ракеты в точку, лежащую на линии визирования.
xf += dxf;
yf += dyf;
pictureBox2.Location = new Point(xf, yf);
Вид программы представлен на рис. 4
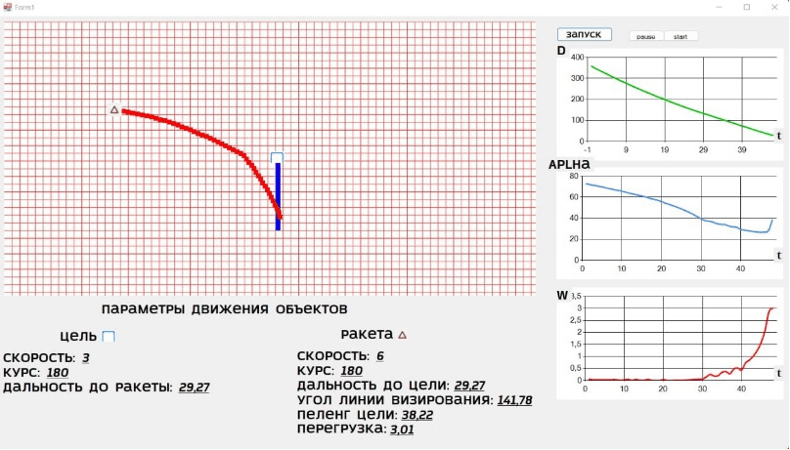
D – длина линии визирования; APLHA – угол между направлением на север и направлением на цель; W – величина кинематической перегрузки
Рис. 4. Вид программы
Таким образом, модель ракеты будет двигаться по линии визирования в каждый момент времени. Программа позволяет измерять кинематические перегрузки, что позволяет рассчитать зону поражения ракеты в различных условиях. В результате исследований очевидно, что перегрузка ракеты максимальна в момент предельного сближения ЗУР с целью, это позволяет настроить систему управления подрывом боевой части ракеты в этот момент, что решает проблему уничтожения БПЛА, представленную в статье [4].
Выводы
Проведённое нами исследование показывает, что использование программной среды С# позволяет построить упрощённую модель работы ЗУР по цели движущейся равномерно и прямолинейно, используя метод погони. Предложенный упрощённый алгоритм также позволяет строить модели с непостоянными параметрами движениями цели и имеет большой потенциал для исследования, что может быть использовано курсантами вузов ВКО.
Этот метод в перспективе может успешно применяться при разработке ЗРК против беспилотных летательных аппаратов. Актуальность данной разработки ярко показал опыт проведения СВО на Украине.

.png&w=640&q=75)