Перспективы применения методов искусственного интеллекта в контексте ДВ-УФО моделирования социально-экономических систем

Цифровая экономика (ЦЭ), начинавшаяся более тридцати лет тому назад с автоматизации бухгалтерского и складского учёта, в настоящее время обрела научный и технологический потенциал, достаточный для коренной перестройки не только отдельных направлений экономической деятельности, но и экономики в целом. Это означает, в том числе, необходимость постепенного, но необратимого перехода от вербальных экономических моделей с элементами математики и компьютерных информационных технологий к цифровым моделям (ЦМ) социально-экономических систем (СЭС).

Для уточнения терминологии определим понятие СЭС максимально узко: как систему, элементами которой являются социальные институты, юридические и физические лица, взаимодействующие по поводу получения, перераспределения и переработки ресурсов. Задача разработки ЦМ даже сравнительно простых СЭС является весьма сложной, и в настоящее время её сколько-нибудь удовлетворительное решение отсутствует. Однако данная проблематика находится в фокусе внимания исследователей и практических работников, что в сочетании с прогрессом в области компьютерных информационных технологий и искусственного интеллекта (ИИ) даёт положительные результаты.

Необходимо отметить, что применение компьютерных информационных технологий и методов ИИ должно быть экономически оправданным. В рамках ЦЭ будут востребованы только те технологии, которые способны приносить прибыль. Поэтому методы разработки ЦМ должны не только позволять создавать точные и адекватные модели СЭС, но и делать это с минимальным потреблением ресурсов.

Практиками в области менеджмента давно установлено эмпирическое правило: 20% первоначальных затрат дают 80% результата. Поэтому вполне оправдано возрождение интереса к так называемым «минимальным» моделям СЭС, в которых задачи анализа ставятся предельно узко и конкретно, что даёт возможность применения простых специализированных алгоритмов. Методы построения подобных ЦМ не потребляют значительных ресурсов, поэтому они могут применяться не только в крупных, но и в средних и малобюджетных проектах.

Понятие «минимальной» модели весьма неопределенно, поэтому в дальнейшем будем под этим термином понимать ЦМ, которая может быть реализована с использованием монетарного (денежного) представления ресурсов. Помимо монетарного представления, возможно натуральное и индексное описание ресурсов. Однако только монетарное представление ресурсов (в силу известной функции денег как меры товаров и услуг) является универсальным и открывает возможность для построения ЦМ СЭС, ориентированных на этап инстанцирования инвестиционных проектов (так называемая фаза 0).

На этапе инстанцирования методы проектного и предпроектного анализа не работают, поскольку на этом этапе в ходе переговоров инвесторов происходит постановка целей и задач проекта, а также из инвесторов и других заинтересованных лиц формируется производственная СЭС, для реализации проекта. Вследствие этого, фаза 0 инвестиционного проекта стала в последнее время объектом интенсивных исследований, и предприняты многочисленные попытки разработки методов моделирования фазы 0.

В русле этой тенденции была осуществлена специализация системного подхода «Узел-Функция-Объект» (УФО подход) к задаче построения минимальных ЦМ СЭС. Отличительными чертами нового метода являются: ориентация на фазу 0, использование только монетарного описания ресурсов, отказ от использования применяемых в УФО методе сложных для понимания и восприятия исчислений Гренандера, Милнера и Абади-Кардели [2], и замена их простой графической нотацией и адаптированной к потребностям объектно-ориентированного программирования (ООП) знаковой системы, применяемой в финансовой математике.

В результате разработан метод (ДВ-УФО метод) построения минимальных ЦМ СЭС, которые являются дискретно-событийными моделями (ДСМ), по своей сути аналогичными моделям системной динамики Форрестера. Принадлежность ДВ-УФО моделей к классу ДСМ значительно облегчает реализацию инструментария компьютерной поддержки ДВ-УФО моделирования.

Поскольку ДВ-УФО метод ориентирован на использование в узких предметных областях, чтобы не выполнять специализацию для каждой предметной области с нуля, специализация осуществляется в два шага. Было выделено стабильное ядро ДВ-УФО метода, предназначенное для моделирования произвольных финансовых систем, а на втором шаге стабильное ядро (базовая редакция ДВ-УФО метода) адаптируется к потребностям специалистов конкретной предметной области [3, 4]. Разработана методика адаптации базовой редакции, которая универсальна для любой предметной области и которая сводится к простому расширению отдельных компонент ДВ-УФО модели.

На рис. 1 представлена архитектура ДВ-УФО модели, инвариантная к предметной области.

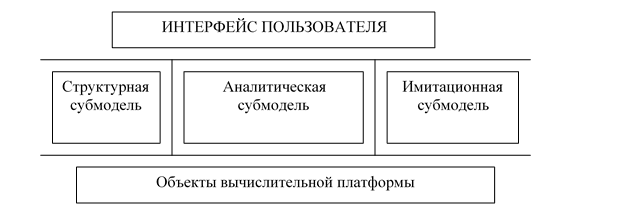
Рис. 1. Архитектура ДВ-УФО модели

Архитектура ДВ-УФО модели включает структурную, аналитическую и имитационную субмодели. Структурная субмодель содержит описание элементов финансовой системы и существующих между ними связей. Имитационная субмодель обеспечивает поддержку экспериментов, наиболее важным из которых является эксперимент, осуществляющий валидацию финансовой системы. Аналитическая субмодель инкапсулирует декларативные и процедурные знания о предметной области.

В целом, ДВ-УФО метод отвечает требованиям сегодняшнего дня, удовлетворительно справляясь с моделированием финансовых инструментов, анализом инвестиционных проектов, а также моделированием в тех предметных областях, где главную роль играет финансовая подсистема. Однако для применения в контексте ЦЭ ДВ-УФО метод требует ряда усовершенствований, связанных с повышением надёжности и адекватности ДВ-УФО моделей.

Рассмотрим вопросы надёжности и адекватности ДВ-УФО моделей подробнее. Последовательность создания ДВ-УФО модели следующая: сначала создаётся структурная субмодель, затем заполняется информационная база аналитической субмодели, после чего выполняются имитационные эксперименты. На каждом из этих этапов разработчик ДВ-УФО модели может внести в модель ошибку, которая, если её не обнаружить и вовремя не исправить, полностью дискредитирует модель и сделанные на её основе выводы. На рис. 2 представлена структурная диаграмма ипотеки с кредитованием первоначального взноса.

Структурная диаграмма ипотеки на рис. 2 выполнена в базовой редакции ДВ-УФО метода, в которой нотация содержит только 4 терминальных знака: окружности – для репозиториев, спонсоров и абсорберов, а также стрелки – для финансовых потоков. Диаграмма содержит всего 4 узла и 4 стрелки. При построении столь простой структурной диаграммы трудно ошибиться. Однако, если узлов и финансовых потоков более десятка, то возможность ошибочного создания финансового потока резко возрастает.

Базовая редакция предоставляет примитивный способ контроля правильности создания финансовых потоков, вытекающий из семантики и прагматики графической нотации. Технически это реализуется с помощью матрицы смежности для терминальных элементов структурной диаграммы, если её рассматривать как ориентированный граф. В таблице представлена матрица смежности для терминальных знаков базовой редакции. Строки в ней соответствуют источнику финансового потока, а столбцы – приемнику. Так строка, соответствующая финансовому поглотителю – абсорберу целиком состоит из нулей, что отражает тот факт, что абсорбер только выводит деньги из финансовой системы, но поступать в систему деньги через него не могут.

Таблица

Матрица смежности для терминальных знаков базовой редакции

В свою очередь, данные столбца А показывают, что получить финансовый поток абсорбер может только от репозитория.

В целом матрица смежности отражает тот простой факт, что обмениваться финансовыми потоками могут только репозитории. Как показала практика ДВ-УФО моделирования, в моделях, построенных с применением базовой редакции, столь слабой формы контроля вполне достаточно для адекватного представления структуры финансовой системы. Но, если моделирование осуществляется в расширенной редакции, адаптированной к предметной области, в которой не все репозитории могут обмениваться финансовыми потоками, то использование матрицы смежности может легко привести к ошибкам в построении структурной субмодели.

Очевидно, что промышленные ДВ-УФО модели, применяемые в контексте ЦЭ, подобных ошибок не должны содержать в принципе. Исправить положение потенциально можно с помощью деления ролей: роль репозитория в конкретной прикладной области разбивается на несколько подролей, и для новых ролей вводятся знаки новых терминальных элементов и строится матрица смежности большей размерности, лучше контролирующая ситуацию. Подобный подход прост, но крайне не эффективен, поскольку после деления ролей требуется модернизировать инструменты компьютерной поддержки ДВ-УФО моделирования.

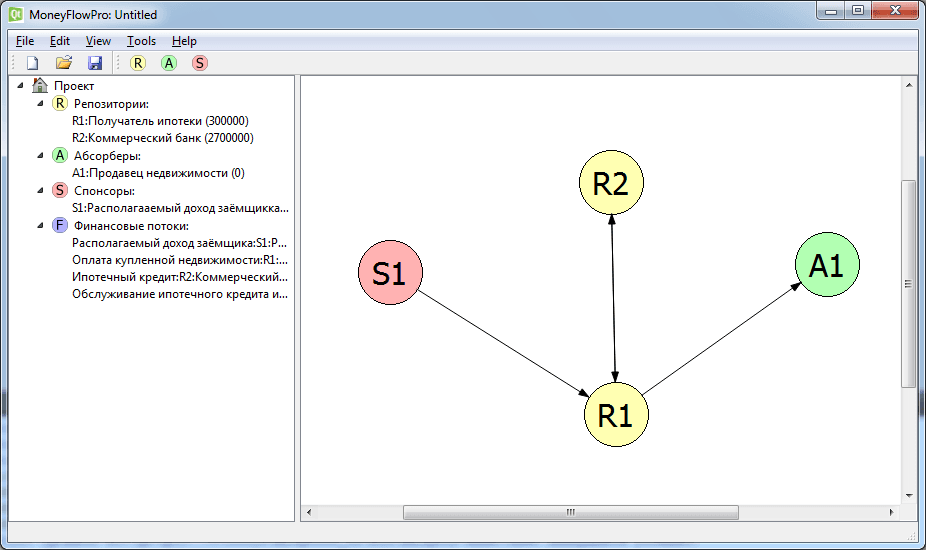
Рис. 2. Структурная диаграмма ипотеки

Единственный рациональный выход из этой тупиковой ситуации – сделать инструментарий компьютерной поддержки ДВ-УФО моделирования «умнее» за счёт внедрения в него подходящих методов ИИ. В настоящее время разработано много различных методов и алгоритмов ИИ. Часто задачу можно решить несколькими альтернативными методами.

Для контроля правильности построения ДВ-УФО диаграммы достаточно внедрения в инструмент компьютерной поддержки ДВ-УФО моделирования простой экспертной системы, которая бы на основе экспертных знаний о предметной области, контролировала бы ход построения структурной субмодели. При этом, сама экспертная система, пройдя обучение, в дальнейшем работала бы в фоновом режиме, вмешиваясь в действия разработчика ДВ-УФО модели по мере необходимости. Наличие интерфейса обучения, позволяет при необходимости провести переобучение. Реализация подобного подхода не вызывает затруднений, поскольку для представления знаний в данной задаче можно использовать продукционные правила [1, с. 175].

Если структурная субмодель СЭС построена правильно, то можно переходить к созданию аналитической субмодели. Эта субмодель содержит декларативные знания о моделируемой СЭС, инкапсулированные в виде множества траншей (событий перемещения денежных средств) и значений начальных балансов элементов ДВ-УФО диаграммы. Помимо декларативных аналитическая субмодель базовой редакции содержит процедурные знания о методах проведения NPV и IRR анализа; расширенные редакции могут содержать и другие аналитические процедуры. В частности, может потребоваться генерация траншей в автоматическом режиме.

В базовой редакции предусмотрена генерация только постоянных рент с заданным на некоторый момент времени текущим значением PV (Present Value). Этого достаточно для инкапсуляции достоверных декларативных знаний о простейших видах финансовых операций (краткосрочный кредит, ипотека и т.п.). Кроме того, автоматическая генерация траншей необходима для работы в реальном масштабе времени. Легко в режиме диалога ввести транш получения ипотечного кредита, но ввести в таком же режиме несколько десятков траншей, идущих на погашение ипотечного кредита, и не легко, и чревато внесением в модель трудно обнаруживаемых ошибок. Очевидно, что погасительные транши должны генерироваться автоматически, на основании имеющейся в модели информации об ипотеке.

Понятно, что при автоматической генерации траншей проблема ошибок не устраняется, а переходит на другой уровень: разработчик ДВ-УФО модели может неверно выбрать метод генерации траншей. Очевидно, что и здесь требуется участие экспертной подсистемы контроля генерации траншей. Ключевым моментом в этом случае является способность подсистемы контроля идентификации ситуации, а не запрос к разработчику о его намерениях, на который тот может ответить не точно либо совсем неверно.

Среди методов ИИ достаточно средств решения данной проблемы, например сети Кохонена, но существуют и другие подходы [1, с. 85]. Выбор наиболее подходящего из них является содержанием исследований. Однако без успешного решения проблемы автоматической генерации траншей трудно ожидать широкого применения ДВ-УФО моделей в контексте ЦЭ.

После создания структурной и аналитической субмоделей появляется возможность проведения с ДВ-УФО моделью различных экспериментов для изучения характеристик и определённых аспектов поведения СЭС. Основным имитационным экспериментом, присутствующим уже в базовой редакции ДВ-УФО метода, является эксперимент по валидации СЭС, т.е. по проверки СЭС на выполнимость. Очевидно, что СЭС валидна, если все элементы СЭС в состоянии в течение всего времени жизни СЭС выполнять свои обязательства. Более конкретно: все элементы СЭС способны оплачивать потребляемые ресурсы и у них достаточно оборотных средств для ведения экономической деятельности.

В базовой редакции транш определяется как объект, содержащий ответы на кортеж вопросов:<Кто?, Кому?, Когда?, Сколько?, Основание?>. Для проведения NPV и IRR анализа основное значение имеет пара (t, x), отвечающая на вопросы «Когда?» и «Сколько?». В настоящее время ДВ-УФО моделирование осуществляется в предположении, что значения пары (t, x) всегда точно определены в виде конкретного момента календарного времени и действительного числа. В реальных ситуациях это предположение может не выполняться. Оплата ресурса обычно допускается в течение некоторого интервала времени (например, в течение месяца после покупки). Спонсор также может выразить свои намерения не точно (например, выделить средства в пределах некоторой суммы).

Во всех подобных случаях приходится иметь дело с нечёткой (не путать со случайной) информацией. Методы ИИ, разработанные Лофти Заде и другими исследователями [1, с. 210], позволяют находить решение проблемы нечёткости информации. Инструменты компьютерной поддержки ДВ-УФО моделирования должны предоставлять возможность работы с нечёткой информацией, по крайней мере, с нечётким заданием времени прихода транша.

Рассмотренные проблемы ДВ-УФО моделирования показывают, что без широкого применения методов ИИ невозможно создавать промышленные методы моделирования СЭС, пригодные для использования в контексте ЦЭ. Вместе с тем, нельзя не отметить, что и УФО метод, и его специализированная редакция ДВ-УФО метод хорошо взаимодействуют с методами ИИ, позволяя создавать инструменты моделирования, отвечающие требованиям ЦЭ [5].

Работа поддержана грантом РФФИ №18-07-00310а.