Олимпиада «Шаг в будущее» по математике для 8 класса. Очный тур

В статье представлены два варианта заключительного этапа межрегиональной олимпиады «Шаг в будущее» по математике для 8 классов. Задачи различных типов затрагивают большинство тем школьной программы, позволяют ученику проявить себя с помощью разных способов рассуждений, не терять интереса к процессу решения. Задачи расположены в порядке нарастания уровня сложности. Надеемся, что материал статьи будет полезен школьникам и их наставникам.

Вариант 3

1. (10 баллов) В кастинге передачи «Последний герой» участвовали 90 человек, им было предложено 4 испытания. Первое из них успешно прошли 70 человек, второе 40, третье 85 и четвертое 75. Но все испытания не прошел никто. Найдите количество прошедших в следующий тур, если в следующий тур вышли участники, преодолевшие и третье, и четвертое испытания.
2. (15 баллов) Пусть 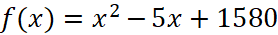. Решите уравнение .
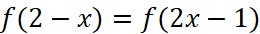3. (15 баллов) В выпуклом четырехугольнике ABCD AB = 12, CD = 15. Диагонали AC и BD пересекаются в точке O, AC = 18, треугольники AOD и BOC имеют равные площади. Найдите AO.

4. (20 баллов) При каких значениях параметра а уравнение 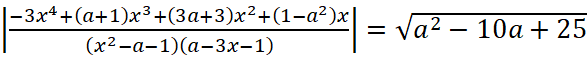  имеет одно решение?

5. (20 баллов) В прямоугольном треугольнике АВС с гипотенузой АВ, равной 8 см, высота, проведенная к гипотенузе, равна 2 см. Найдите острые углы треугольника. Ответ дайте в градусах.
6. (20 баллов) Даны 10 натуральных чисел, сумма любых четырёх из них чётна. Может ли произведение всех десяти чисел оканчиваться на 2020? Ответ обоснуйте.

Решения олимпиады. 8-й класс. Вариант 3

1  Первое и второе испытания прошли минимум 70 + 40 - 90 = 20 человек. Третье и четвертое минимум 85 + 75 – 90 = 70 человек. Но никто не прошел все испытания, значит, первое и второе прошли 20 человек, третье и четвёртое – 70. Ответ: 70 человек.

2. Пусть уравнение имеет вид 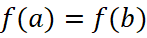  получаем что: 

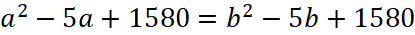
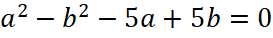
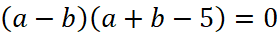
Произведение двух множителей равно нулю, если хотя бы один из множителей равен нулю. Следовательно, a=b или a+b=5.

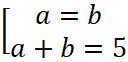
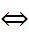
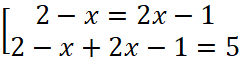
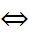
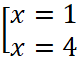
Ответ: {4; 1}.

3. Из равенства площадей треугольников AOD и BOC (рис. 1) и равенства углов (∠AOD=∠BOC) следует 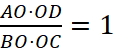 (теорема об отношении площадей треугольников, имеющих по равному углу). Откуда получаем, что 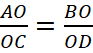. При этом ∠AOB=∠DOC как вертикальные. Следовательно треугольники AOB и COD подобны. 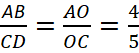, а значит АО=8.

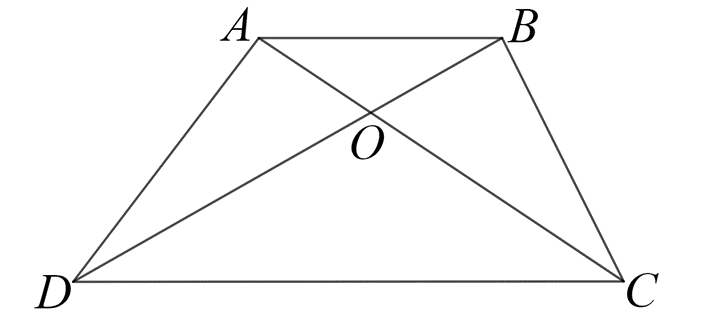
Рис. 1. Чертеж к задаче 3

Ответ: 8.

4. Преобразуем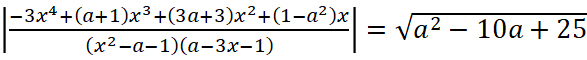   

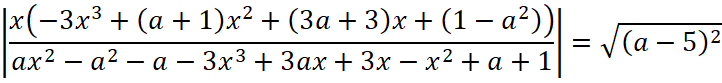
Решим графически уравнение 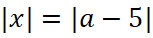, a≠x²-1, a≠3x+1, в системе xOa.

То есть 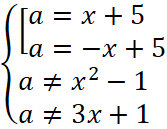(рис. 2).

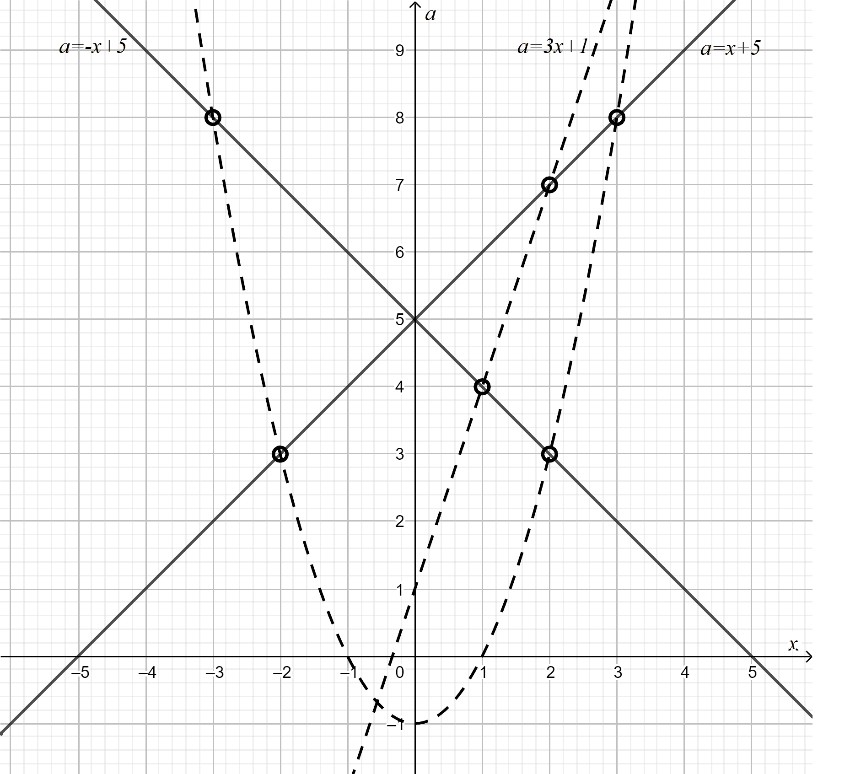
Рис. 2. График к задаче 4

Ответ: при а = 4, а = 5, а = 7.

5. Проведем высоту СН (рис. 3) и медиану СК. По свойству медианы прямоугольного треугольника СК=АК=КВ=0,5АВ=4 см. Треугольник СКН прямоугольный, так как СН – высота. СН = 2 см, СК = 4 см, тогда угол СКН = 30^о (по свойству катета в прямоугольном треугольнике). Треугольник СКВ – равнобедренный, так СК=КВ. Тогда по свойству углов равнобедренного треугольника 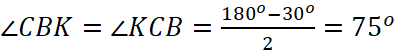. В треугольнике .

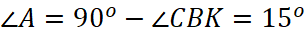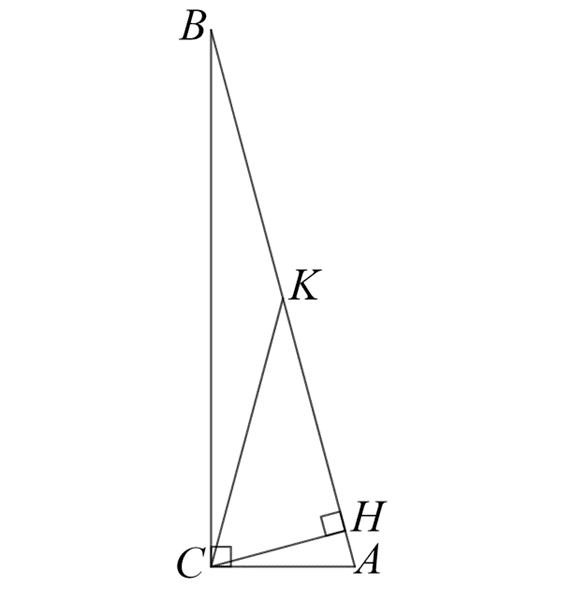
Рис. 3. Чертеж к задаче 5

Ответ: 15°, 75°.

6. Очевидно, что чётность всех чисел одинакова. В противном случае, если есть числа с разной чётностью, то чисел хотя бы одной из этих чётностей хотя бы 3 (по принципу Дирихле), в таком случае, мы можем взять эти 3 числа и 1 число другой четности, и сумма этих четырех числе не будет чётной. Но если все они нечётные, то произведение нечётно, а если чётные, то делится на 2¹⁰. Однако число, которое кончается на 2020, делится на 4, но не делится на 8.

Ответ: нет.

Вариант 4 (для самостоятельного решения)

1. (10 баллов) Творческий конкурс в институт состоял из четырех заданий. Всего абитуриентов было 70 человек. Первое испытание успешно выдержали 35, второе 48, третье 64, четвертое 63 человека, при этом все 4 задания не выполнил никто. Прошедших и третье, и четвертое испытания зачислили в институт. Сколько было зачисленных?
2. (15 баллов) Пусть 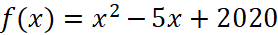. Решите уравнение .
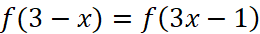3. (15 баллов) В выпуклом четырехугольнике ABCD AB = 10, CD = 15. Диагонали AC и BD пересекаются в точке O, AC = 20, треугольники AOD и BOC имеют равные площади. Найдите AO.

4. (20 баллов) При каких значениях параметра а уравнение 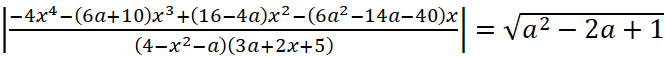   имеет одно решение?

5. (20 баллов) В выпуклом четырехугольнике АВСD ∠B=∠D=90^o, диагонали АС и BD взаимно перпендикулярны, а диагональ АС является биссектрисой углов А и С. Найдите углы А и С, если АС = 2BD. Ответ дайте в градусах.
6. (20 баллов) Даны 10 натуральных чисел, сумма любых четырёх из них чётна. Может ли произведение всех десяти чисел оканчиваться на 1580? Ответ обоснуйте.