До рассмотрения предлагаемой технологии оптимизации использования ограниченных ресурсов, обеспечивающих жизненные циклы всевозможных предметов, условимся под предметом здесь и далее понимать имеющее определенные свойства, одушевленное и неодушевленное материальное (неорганической природы и живое), абстрактное, материально-абстрактное, любое из того, что нас окружает, что нами создается, что служит объектом или источником какой-либо деятельности, какого-либо состояния или отношения, что служит содержанием мысли, речи, а под потенциалом предмета – величину способности этого предмета выполнять заданные функции, соответствовать своему предназначению, степень возможного проявления какого-либо действия.
Если арифметические процессы сложения и умножения потенциалов элементов структуры предмета удается провести в обратном порядке, то устанавливаются количественные отношения между выявленными слагаемыми и перемножаемыми величинами таких элементов. Например, потенциал системы управления можно представить равным произведению потенциалов сил связи и сил управления, так как если любой из этих потенциалов упадет до нуля, то и потенциал системы управления, естественно, тоже упадет до нуля. Другой пример: потенциал сил бригады землекопов равен сумме потенциалов сил всех землекопов бригады потому, что если потенциал сил одного землекопа упадет до нуля, то потенциал сил бригады уменьшится, но не упадет до нуля. Кроме того, очевидно, что потенциал любого предмета будет уменьшаться в зависимости от степени взаимозависимости потенциалов его элементов. Поэтому и произведение и сумму потенциалов элементов при раскрытии структуры потенциала предмета необходимо умножать на коэффициенты взаимозависимости элементов предмета. Эти безразмерные коэффициенты в зависимости от степени взаимозависимостей потенциалов элементов принимают величину в интервале от единицы до нуля и равны единице, если взаимозависимость отсутствует, или нулю, если взаимозависимость полная.
Выявление в анализируемом предмете полной группы его элементов, отвечающих указанным выше условиям, определяется интеллектом анализирующего или конструирующего предмет специалиста, который каждый элемент предмета рассматривая в качестве более простого предмета раскрывает структуру его и его элементов до тех пор пока размерность элементов не станет одномерной. При этом структура исходного предмета раскрывается в виде многоэтажной пирамиды. Удобный для рассмотрения вид такой структуры представлен на рисунке 1. На нем элементы, потенциалы которых перемножаются, изображаются в виде прямоугольников, а потенциалы которых складываются – эллипсами. Символы "U" означают потенциал предмета или его элемента, символы "f" – коэффициенты взаимозависимости элементов.
Характер структуры одного и тог же предмета может иметь несколько вариантов (экономический, производственный, эксплуатационный и т.д.).
Подводя итог проведенному анализу арифметических сложения и умножения, можно сформулировать правила построения структуры предмета различной природы и сложности и расчета соотношений потенциалов его элементов ‒ тектологическую функцию [1]:
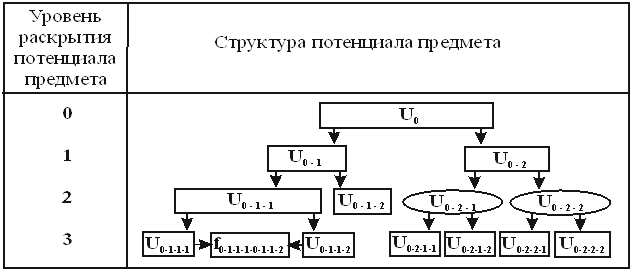
Рис. 1. Структура потенциала некоторого предмета, раскрытая по правилам тектологической функции
Правило I: Если предмет может быть полностью и непосредственно определен (описан, охарактеризован) несколькими элементами (свойствами, характеристиками), увеличение потенциала (величины) каждого из которых ведет к увеличению потенциала предмета, а стремление к нулю – лишает его смысла, предназначения, обращает в нуль, то потенциал предмета равен произведению потенциалов этих элементов и потенциалов (коэффициентов) взаимозависимости всех пар элементов
U0 = 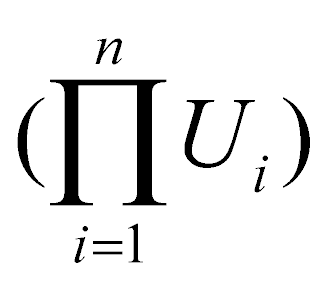 ٠
٠ 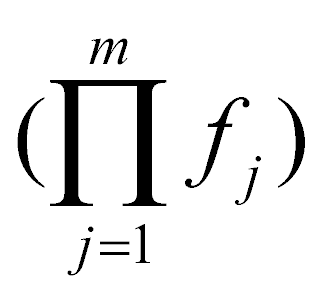 , (1)
, (1)
где n – количество указанных элементов потенциала предмета, m – количество потенциалов (коэффициентов) взаимозависимости fj всех пар элементов, Ui – потенциал i-го элемента структуры потенциала предмета. Если такие элементы определяются другими элементами, а те своими и так далее несколько раз, и все они отвечают изложенному выше правилу, то потенциал такого предмета равен произведению потенциалов элементов (Uk.i), завершающих раскрытие структуры потенциала предмета и коэффициентов взаимозависимости fj всех пар элементов всех уровней структуры потенциала предмета
U0 = 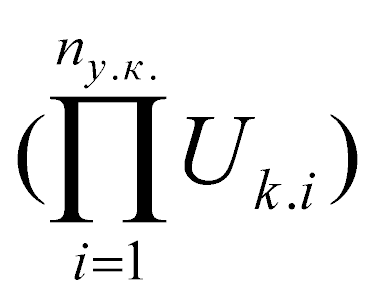 ٠
٠ 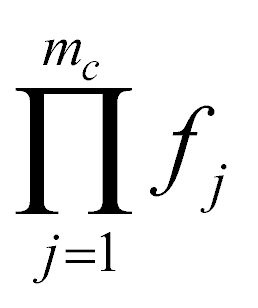 (2)
(2)
где nу.к. – количество, завершающих раскрытие всех ветвей структуры потенциала предмета U0 и отвечающих требованиям правила I, Uk.i – потенциал i-го элемента, завершающего раскрытие структуры потенциала предмета; mc – количество потенциалов (коэффициентов) взаимозависимости fj всех пар элементов всех уровней структуры потенциала предмета. Коэффициенты fj могут принимать значения от нуля до единицы (при отсутствии стремится к единице, при полной взаимозависимости – к нулю).
Правило II: Если предмет может быть полностью и непосредственно определен (описан, охарактеризован) несколькими элементами (свойствами, характеристиками) (Uk) с одинаковой размерностью, увеличение потенциала (величины) каждого из которых ведет к увеличению потенциала (величины) предмета, а стремление к нулю уменьшая потенциал предмета не меняет его смысл, предназначение и не обращает в нуль, то потенциал такого предмета (U0) равен сумме потенциалов всех его элементов Uk, умноженной на произведение потенциалов (коэффициентов) взаимозависимости всех пар элементов потенциала предмета
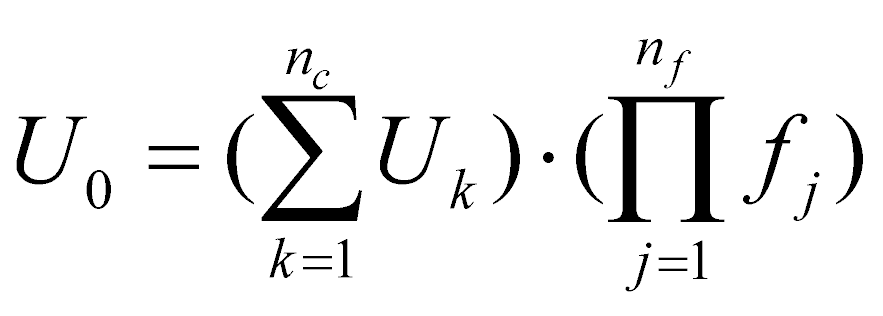 , (3)
, (3)
где nс – количество элементов, отвечающих требованиям правила II.
Правило III: Если коэффициенты ki не зависят от величины средств, выделяемых элементам предмета, когда эти средства близки к оптимальной величине, то оптимальная по критерию качество/цена предмета доля ресурсов (средств), выделяемых элементам, выявленным по правилам I тектологической функции и завершающим полное раскрытие всех ветвей структуры потенциала предмета, кроме безразмерных, получается в результате равномерного распределения всех средств (ресурсов) между ними. Если в структуре потенциала предмета имеют место ее фрагменты, раскрытые по правилам II тектологической функции, то оптимальное распределение ресурсов между такими элементами определяется отдельным расчетом. Здесь ki – коэффициент пропорциональности между потенциалом i-го элемента и средствами (ресурсами) Pi, обеспечивающими его жизненный цикл.
Из первого правила вытекает следствие: При наличии отклонений от оптимального распределения средств (ресурсов) между элементами потенциала предмета, выявленными по правилу I, его относительный потенциал (отношение имеющего место в данном случае потенциала предмета к его потенциалу при оптимальном распределении средств между всеми его элементами)
U00.p. = U0 / U0.макс. = 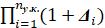 , (4)
, (4)
где Di = (Ui – Ui.опт.) / Ui.опт. = (Рi – Рi.опт.) / Рi.опт.. При этом очевидно, что сумма всех отклонений Δi равна нулю.
Из выражения (4) следует, что относительный потенциал предмета, структура которого отвечает правилу I, не зависит от коэффициентов ki и fj и поэтому удобен для анализа влияния на него отклонений от оптимального распределения средств (ресурсов) между его элементами.
Относительный потенциал U00.Р. подобен прочности физической цепи, состоящей из звеньев с прочностью, эквивалентной (1 + Δi). Средства Pk.i эквивалентны массе звена цепи. Чем больше разброс по массе (толщине) звеньев, тем ниже возможной прочность всей цепи, определяемой самым слабым звеном, ниже эффективность использования ограниченных средств, обеспечивающих жизненный цикл предмета.
Используя выражение 4, с помощью специальной компьютерной программы построена зависимость величины потенциала предмета от отклонений от оптимального распределения ресурсов, обеспечивающих его жизненный цикл (рисунок 2). Обращает на себя внимание крайне высокая крутизна этой зависимости для сложных систем (продуктов). Ничтожное уменьшение величины указанных отклонений приводит к существенному увеличению величины потенциала (качества) предмета при сохранении величины ресурсов, обеспечивающих жизненный цикл предмета. Упомянутая программа облегчает разработчику и хозяину предмета творчески раскрыть его структуру увидеть оптимальное распределение ресурсов, обеспечивающих жизненный цикл каждого элемента, представить зависимость величины потенциала предмета от отклонений от указанного оптимального распределения ресурсов (см. рис. 2).
Таким образом, тектологическая функция отличается:
1. Возможностью так раскрыть структуру потенциала предмета различной природы и сложности, что все потенциалы ее элементов окажутся связаны конкретной математической зависимостью, что позволяет по критерию качество/цена продукта минимизировать расход обеспечивающих его жизненный цикл средств [1]. Среди указанных предметов и их элементов могут оказаться такие, как потенциалы эргатической системы управления ведомством страны, работника [2, 3], технических и программных средств предмета, формы и содержания предмета, реактивного двигателя и его конкретной шестеренки или болта, авианосца, танка и так далее и т.п.
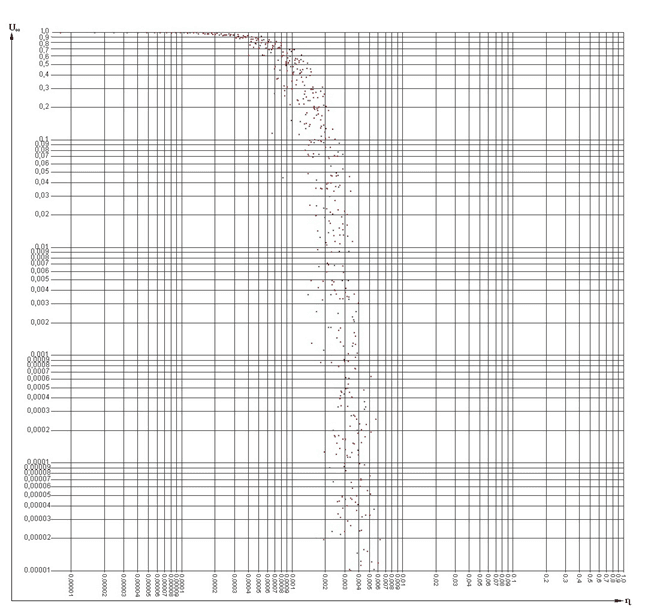
Рис. 2. Зависимость потенциала строения (порядка 10000 nу.к.) от отклонений ƞ (по нормальному закону распределения) от оптимального распределения между элементами предмета ресурсов, обеспечивающих его жизненный цикл
2. Определением сути потенциала формы предмета, которая представляет собой произведение потенциалов (коэффициентов) взаимозависимости fj всех пар потенциалов элементов содержания предмета или выражение геометрической формы предмета однородного содержания [4]. Имеют место случаи, когда элементы содержания предмета ошибочно относят к форме предмета.
3. Способностью вносить вклад в выявление сути единства мира, в тектологию, поскольку позволяет использовать единый способ вычисления потенциалов предметов различной природы и сложности, единый способ раскрытия их структур.
4. Возможностью определить оптимальное (по критерию качество/цена) распределение ресурсов, обеспечивающих жизненный цикл предмета различной природы и сложности, между всеми элементами этого предмета, а также найти зависимость величины потенциала предмета от отклонений от оптимального распределения указанных ресурсов.
5. Уточнением теории исследования операций, одним из основных требований которой является «равнопрочность» по отношению к различным разрушающим факторам случайного или преднамеренного характера. Использование приведенных правил раскрытия структуры потенциала предмета помогает избежать ошибок в обеспечении упомянутой равнопрочности – равнопрочности элементов структуры предмета, завершающих, а не начинающих ее раскрытие.
6. Возможностью более точного определения зависимости между ресурсами и выпуском продукции по сравнению с производственной функцией Кобба-Дугласа (Q = А ٠ Lα ٠ Kβ). В отличии от производственных функций, рассматриваемых экономической наукой, правила тектологической функции позволяют [5] при анализе как действующей, так и перспективной системы производства уйти от использования субъективно назначаемых величин константы А, коэффициента эластичности по труду – α и коэффициента эластичности по капиталу – β. Эти величины появились, чтобы учесть уже сложившиеся на момент анализа системы ее структуру и имеющее место распределение ресурсов между ее специфическими элементами, отклонения от оптимального распределения ресурсов в ней.
При создании и оптимизации расхода ресурсов, обеспечивающих жизненные циклы широко распространенных в мире всевозможных боевых сил и сил производства, требуется иметь профессионально раскрытую структуру потенциала человека [2, 3], потенциалы всех элементов которой желательно устремить к оптимальным величинам.
Обращаюсь к специалистам медицины и психологии с просьбой принять участие в создании структуры потенциала человека, раскрытой по правилам тектологической функции, которая могла бы стать основой для построения на ее основе структур потенциалов работников самых разных специальностей.

.png&w=640&q=75)