Вопрос о минимизации функционалов, связанных с оценками решений дифференциального уравнения с запаздывающим аргументом
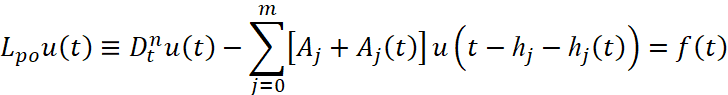
с неограниченными операторными коэффициентами 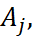
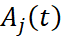 рассмотрен в [1]. В данной работе аналогичный вопрос исследуется для случая уравнения с распределенным запаздыванием
рассмотрен в [1]. В данной работе аналогичный вопрос исследуется для случая уравнения с распределенным запаздыванием
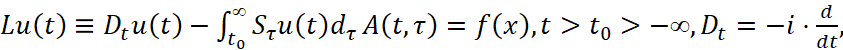 (1)
(1)
где A(t,s) : Y→Y – замкнутая неограниченная оператор-функция, A(t,s): X→Y – ограниченная оператор-функция, X⊂Y, X,Y – гильбертовы пространства, 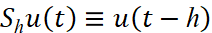 .
.
Полагая существование 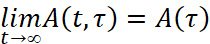 наряду с уравнением (1), будем рассматривать и уравнение
наряду с уравнением (1), будем рассматривать и уравнение
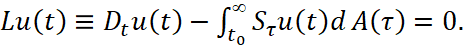 (2)
(2)
Легко видеть, что
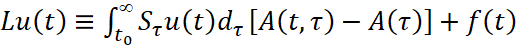 . (3)
. (3)
Определим оператор
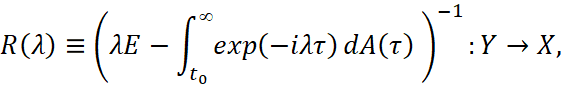
называемый резольвентным оператором для 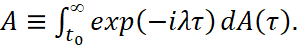 Через ϕ0∈X, ϕ0≠0 обозначим собственный элемент оператора A, соответствующий собственному значению λ0, а через ϕ1,ϕ2,...,ϕn-1∈X – присоединенные к нему, что означает выполнение равенств [2]
Через ϕ0∈X, ϕ0≠0 обозначим собственный элемент оператора A, соответствующий собственному значению λ0, а через ϕ1,ϕ2,...,ϕn-1∈X – присоединенные к нему, что означает выполнение равенств [2]
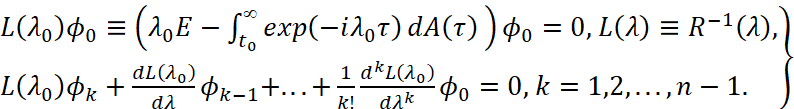 (4)
(4)
В дальнейшем через 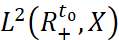 обозначим пространство функций u(t)∈X с нормой
обозначим пространство функций u(t)∈X с нормой 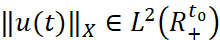 ,
, 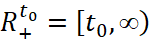 .
.
Лемма 1. Если 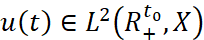 ,
, 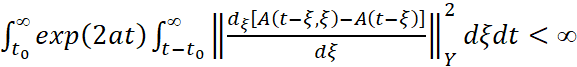 , то функция
, то функция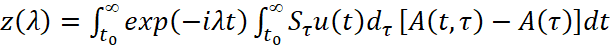 регулярна в полуплоскости
регулярна в полуплоскости 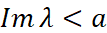 .
.
Доказательство. Непосредственно оценивая норму производной z'(λ), имеем
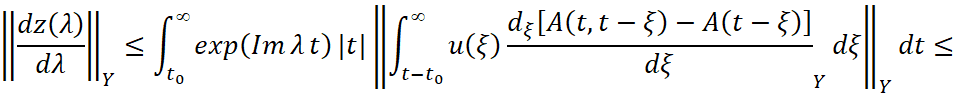
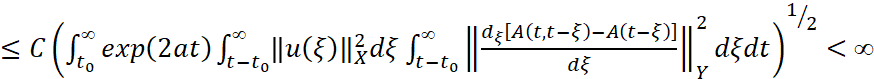 .
.
Лемма доказана.
Лемма 2. Если λ0 – n-кратный полюс резольвенты R(λ), то функция
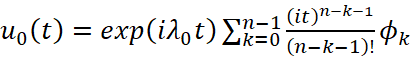 ,
,
где ϕ0 – собственный элемент оператора A, соответствующий собственному значению λ0, а ϕ1,ϕ2,...,ϕn-1 – присоединенные к ϕ0, является решением уравнения (2).
Доказательство. Подставляя u0(t) в (2) и затем, собирая члены при одинаковых степенях t, получим
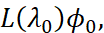
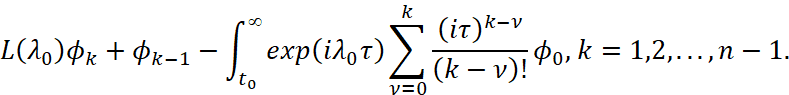
Таким образом,
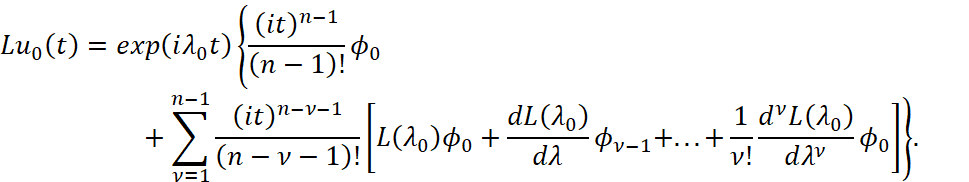
Отсюда и из определения элементов ϕ0,ϕ1,ϕ2,...,ϕn-1, связанных соотношениями (4), следует утверждение леммы.
Лемма 3. Если R(λ) мероморфна в полосе 0<Imλ<a, F(λ) – регулярная в этой полосе функция, то вычеты функции 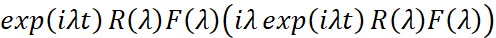 относительно полюсов R(λ) в этой полосе являются решениями (производными от решений) уравнения (2).
относительно полюсов R(λ) в этой полосе являются решениями (производными от решений) уравнения (2).
Доказательство. Если контур γ окружает n-кратный полюс λ0 резольвенты R(λ), то 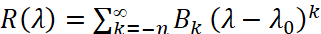 ,
, 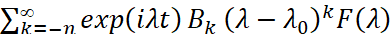 на γ равномерно сходится к функции
на γ равномерно сходится к функции 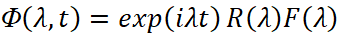 ,
,
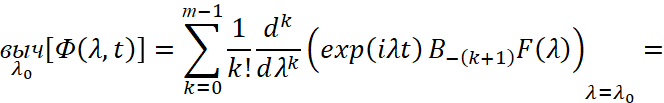
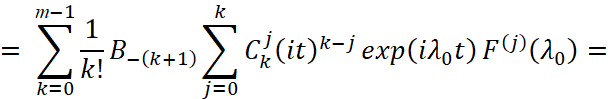
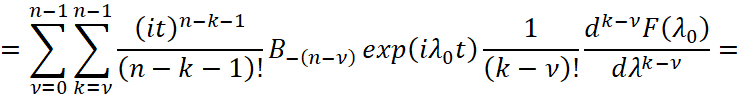
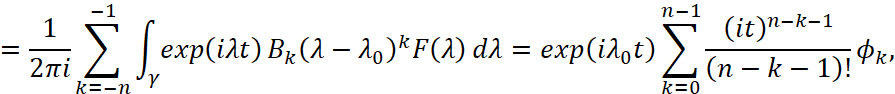
где 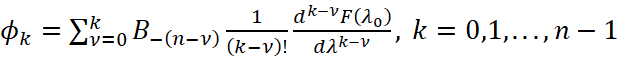 .
.
Нетрудно показать, что ϕk удовлетворяет соотношениям (4).
Доказательство леммы в случае 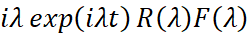 проводится аналогично.
проводится аналогично.
Теорема 1. Пусть выполнены условия:
а) u(t) – решение уравнения (1), 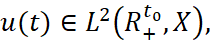
б) R(λ) мероморфна, 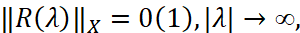
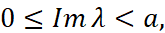
в) 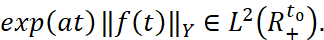
Тогда ∀ε>0 имеется конечное число решений вида 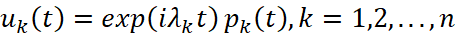 , уравнения (2), где λk - полюс резольвенты R(λ),
, уравнения (2), где λk - полюс резольвенты R(λ), 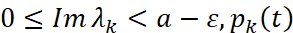 – многочлен, степень которого на единицу меньше кратности полюса λk, что имеет место
– многочлен, степень которого на единицу меньше кратности полюса λk, что имеет место
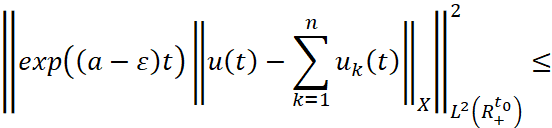
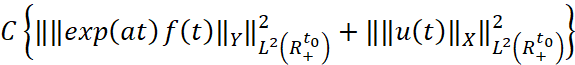 , (5)
, (5)
где постоянная C зависит от a и не зависит от решения u(t).
Доказательство. Рассмотрим функцию η(t)∈C∞, η(t)=0, t≤t0, η(t)=1, t≥t0+1, 0≤η(t)≤1. Тогда для ϑ(t)=η(t)u(t) имеем
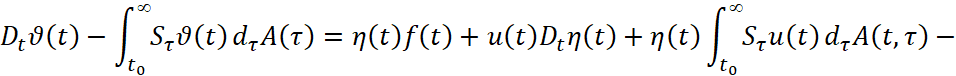
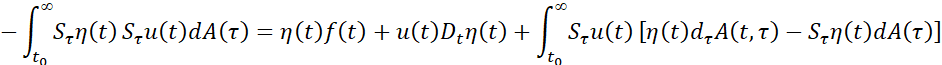
и затем, применив преобразование Фурье, получим
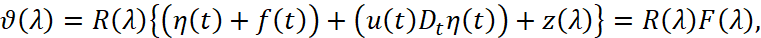 (6)
(6)
где 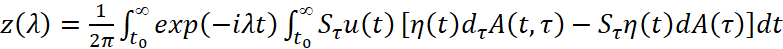 .
.
Так как η(t)=0, t≤t0, то в силу условия в) теоремы и леммы 1 функция z(λ) регулярна в полуплоскости Imλ<a. Функция 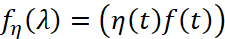 регулярна для Imλ<a в силу условия в) теоремы. Что касается функции (u(t)Dtη(t)), то она является целой функцией экспоненциального типа как преобразование Фурье финитной функции u(t)Dtη(t) в силу хорошо известной теоремы Пели-Винера.
регулярна для Imλ<a в силу условия в) теоремы. Что касается функции (u(t)Dtη(t)), то она является целой функцией экспоненциального типа как преобразование Фурье финитной функции u(t)Dtη(t) в силу хорошо известной теоремы Пели-Винера.
Таким образом, F(λ) регулярна в полосе 0<Imλ<a, а потому полюса ϑ(λ) и R(λ) в этой полосе совпадают. Пусть ε>0 и δ>0 таковы, что a-ε<δ<a и в полосе 0≤Imλ≤a-ε, 0≤Imλ≤δ резольвента R(λ) имеет одинаковое число полюсов. Теперь докажем, что 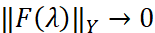 равномерно в полосе 0≤Imλ≤δ при |λ|→∞. Для первых двух слагаемых в фигурных скобках в правой части равенства (5) это очевидно. Что касается функции z(λ), то имеем
равномерно в полосе 0≤Imλ≤δ при |λ|→∞. Для первых двух слагаемых в фигурных скобках в правой части равенства (5) это очевидно. Что касается функции z(λ), то имеем
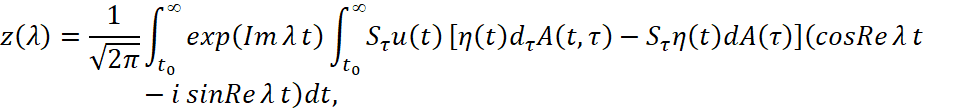
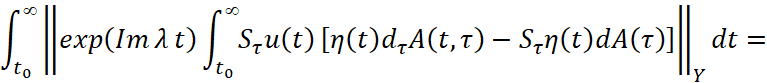
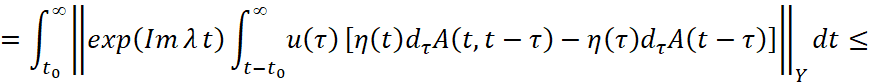
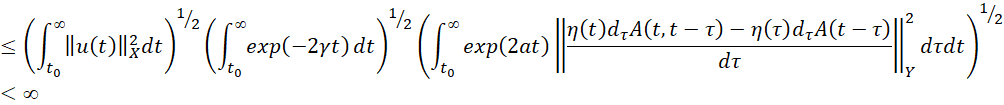
в силу условий а), г) теоремы, где γ>0, 0≤Imλ<a, Imλ+γ<a.
Теперь из теоремы Римана-Лебега следует равномерное стремление к нулю 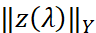 при
при 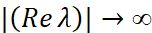 в полосе 0≤Imλ≤δ и
в полосе 0≤Imλ≤δ и 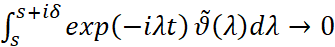 при s→∞. В силу условия а) теоремы и теоремы Планшереля ([1], с. 358) ϑ(λ) не имеет полюсов на Imλ=0. Теперь по теореме Коши о вычетах будем иметь
при s→∞. В силу условия а) теоремы и теоремы Планшереля ([1], с. 358) ϑ(λ) не имеет полюсов на Imλ=0. Теперь по теореме Коши о вычетах будем иметь
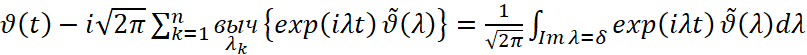 .
.
Применяя леммы 2), 3) и теорему Планшереля из последнего равенства имеем
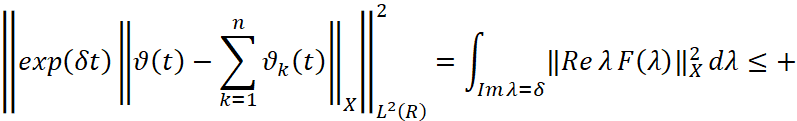
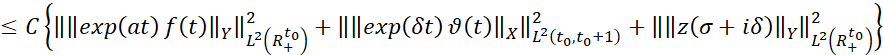 .
.
Оценивая последнюю норму, имеем
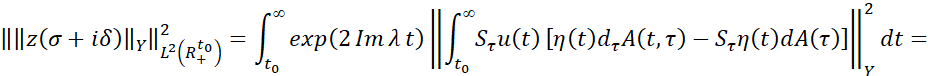
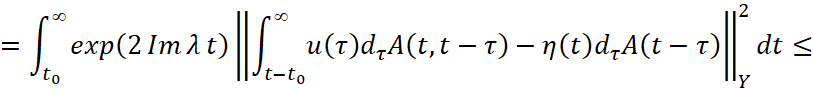
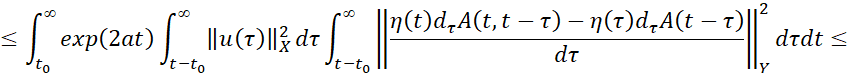
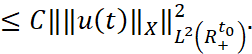
Теорема доказана.
Замечание 1. Если в условиях а), б) теоремы 1 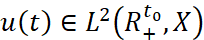 и
и 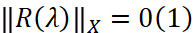 заменить на
заменить на 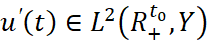 и
и 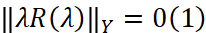 соответственно, то можно получить аналогично оценке (5) асимптотическую оценку для производной u'(t) решения u(t) в виде
соответственно, то можно получить аналогично оценке (5) асимптотическую оценку для производной u'(t) решения u(t) в виде
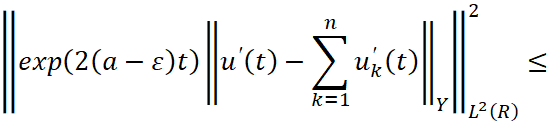
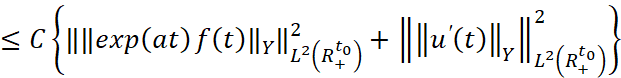 . (7)
. (7)
Теперь рассмотрим функционалы
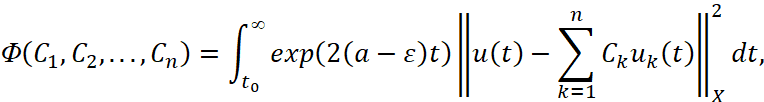
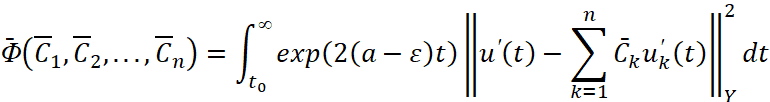
как функции от коэффициентов 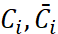 ,
, 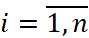 и поставим задачу их минимизации по этим коэффициентам. Очевидно, что это равносильно задаче минимизации функций.
и поставим задачу их минимизации по этим коэффициентам. Очевидно, что это равносильно задаче минимизации функций.
Рассматривая первую из них, имеем
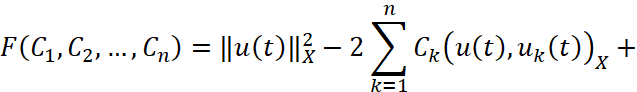
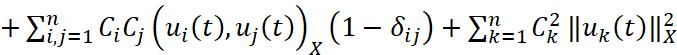 ,
,
δij – символ Кронекера. Далее, приравнивая к нулю первые производные
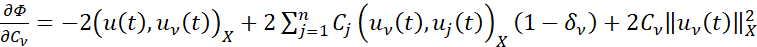 ,
,
получим систему
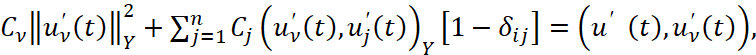
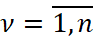 .
.
Дальнейшее доказательство аналогично доказательству теоремы 2.3.1 [1] для случая 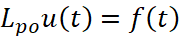 .
.
Замечание 2. Если в формулировке теоремы добавить условие 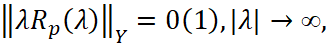 0≤Imλ<a, то оценку (5)
0≤Imλ<a, то оценку (5) 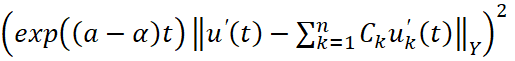 .
.

.png&w=640&q=75)