Гидродинамика движения частиц распыленного материала и сушильного агента

Гидродинамика распылительных аппаратов

Согласно существующей классификации [1-5] аппараты, в которых проводятся непрерывные процессы делятся на:

– Аппараты идеального вытеснения.

– Аппараты идеального перемешивания.

– Аппараты промежуточного типа.

Так как для аппаратов промежуточного типа теоретическое определение движущей силы процесса невозможно, то в этих случаях необходимо проведение специальных экспериментальных исследований.

При разработке математической модели [2] делают обоснованное допущение о гидродинамической модели перемешивания по газовой фазе – идеальное вытеснение.

Трудности, связанные с аналитическим описанием действительной картины движения потоков газа в камере, являются причиной идеализации математических моделей распылительной сушки материалов. Практически для одних аппаратов применяется модель идеального перемешивания, для больших промышленных аппаратов с большой величиной 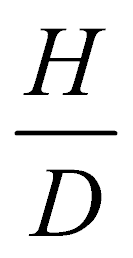 – модель идеального вытеснения [2].

Существуют три основных подхода к построению методик расчета процесса распылительной сушки материалов:

– эмпирические методы расчета;

– аналитические методики расчета;

– комбинированный способ (включает в себя эмпирико-аналитические зависимости).

Применительно к расчету распылительных аппаратов методики, основанные на решении общих дифференциальных уравнений движения продукта и тепло- массообмена, перспективны.

В условиях нисходящего газового потока уравнение равновесия вышеперечисленных сил записывается в виде

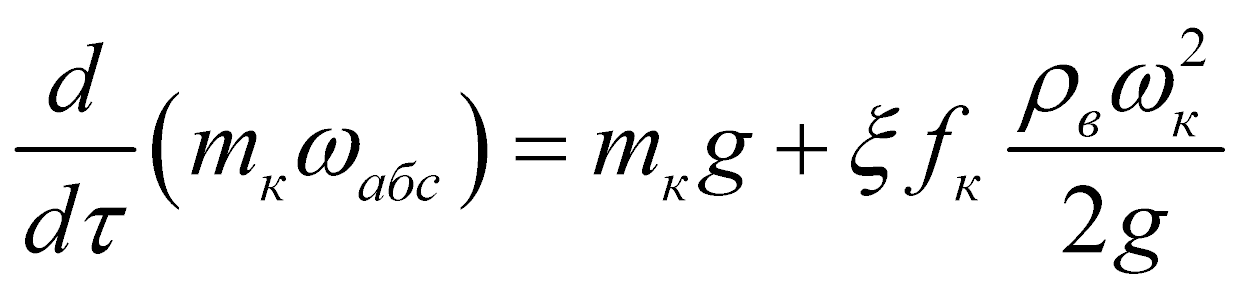 ,                                      (1)

где w_абс, w_к – соответственно абсолютная и относительная скорости частицы; t – время движения частицы; f_к – лобовая поверхность сопротивления капли; x – коэффициент сопротивления; r_в – плотность воздуха.

Применение решений в разрабатываемой инженерной методике расчета только для бесконечно малого участка по высоте сушильной камеры.

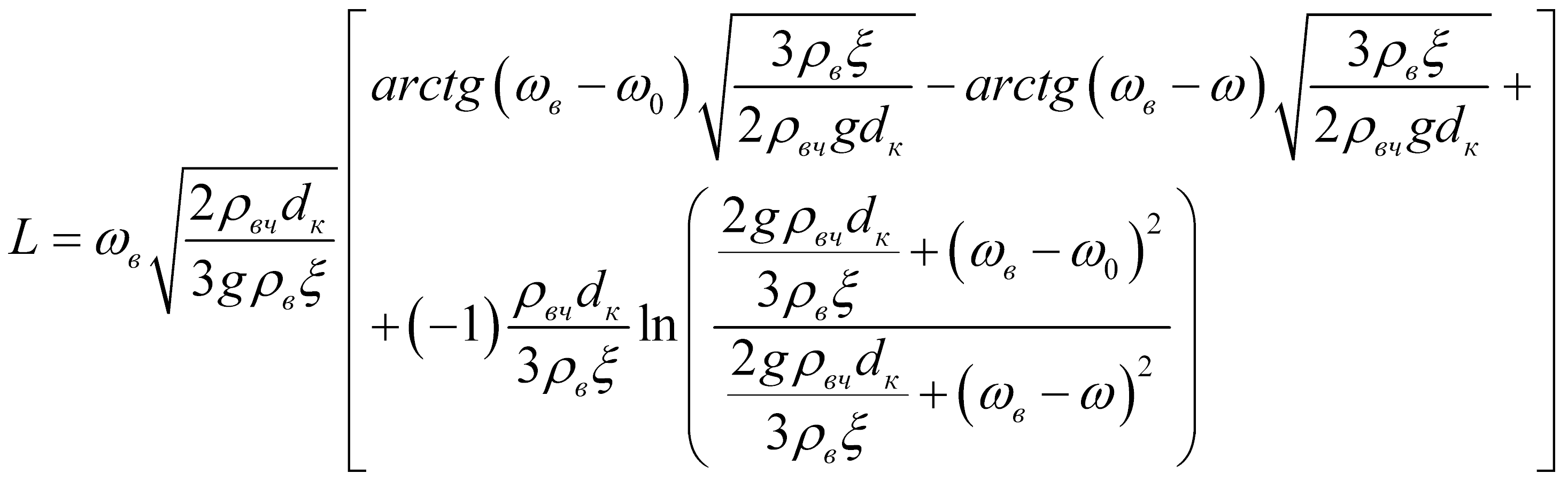, (2)

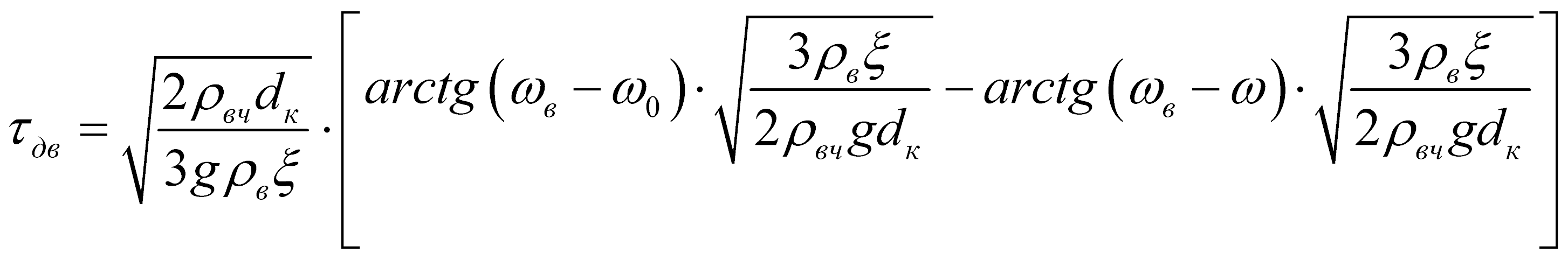, (3)

где L – длина канала по которому движется частица (в нашем случае – высота некоторого сечения по высоте камеры, где можно принять, что масса и диаметр частицы остаются условно постоянными); t_дв – время движения частицы за которое частица пройдет путь L (скорость частицы изменится от w₀ до w), d_k – диаметр капли.

В приведенных выше зависимостях коэффициент сопротивления вычисляется по формуле [2]

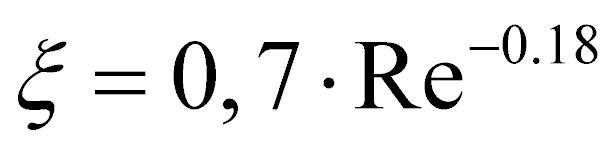.   (4)

Однако, зависимость (4) не учитывает стесненный характер движения частицы. Введение поправки по уравнению (5), предложенному в [6] позволяет вычислить коэффициент сопротивления при движении частиц в реальном потоке

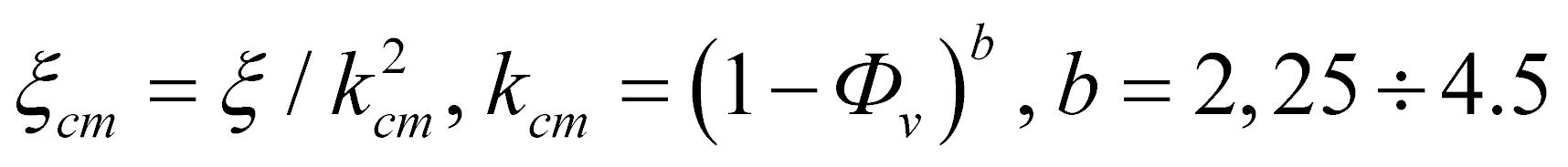,    (5)

где Ф_v – объемная концентрация двухфазного потока, м³/м³.

В уравнениях (2)-(3) скорость влажного двухфазного потока определяется как

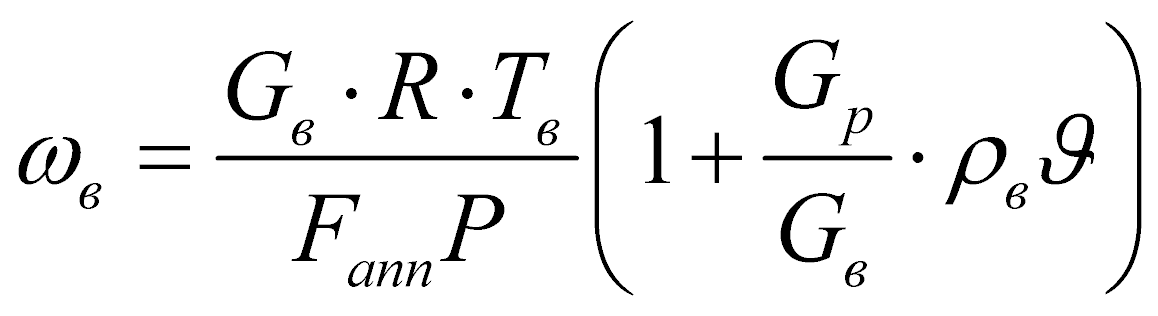,   (6)

где 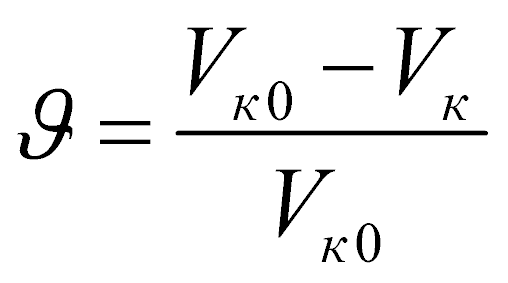 – доля испарившейся жидкости к моменту времени t; F_апп – площадь поперечного сечения сушильной камеры, F_апп = 0,785 D_апп².

Наиболее обоснованным является расчет диаметра камеры исходя из горизонтальных размеров факела распыла [3-5].

Для определения радиуса факела распыла при подаче суспензий красителей на сушку при помощи центробежных дисковых распылителей получена зависимость

,          (7)

где w_д – окружная скорость диска; для производительности по исходной суспензии 400-1000 л/ч составляющие уравнения (7) принимают следующие значения А=1,7; В=4,5; Q₀=400 л/ч; для расчета константы С используются следующие выражения

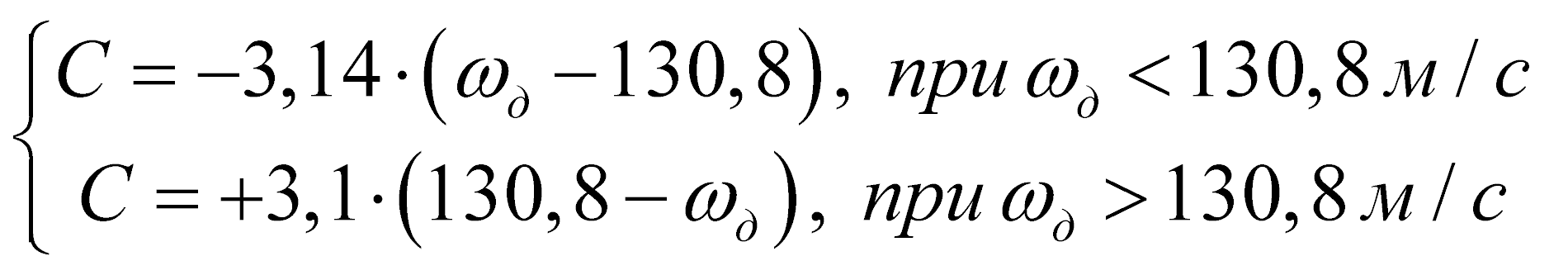. (8)

Выводы

Предложенные уравнения, позволяют определить один из основных геометрических размеров распылительной сушилки – ее диаметр. В зависимости от производительности распыливающего диска.