Подходы к автоматизации алгоритмов анализа и синтеза звена мультисервисной сети связи

В исследуемой системе распределения информации рассматривается процесс совместного использования канального ресурса звена мультисервисной сети связи (МСС) с произвольным числом пуассоновских потоков вызовов (заявок), различающихся интенсивностью поступления, количеством ресурса, выделяемого для обслуживания одной заявки, и временем его занятия на передачу информации пользователя. Несмотря на большую размерность исходных данных для мультисервисной модели обслуживания заявок удалось получить все основные результаты, аналогичные тем, что были ранее сформулированы для классической модели Эрланга и которые способствовали ее широкому применению в деятельности специалистов, занимающихся проектированием сетей связи [1–3]. Для моделей МСС схема занятия канального ресурса зависит от типа поступившей заявки. В данных моделях однородные события, описывающие последовательность моментов поступления заявок сервисов (услуг), требующих для обслуживания разный ресурс линии, приводят к необходимости учета нескольких потоков неординарных вызовов. При этом процессы обслуживания заявок каждого типа должны рассматриваться отдельно. Таким образом, в теории телетрафика мультисервисных систем возникает класс так называемых многопотоковых моделей [2, 3].

Пусть в мультисервисную систему обслуживания (рис. 1) поступает n потоков заявок сервисов реального времени (речевые сообщения, аудиоконференцсвязь, видеоконференцсвязь и др.). Каждый поток требований на обслуживание описывается моделью простейшего потока. Это означает следующее:

• поступление заявок k-го потока (k=1, 2, ..., n) подчиняется закону Пуассона. Интенсивность поступления заявок k-го потока обозначим через λ_k;
• число источников (N_k), формирующих каждый поток нагрузки, не ограничен (N_k > 300–500).

Для предоставления каждого запрашиваемого сервиса требуется b_k  единиц канального ресурса (ЕКР) линии, при этом время занятия ресурса на обслуживание заявки имеет экспоненциальное распределение с параметром μ_k, k=1, 2, 3, ..., n.  В этом случае поступающая нагрузка от k-го потока будет равна Z_k=λ_k/μ_k.

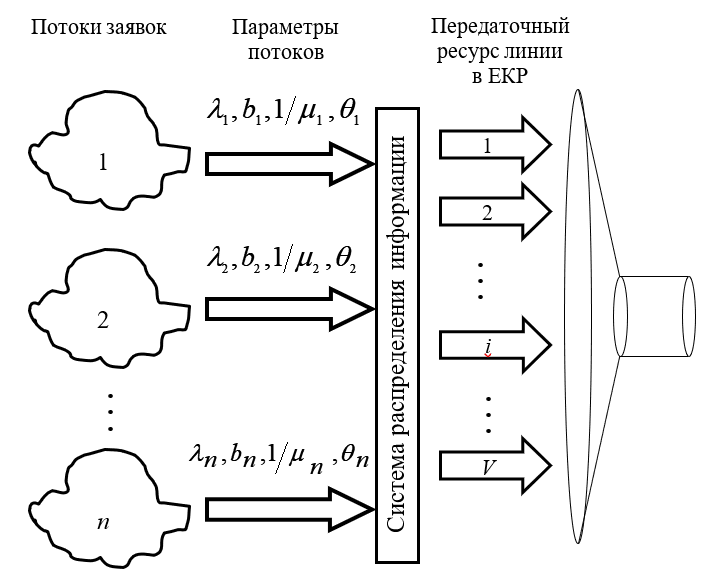
Рис. 1. Модель мультисервисной системы обслуживания

Схема коммутации – полнодоступная. При этом величина V обозначает скорость передачи информации мультисервисной линии, выраженную в ЕКР.

Для доступа к передаточному ресурсу линии используется стратегия доступа с резервированием каналов (TR – Trunk Reservation). Данная стратегия предусматривает для каждого k-го потока введение индивидуального порога резервирования канального ресурса (РКР) – θ_k  (θ_k≤V). Обозначим через i  общее число занятых канальных единиц в момент поступления заявки. Если выполняется неравенство i>θ_k, то поступившая заявка k-го потока считается потерянной и не возобновляется. В противном случае заявка принимается к обслуживанию.

Число ЕКР линии, необходимое для обслуживания одной заявки k-го потока, обозначим символом b_k. Величины V и b_k – целые положительные числа.

Дисциплина обслуживания заявок – с явными потерями, т. е. в случае нехватки необходимого объема канального ресурса (скорости, выраженной в ЕКР) заявки получают отказ и повторно для обслуживания в систему не поступают.

Требуется при заданных параметрах входных потоков (n,λ_k,b_k,μ_k), структуры (V) и дисциплины обслуживания (θ_k) МСС определить вероятность потерь заявок (π_k) и долю обслуженной нагрузки (Y_k) для каждого k-го сервиса (k=1, 2, 3, ..., n.). В теории телетрафика такая задача классифицируется как задача анализа. Решение обратной задачи (задачи синтеза) сводится к нахождению необходимого объема канального ресурса (V) звена МСС при заданных параметрах потоков (n,λ_k,b_k,μ_k ), дисциплине обслуживания (θ_k) и нормах на потери заявок (π_k ≤ π*).

Для решения сформулированных задач разработано несколько алгоритмов, программно реализованных в среде программирования C++. Для снижения вычислительной сложности применяется метод Кауфмана-Робертса, основанный на разбиении пространства состояний модели по числу занятых ЕКР [2]. Построенные на основе данного метода алгоритмы относятся к классу "рекурсивных" с полиномиальной вычислительной сложностью [3]. В данном случае под рекурсией понимается процедура определения вероятностей потерь через предыдущие состояния системы, которая при решении задачи анализа МСС сводится к выполнению последовательности следующих основных шагов:

1. Задать исходные данные:

• n – число категорий услуг (речь, видеосвязь, ВКС и др.);
• Z_k – интенсивность нагрузки, поступающей от k-категории пользователей (k=1, 2, ..., n);
• b_k – канальный ресурс, необходимый для обслуживания одной заявки k-го потока (категории);
• V – скорость передачи информации мультисервисной линии, выраженная в ЕКР.
• θ_k – индивидуальный порог резервирования канального ресурса (θ_k≤V).

2. Присвоить значение "1":

P(0)=1.

3. Через P(0), последовательно увеличивая i от 1 до V (i=1,2,...,V), вычислить значения ненормированных вероятностей P(i)  из соотношения 

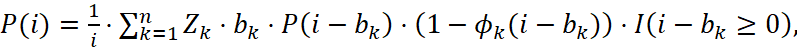    (1)

где I(⋅) – индикаторная функция, определяемая соотношением

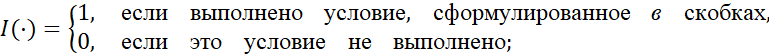
ϕ_k(i) – функция внутренней блокировки вычисляется по формуле

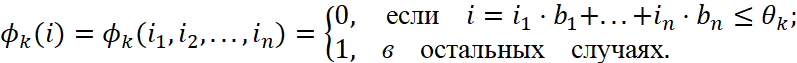
4. Рассчитать значение нормировочной константы

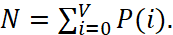     (2)

5. Определить нормированные значения вероятностей p(i) через ненормированные P(i)

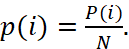    (3)

6. Найти значения показателей качества совместного обслуживания заявок для каждого k-го потока

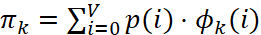;    (4)

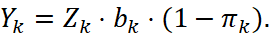    (5)

Задача синтеза решается на основе многократного использования алгоритма анализа, предполагает выполнение следующей последовательности шагов (рис. 2):

1. Задать исходные данные: n, b_k, z_k, θ_k, V_нач. Как правило, начальное значение канального ресурса звена V_нач выбирается равным интенсивности поступающего трафика в ЕКР.
2. Задать нормированные значения вероятности потерь π_k из соответствующих руководящих документов, регламентирующих требования к качеству обслуживания (QoS) заявок различных сервисов в МСС.

Здесь следует отметить, что работы по стандартизации качества обслуживания на уровне управления соединениями (сеанса связи) для МСС не завершены. Кроме того, в звене МСС обслуживаются несколько типов потоков трафика (речь, видео и т. д.), каждый из которых может существенно различаться требованиями к потерям и объему необходимого сетевого канального ресурса. Поэтому при нормировании значений вероятностей потерь в качестве общего функционала, как правило, берут максимальное значение доли потерянных заявок π, определяемое как

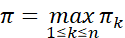    (6)

При условии π₁<π₂<,...,<π_k  данный функционал будет равен π_k.

Другой подход при решении задачи синтеза заключается в использовании значения π_l, определяемого как отношение доли обслуженного трафика к величине предложенного трафика из функционала

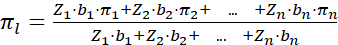.     (7)

3. Принять расчетное V равным начальному значению величины канального ресурса V_нач.

4. Рассчитать значения вероятности потерь π_k (либо π_l) с использованием рекурсивного алгоритма (1)–(5).

5. Сравнить рассчитанное значение вероятности потерь с нормированной величиной. При этом предполагается, что значение вероятности потерь (6) или (7) убывает с увеличением числа ЕКР (V) при фиксированных значениях параметров потоков. Если потери выше нормы, то его объём увеличивается, и расчеты повторяются. Если равна или меньше, то задача синтеза решена. Улучшение полученного решения может достигаться за счет применения оптимальной для рассматриваемых условий стратегии доступа и варьированием значений управляемых параметров (например, порогами РКР θ_k) в области допустимых значений [5].

Таким образом, предложенные алгоритмические конструкции, доведенные до программной реализации, являются достаточно универсальными, позволяют решать широкий перечень задач анализа и синтеза МСС. При соответствующем выборе нагрузочных и структурных параметров может быть исследован процесс обслуживания заявок при различных стратегиях доступа к канальному ресурсу звена МСС. Так, например, при θ_k=V имеем полнодоступную стратегию, при θ_k<V – с РКС, при Vk=const – с кластеризацией (V₁ + V₂ +… + V_n = V). Кроме того, используя вместо формул (1) и (4), (5) выражения, полученные в [4], получаем возможность учесть приоритетную дисциплину обслуживания. Приняв b_k = 1, расчет сводится к первой формуле Эрланга, которая традиционно используется для моносервисных сетей.

Результаты моделирования в широком диапазоне исходных данных, сопоставимых с реальными условиями функционирования МСС, показали, что такой подход позволяет получить пусть не оптимальное, но всегда приемлемое для практики решение. Пример решения задачи синтеза с использованием рекурсивного алгоритма показан в таблице.

Решение получено для следующих исходных данных: n=2; b₁=1, b₂=2, Z₁=2 Эрл, Z₂=1 Эрл, V_нач = 1. Так как интуитивно можно предположить, что качество обслуживания ресурсоемких требований будет хуже сервисов, требующих для обслуживания всего лишь один канал, то воспользовались формулой (6) и зафиксировали значение π₂≤0,1. Необходимо найти требуемое значение объема канального ресурса для обеспечения заданных норм потерь – V_треб.

Таблица

Результаты моделирования мультисервисного обслуживания одноканальных (b₁=1) и двухканальных заявок (b₂=2)

Как видно, процедура вычисления даже при малой размерности исходных данных является достаточно трудоемкой. Последовательно увеличивая канальный ресурс на одну единицу при каждом прогоне, решение было получено после девяти итераций (табл.): V_треб = 9. С увеличением объема канального ресурса линии (V) и числа категорий трафика (n) растут вычислительная сложность и время расчета, что делает актуальным автоматизацию процедур расчета.

Для автоматизации процедур решения задач анализа и синтеза на основе рассмотренных алгоритмов было разработано специальное программное обеспечение. Вид основных оконных форм программного продукта представлен на рисунке 3, 4.

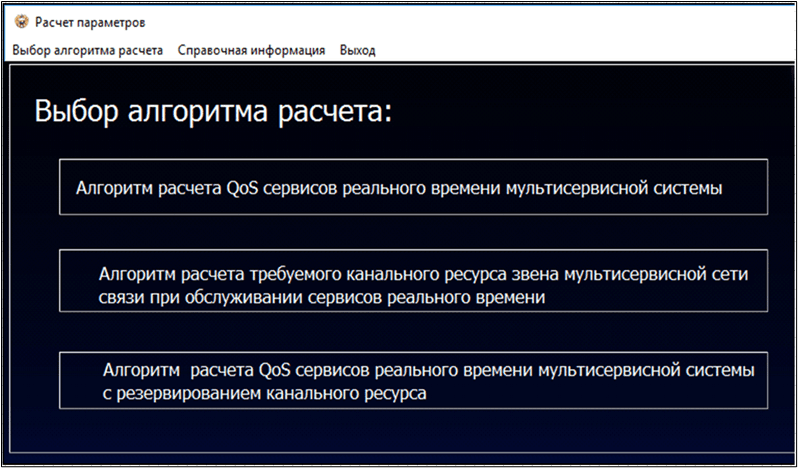
Рис. 3. Окно пользовательского интерфейса при запуске программы и выборе расчетного алгоритма

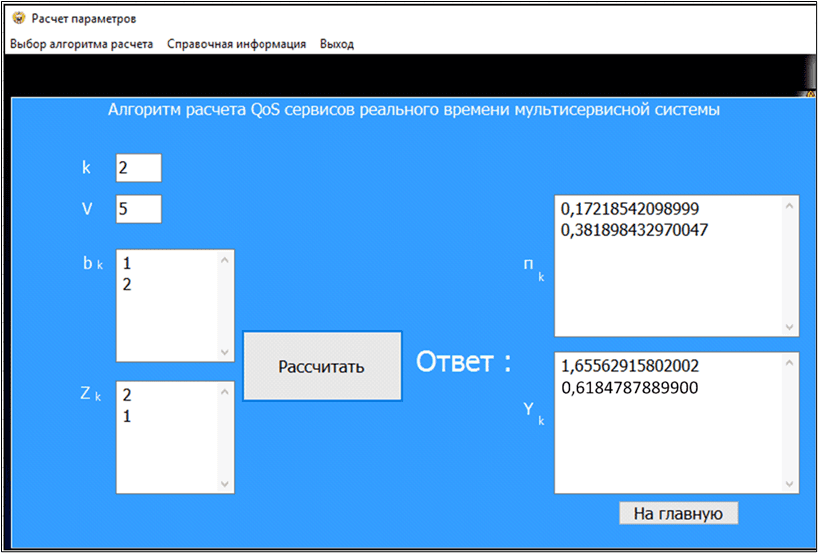
Рис. 4. Окно пользовательского интерфейса для ввода исходных данных. Пример расчета

Выводы

Поведенные исследования показали, что зависимости вероятностей потерь заявок различных сервисов от изменения объема канального ресурса имеет сложный ярко выраженный нелинейный характер. Установлено, что данный эффект усиливается с увеличением количества потоков заявок. Без наличия соответствующего инструментария найти правильное решение по обеспечению требуемого качества обслуживания заявок в условиях мультисервисного трафика и применения различных стратегий доступа к ресурсам проблематично, а при увеличении количества разнотипных потоков – не представляется возможным. В связи с этим задачи, связанные с совершенствованием и автоматизацией алгоритмов анализа и синтеза МСС, являются важными и актуальными. На конкретных примерах расчета для исходных данных, соответствующих условиям функционирования МСС, показана возможность использования разработанных модельно-алгоритмических конструкций для решения широкого перечня научно-практических задач. Созданные на их основе программные продукты могут быть применены в системе поддержки принятия решений по обеспечению требуемого качества обслуживания на этапах проектирования и эксплуатации МСС.