В настоящее время наиболее распространенным типом перекрытий в массовом строительстве являются плоские безбалочные перекрытия. Их долговечность и эксплуатационная надёжность зависят как от учёта особенностей используемых материалов [1-3], так и от степени изученности напряжённо-деформированного состояния узла опирания плиты на колонну.
Прочность предлагаемых технологами материалов возрастает [4, 5], это обстоятельство и появление на рынке композитных материалов [6] позволяют уменьшать сечения несущих конструкций. В связи с этим весьма важен вопрос обеспечения надёжности узла сопряжения плиты с колоннами.
Продавливание плиты происходит, когда усилие от внешней нагрузки, приходящее в узел сопряжения, превышает предельное усилие, которое может воспринять бетон и поперечная арматура. Фактическая форма поверхности, по которой происходит разрушение плиты, имеет сложный вид и зависит от многих факторов [7-9]. Изучению этого вопроса посвящено большое количество работ, но пока нет единого мнения о работе плиты при продавливании и механизме разрушения [9, 10].
Расчётные предпосылки и расчётные модели, используемые в нашей стране и за рубежом, отличаются. Если взять только нашу страну – в разное время подход к расчёту на продавливание менялся.
Согласно действующему нормативному документу Российской Федерации СП 63.13330.2018 «Бетонные и железобетонные конструкции. Основные положения» условие прочности при действии только продольной силы и отсутствии поперечной арматуры имеет вид:
F ≤ Fb,ult (1)
где F – сосредоточенная сила от внешней нагрузки;
Fb,ult – предельное усилие, воспринимаемое бетоном, которое равно:
Fb,ult = Rbt·Ab (2)
где Аb – площадь расчетного поперечного сечения, расположенного на расстоянии ho/2 от границы площади приложения сосредоточенной силы F, определяемая по формуле:
Аb = u·ho
В этой формуле:
u – периметр контура расчетного поперечного сечения,
ho - приведенная рабочая высота сечения.
Очевидно, что, предельное усилие, воспринимаемое бетоном, равно:
Fb,ult = Rbt·[ 2(a+b+2ho)]· ho,
где а и b – размеры сторон колонны.
В программном комплексе Лира-САПР был выполнен вычислительный эксперимент. В качестве расчётной модели был принят 16-ти этажный каркас жилого дома с безбалочными плитами перекрытий. Рассматривалось продавливание железобетонной плиты на отм. +9.600 квадратным штампом с размерами, равными поперечному сечению колонны 500х500 мм (рис.1). Толщина плиты равна 220 мм, расчетное сопротивление бетона осевому растяжению Rbt = 1,05 МПа.
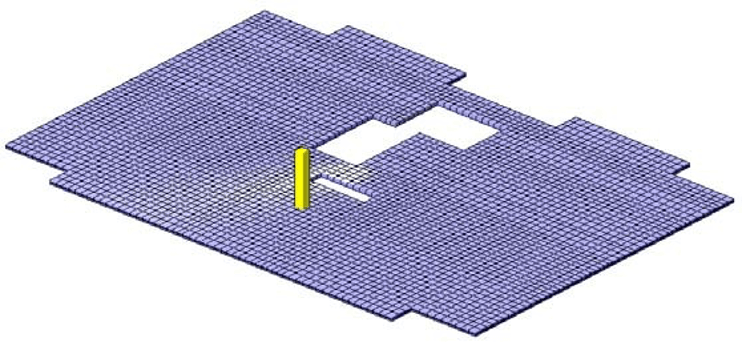
Рис. 1. Конечно-элементная модель плиты
Для квадратного сечения колонны формула упрощается:
Fb,ult = Rbt·[4(a+ho)]· ho.
После подстановки в неё численных значений получим, что бетон в расчетном сечении может воспринять усилие Fb,ult = 565 кН.
Усилие продавливания F = 310,08 кН (из расчёта в ПК Лира-САПР).
В СНиП 2.03.01-84*«Бетонные и железобетонные конструкции» принималось, что продавливание происходит по поверхности пирамиды, меньшим основанием которой служит площадь действия продавливающей силы, а боковые грани наклонены под углом 45°. Расчёт на продавливание плитных конструкций без поперечной арматуры производился из условия:
F≤ Rbt·Um·ho (3)
где Um – среднеарифметическое значение периметров верхнего и нижнего оснований пирамиды продавливания;
Um = 0,5[(2a+2b)+(2(a+2ho)+ 2(b+2ho))] = 2(a+b+2ho) (4)
где ho – рабочая высота плиты.
Использованная расчётная модель в виде пирамиды продавливания была унаследована от более раннего документа – СНиП II-В.12-62.
В действующем СП 63.13330.2018 о пирамиде продавливания не упоминается, а вводится понятие периметра контура расчётного поперечного сечения, расположенного на расстоянии 0,5ho от границы приложения сосредоточенной силы. В соответствии с определением, контур представляет собой прямоугольник или квадрат (в зависимости от сечения колонны) с периметром равным:
u=2(a+2ho/2)+2(b+2ho/2)= 2(a+b+2ho) (5)
Сравнивая выражения (4) и (5), видим, что численные значения предельных усилий, воспринимаемых бетоном при продавливании, вычисленные по формулам (2) и (3), будут совпадать.
Следовательно, поскольку F = 310,08 кН меньше Fb,ult = 565 кН, прочность обеспечена как по старым, так и по новым нормам.
Основным отличием СП 63.13330.2018 от ранних норм является необходимость учёта влияния изгибающих моментов. В расчётной модели принято, что моменты ведут к появлению по периметру расчётного контура касательных напряжений. Считается, что эти напряжения линейно изменяются по длине расчётного контура в направлении действия момента и достигают максимума у противоположных сторон расчётного контура, перпендикулярных плоскости действия момента.
Максимальные изгибающие моменты в плите (рис.2) обусловили выбор узла сопряжения, рассчитываемого на продавливание.

Рис. 2. Мозаика напряжений по Мх
Расчет элементов без поперечной арматуры на продавливание при совместном действии сосредоточенной силы и изгибающего момента производят из условия:
F/Fb,ult + Mx /Mbx,ult + My /Mby,ult ≤ 1 (6)
После подстановки в формулу (6) численные значения, получим:
310,08/565 + 42,4/130,8 + 36,6/130,8 = 1,153 >1
Как видим, в отличие от прежних норм прочность узла не обеспечена – требуется установка поперечной арматуры.
Формула расчета на продавливание по американским нормам ACI 318-14 «Требования строительных норм и правил для железобетона» имеет вид:
ϕVn ≥ Vu,
где Vn – нормативное значение прочности на продавливание,
Vu – фактическое значение нагрузки,
ϕ – коэффициент снижения прочности.
Vn = μ·Avf ·fy, Vu =F/(u·ho) + (v·M)/Wb.
Доля момента, учитываемая в расчете на продавливание, определяется коэффициентом v = 1 – [1/ (1+2/3*√(lx/ly))].
Формула расчета на продавливание по EN 1992 Eurocode 2: «Design of concrete structures. Part 1: General rules and rules for buildings» имеет вид:
VEd ≤ VRd,с,
где VEd – расчетная продавливающая сила,
VRd,с – расчетное значение
сопротивления продавливанию плиты без учета арматуры, которое учитывает продольное армирование плиты перекрытия с помощью эмпирического коэффициента 100 1, где 1 – коэффициент армирования:
VRd,с = СRd,с·k· (100p1·fск) 1/3 + k1·σср ≥ (Vmin + k1·σср),
также в формуле учитывается влияние изгибающего момента:
vEd = β·(VEd /(ui·d)),
β = 1 + k·(MEd/VEd) · (u1/W1),
где β – коэффициент сдвига, принимаемый равным 1,4 (учитывает поправку на передачу момента).
Основное отличие норм EN 1992 Eurocode 2: «Design of concrete structures. Part 1: General rules and rules for buildings» от отечественных и американских норм заключается в назначении расчетного периметра и гипотезе о равномерном распределении скалывающих напряжений по длине сторон расчётного периметра.
Как видим, рассмотренные нормы проектирования учитывают изгибающие моменты либо путём введения в расчётную модель касательных напряжений, действующих по сторонам расчётного контура, либо введением эмпирического коэффициента. Различие наблюдается и в определении самого расчётного периметра, так в Eurocode 2 периметр принимается в виде фигуры, описанной линией, проведенной на расстоянии 2d от загруженного участка (рис.3). Под величиной «d» здесь понимают значение средней расчетной толщины плиты.
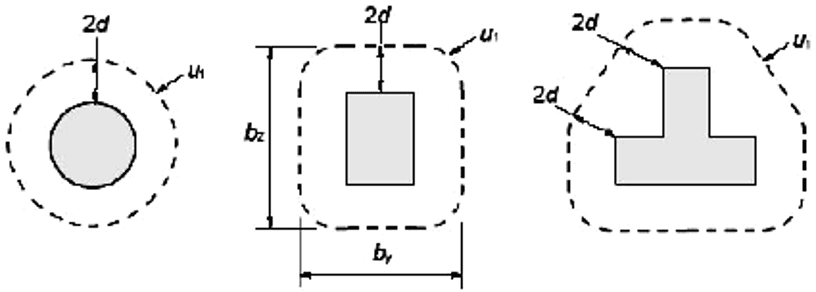
Рис. 3. Критический периметр для площадей приложения местной нагрузки, удаленных от свободных краев плиты и отверстий
Прочность плиты без поперечного армирования на продавливание согласно строительным нормам Белоруссии следует проверять из условия:
VSd ≤ VRd, с = [0,15k·(100p1·fск) 1/3 – 0,10 σср]·d,
но не менее (0,5fctd - 0,10 σср)·d, где VSd – результирующая поперечная сила, действующая по длине критического периметра, который для круговых и прямоугольных в плане площадей приложения местной нагрузки, расположенных на удалении от свободных краев плиты, следует определять как периметр, отстоящий на расстоянии 1,5d от их внешней грани, где d – средняя расчетная толщина плиты.
В нормах РФ рассматривается сечение, которое расположено вокруг зоны передачи усилий на плиту на расстоянии ho/2, где ho – приведенная рабочая высота сечения.
Таким образом, в рассмотренных методиках расчёта на продавливание использованы схожие расчётные модели и учтены одинаковые силовые факторы, как продавливающее усилие, так и изгибающие моменты. Последние учитываются по-разному: либо путём введения в расчётную модель касательных напряжений, либо введением эмпирического коэффициента. Причём форма эпюр касательных напряжений предлагается разная. Не одинаков подход и к назначению геометрических параметров расчётного (критического) контура, при этом разница размеров контуров, полученных по рекомендациям рассмотренных методик, весьма существенна. Очевидно, что работа узла сопряжения безбалочной плиты с колонной изучена пока не в полной мере и требуются дополнительные исследования по обобщению методик расчёта.

.png&w=640&q=75)