Введение
Каждый инструмент обработки сигналов разработан с целью адаптации одного или нескольких сигналов разных классов, однако для всех классов одновременно данный инструмент не имеет возможности достоверной и правдоподобной обработки. Спектральный анализ также зависим от этой проблемы. Применяя различные методы спектрального анализа к классам сигналов можно добиться наилучших результатов. Стоит отметить, что выбор классифицирующих свойств является принципиальным, поскольку само определение классов повлияет на вид инструментов обработки. Традиционно первым классифицирующим свойством является детерминированный или недетерминированный характер сигнала.
Детерминированный сигнал
Существует множество определений детерминизма, однако самым простым является то, в котором математическое воспроизведение непрерывного временного сигнала x(t) (или дискретного x(k)) дает идентичный сигнал [1]. Другое определение, более точно раскрывающее понятие детерминизма, основывается на теории случайных сигналов, при точно прогнозируемом характере x(t) (например, сингулярный член разложения Вольда). В данной статье мы изучим то определение, основой которого является воспроизведение x(t), поскольку это позволит применить известные и легко воспроизводимые алгоритмы обработки сигналов. Следует отметить, что информация о сигнале, содержащаяся в функции, при биективном преобразовании x(t) сохранится. Так же представление сигнала без потери информации, по сравнению с прямым представлением функции x(t), лучше демонстрирует характеристики сигнала.
По интегральным свойствам x(t), детерминированные сигналы принято разделять на классы, которые в свою очередь связаны с некоторыми физическими величинами.
Сигналы с конечной энергией подтверждают интегральные свойства (1) и (2) с непрерывным или дискретным временем.
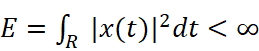 (1)
(1)
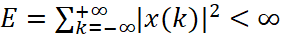 (2)
(2)
Функция x(t) принадлежит к стандартным функциональным пространствам, а интеграл представляет собой энергию сигнала Е.
Сигналы конечной средней мощности представляют, как:
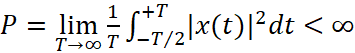 (3)
(3)
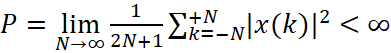 (4)
(4)
Если учесть тот факт, что суммы из уравнений (1) или (2) представляют «энергию», тогда уравнения (3) или (4) представляют мощности.
Ясно, что эти интегральные свойства соответствуют математическим характеристикам, морфологическое поведение которых по оси времени сильно различается: сигналы с конечной энергией будут на практике «импульсными» или «переходными» сигналами такие, что |x(t)|→0 для |t|→∞. Это асимптотическое поведение вовсе не обязательно для обеспечения сходимости сумм, и тем не менее все практические сигналы с конечной энергией подтверждают это. В качестве простого примера приведенный ниже сигнал имеет конечную энергию:
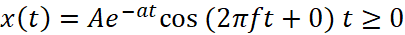
x()t=0 t<0
Затухающий экспоненциальный колебательный сигнал [2] данного типа составляет основу в анализе линейных систем, которые в свою очередь инвариантны относительно переноса.
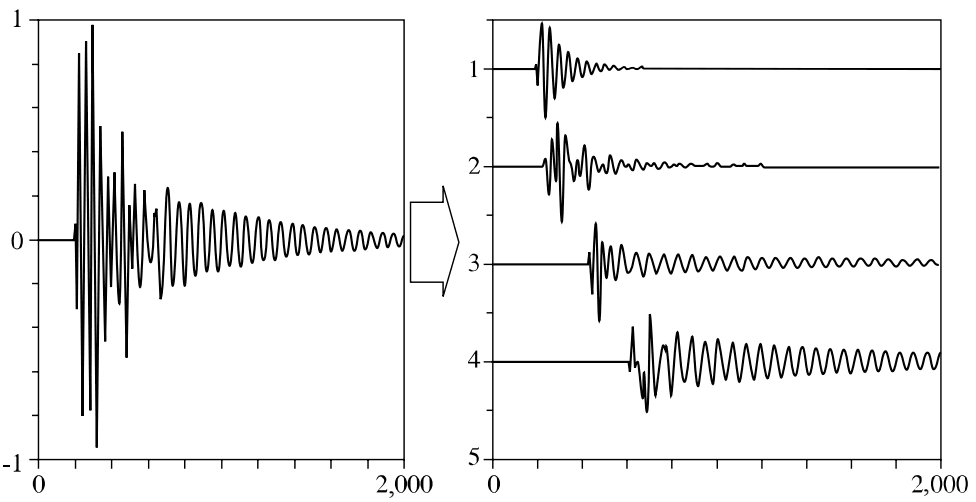
Рис. 1. Сигнал электромагнитной помехи и его разложение
На рисунке 1 отображен сигнал конечной энергии, имеющий следующую форму:
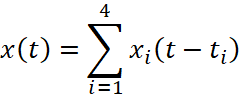
где 4 компонента xi(t) берут свое начало в разные моменты времени {ti}. Комплексная форма сигнала, представленная таким образом, отражает идеально воспроизводимый физический эксперимент [3].
Сигналы, имеющие конечную мощность, на практике являются постоянными сигналами. В качестве примера:
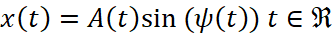 (5)
(5)
|A(t)|<∞
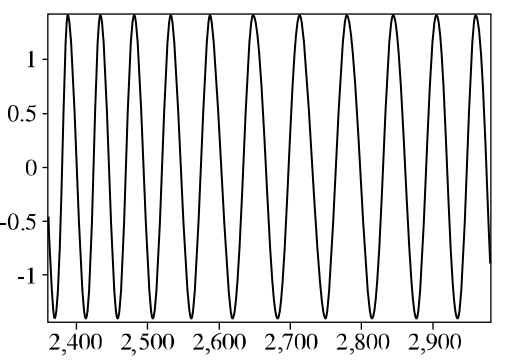
Рис. 2. Частотно модулированная синусоида
Сигнал на рисунке 2 уместно представить уравнением (5). Этот тип сигнала, модулированный по амплитуде и углу, является основным в телекоммуникациях [4].
Вывод
В данной статье были рассмотрены основные математические характеристики детерминированных сигналов. Изучение характеристик сигналов поможет в дальнейшем перейти к изучению основ спектрального анализа.

.png&w=640&q=75)