Рассматривается уравнение
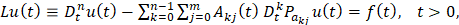 (1)
(1)
с неограниченными линейными операторными коэффициентами
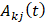 : X→Y
: X→Y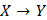 ,
, 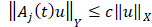 ,
, 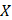 и
и 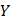 – гильбертовы пространства,
– гильбертовы пространства, 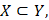
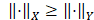 ,
, 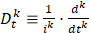 ,
, 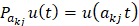 ,
, 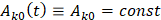 ,
, 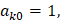
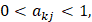
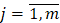 ,
, 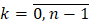 .
.
Оператор 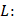
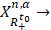
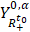 , где пространства
, где пространства 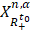 и
и 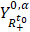 определяются нормами
определяются нормами
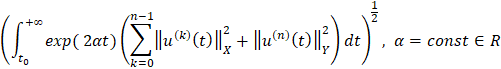
и
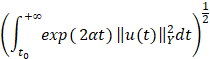
соответственно. Подробные определения см. [1, с.6-12]. Нам также понадобится пространство 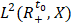 , определяемое нормой
, определяемое нормой
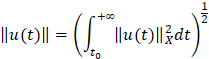
Если уравнение (1) рассматривается на полуоси t>0, то начальное множество 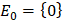 , а начальное условие сводится к
, а начальное условие сводится к 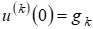 ,
, 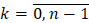 .
.
Уравнение (1) запишем в виде
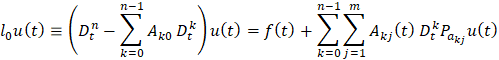 .
.
Тогда для оператора 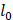 резольвентным оператором будет
резольвентным оператором будет
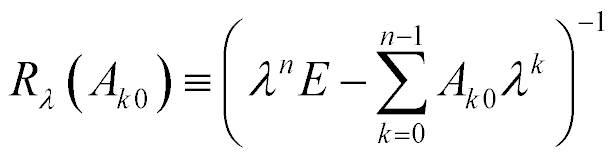
.
Для 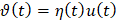 , где
, где
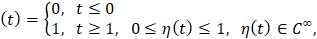
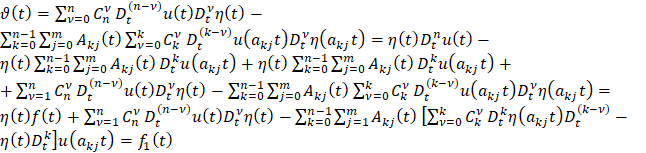 .
.
Отсюда
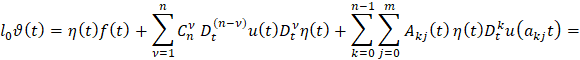
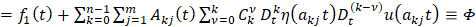 t
t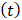 .
.
Применяя к этому уравнению преобразование Фурье, получим
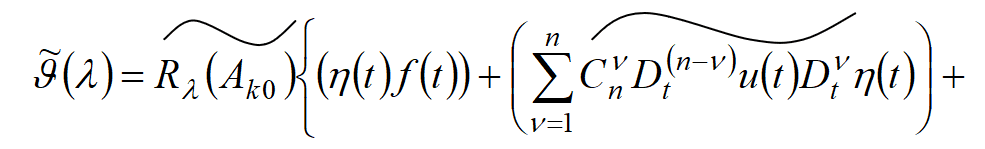
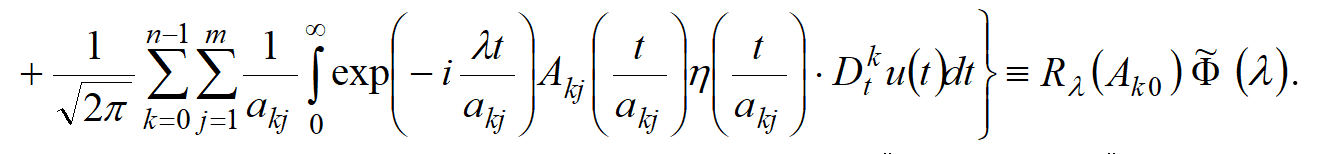
Теорема. Пусть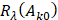 регулярна,
регулярна, 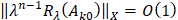 ,
, 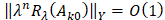 ,
, 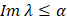 ,
, 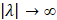 ,
, 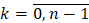 .
.
Тогда существует ε>0 такое, что если 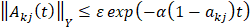 , то оператор
, то оператор 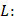
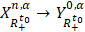 непрерывно обратим.
непрерывно обратим.
Доказательство. Представим уравнение (1) виде
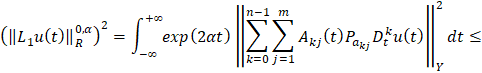
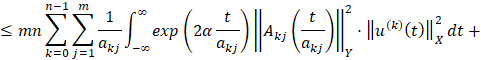
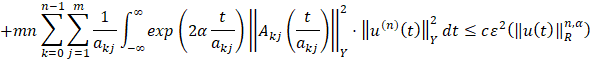 .
.
В силу теоремы 1 [2, с.185], оператор 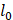 обратим. Тогда по теореме из функционального анализа об обратимости оператора, мало отличающегося от обратимого, из последнего неравенства следует, что оператор
обратим. Тогда по теореме из функционального анализа об обратимости оператора, мало отличающегося от обратимого, из последнего неравенства следует, что оператор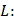
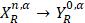 непрерывно обратим, что означает существование единственного решения u(t) уравнения
непрерывно обратим, что означает существование единственного решения u(t) уравнения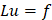 , принадлежащего пространству
, принадлежащего пространству 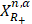 для
для 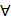
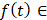
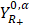 . Остается показать, что
. Остается показать, что 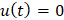 для
для 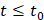 ,
, 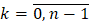 . Для любого
. Для любого 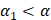 существует единственное решение
существует единственное решение 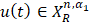 и справедливо неравенство
и справедливо неравенство 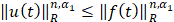 , т.е.
, т.е.
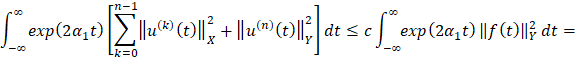
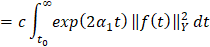 .
.
Отсюда имеем 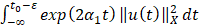
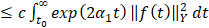 . Умножая обе части полученного неравенства на
. Умножая обе части полученного неравенства на 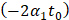 , получим
, получим
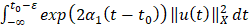
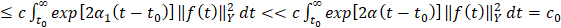 .
.
Так как в силу условий на резольвенту можно полагать , то отсюда вытекает
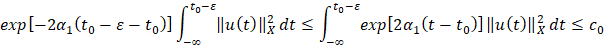
или
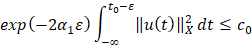 .
.
Отсюда следует
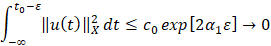 при
при 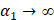 . Таким образом,
. Таким образом, 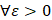 .
. 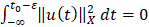 , что означает равенство почти всюду решения
, что означает равенство почти всюду решения 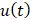 в
в 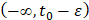 . В силу произвольности
. В силу произвольности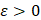
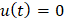 ,
, 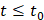 .
.
Аналогично можно показать, что 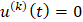 ,
, 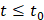 ,
, 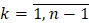 .
.

.png&w=640&q=75)