Для определения степени влияния на время отрыва частицы от лотка различных факторов рассмотрим схему сил, действующих на частицу, находящуюся в слое материала [1]. Движение частицы относительно вибрирующей по гармоническому закону перфорированной поверхности с учетом фильтруемого через слой материала в системе координат, связанной с этой поверхностью, описывается уравнениями (рис. 1):
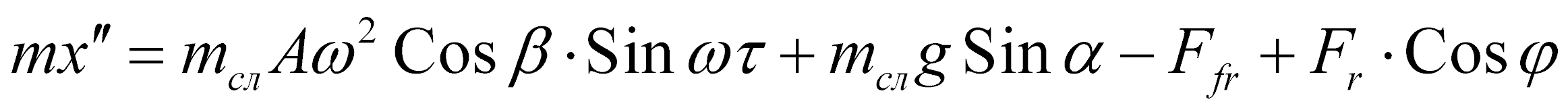(1)
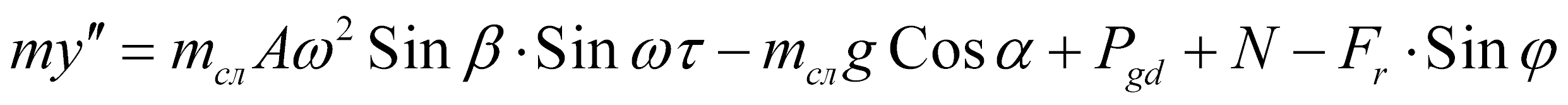, (2)
где Fr – сила сопротивления, учитывающая влияние “присоединенной” массы и внутреннего трения в слое материала; j – угол наклона результирующей силы сопротивления относительно лотка; N – нормальная реакция лотка.
Рис. Схема сил, действующих на частицу
Под «присоединенной» массой понимается масса частиц, находящихся выше рассматриваемой частицы.
Если частица находится на лотке без отрыва, то ее ускорение относительно этой поверхности равно нулю. Отрыв частицы от поверхности произойдет, когда выполнится условие N=0. Исходя из этого, получим зависимость для определения времени отрыва частицы от лотка с момента начала движения:
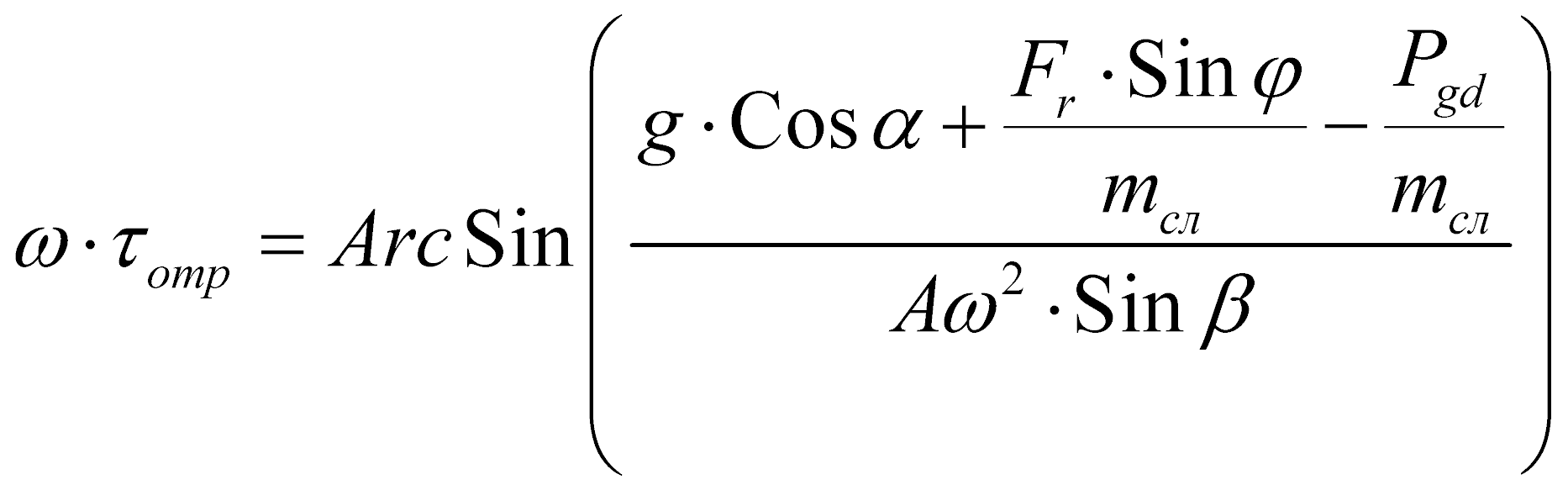(3)
Масса слоя частиц, находящихся на расстоянии h от верхней границы слоя материала до рассматриваемой частицы:
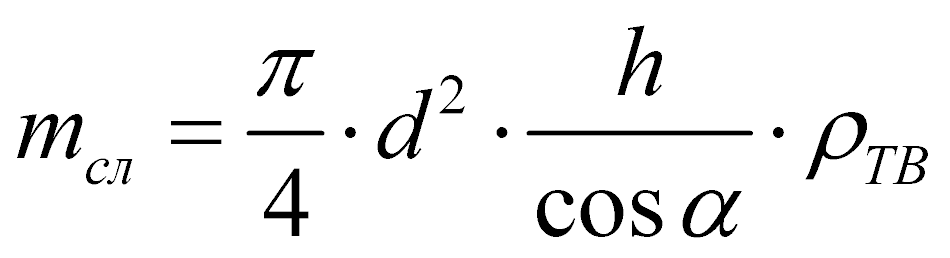(4)
Сила тяжести рассматриваемого слоя частиц
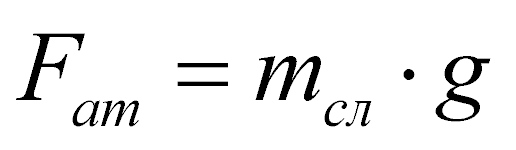(5)
Сила сопротивления внутреннего трения:
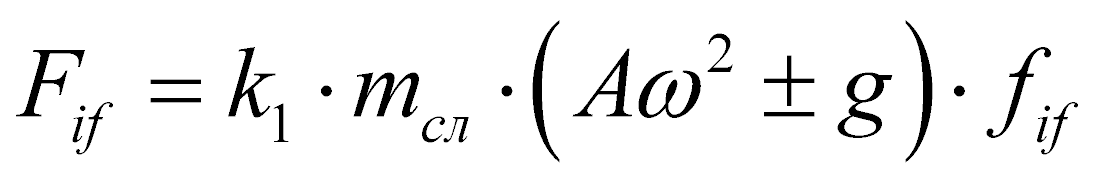, (6)
где k1 – поправочный коэффициент; fif – коэффициент внутреннего трения.
Тогда результирующую силу сопротивления можно определить из соотношения:
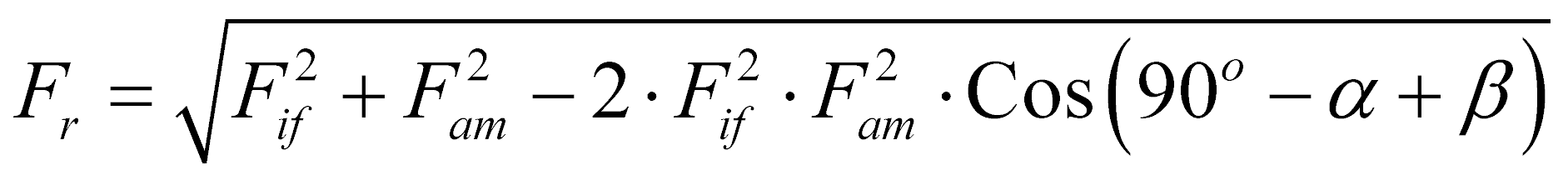(7)
Рgd – гидродинамическая сила потока воздуха, действующая на частицу:
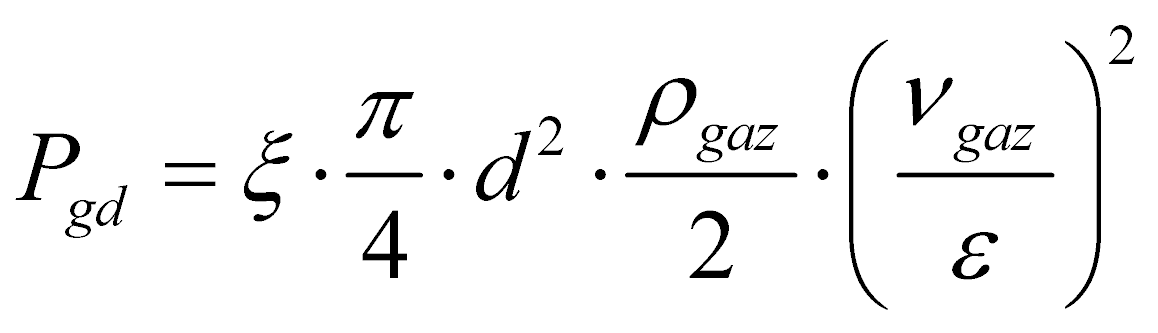, (8)
где ξ коэффициент сопротивления, зависящий от режима движения и скорости теплоносителя в пространстве около частицы. рассчитывается по зависимостям ξ=f(Re) для внешней задачи обтекания твердой частицы потоком газа [2].
После отрыва от основного слоя «верхних» частиц, расположенные ниже частицы оказываются в условиях «верхних».
Таким образом, процесс отрыва частиц материала от вибрирующего лотка развивается лавинообразно от верхних слоев к нижним с конечной скоростью.
Время отрыва частицы от лотка предлагается рассчитывать по модифицированной зависимости
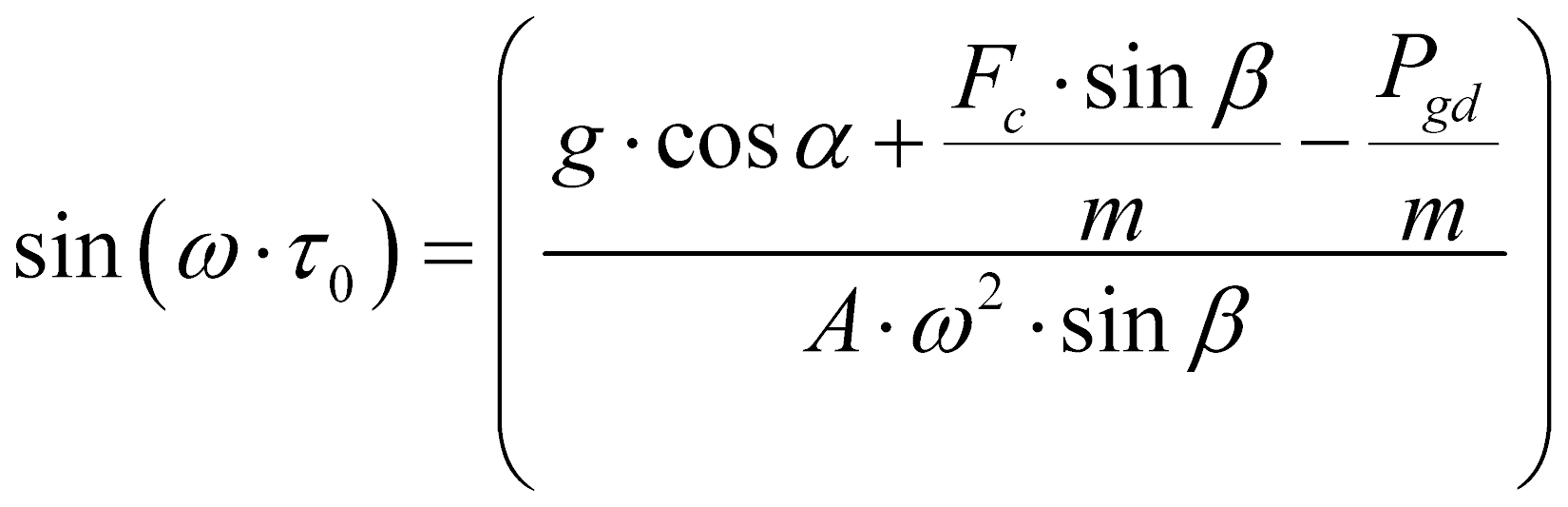, (9)
где Fc – сила сопротивления, препятствующая возможному перемещению частицы в направлении «от лотка» за счет как механического зацепления неровностями на поверхности частиц, так и за счет поверхностных сил сцепления, возрастающих с увеличением дисперсности материала.
Оценку Fc возможно провести по выражению
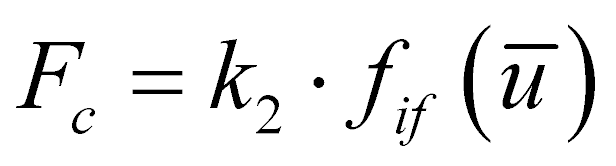, (10)
где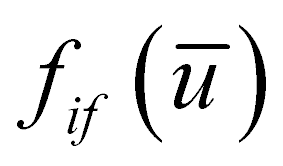 
– коэффициент внутреннего трения материала, зависящий от влажности; k2 – поправочный коэффициент, учитывающий уменьшение сил внутреннего трения в процессе образования виброаэрокипящего слоя. Значение k2 предполагается установить в ходе идентификации математической модели.
Движение частицы после отрыва от лотка в условиях вязкой среды можно описать следующими дифференциальными уравнениями:
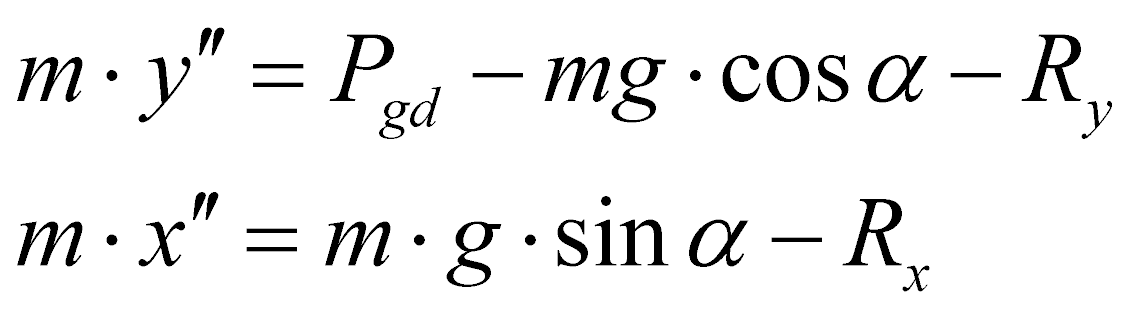, (11)
где Rx,y - соответствующие проекции силы сопротивления, на оси координат.
Для описания силы сопротивления движению частицы после отрыва ее от лотка условно используется формула Стокса для движения одиночной частицы в вязкой среде:
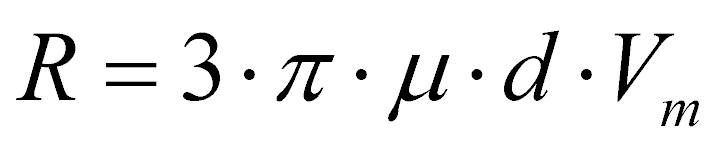, (12)
где m - эффективная вязкость виброаэрокипящего слоя, учитывающая параметры вибрационного воздействия, скорость продуваемого через слой газа, физико-механические характеристики материала.
В момент отрыва частицы от лотка скорости собственно частицы и газораспределительной решетки практически равны, поэтому можно принять начальную скорость частицы, равной скорости лотка в момент отрыва частицы от него, то есть
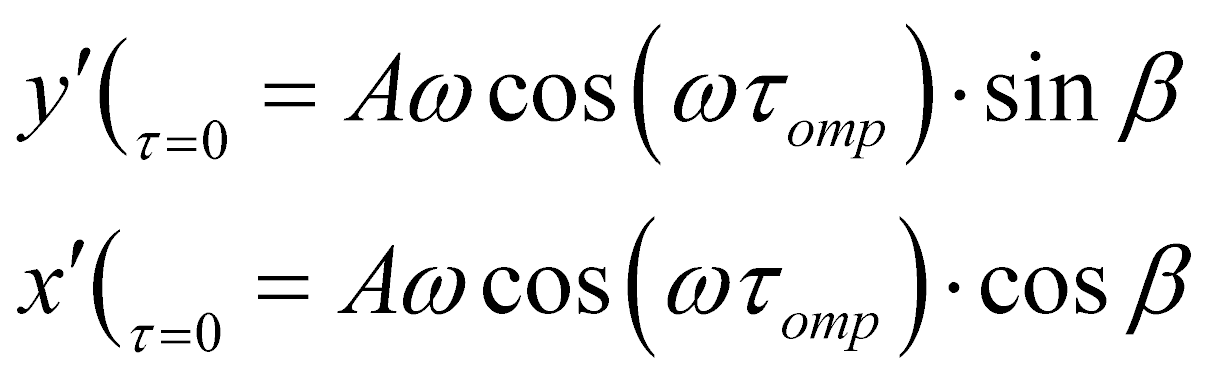(13)
Интегрируя уравнения (10), с учетом (11 - 12), получим следующие аналитические зависимости:
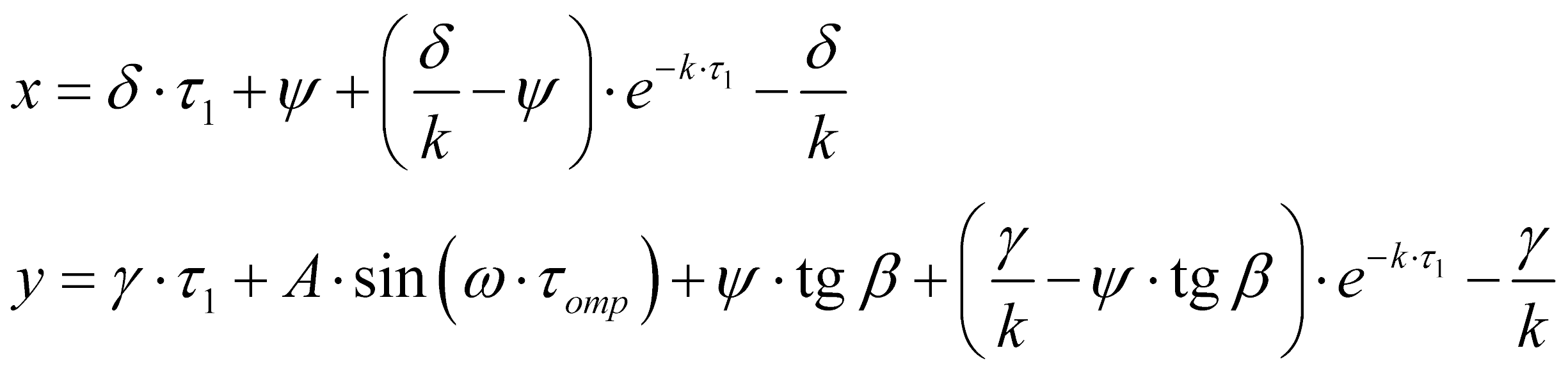, (14)
где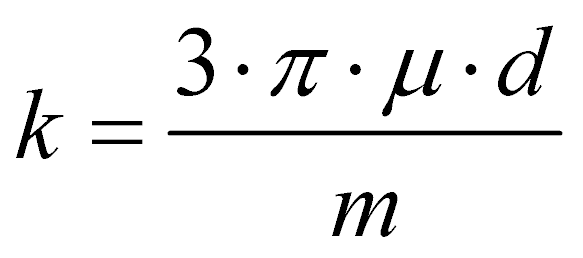 
, 
,
, 
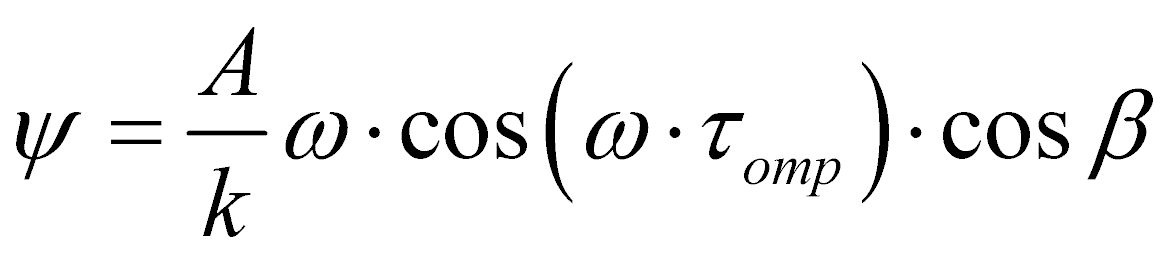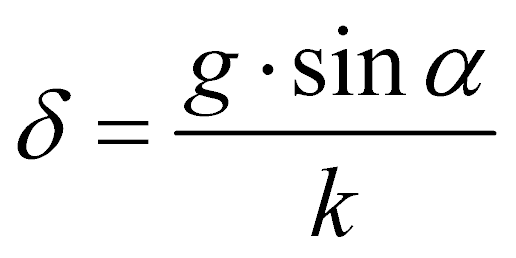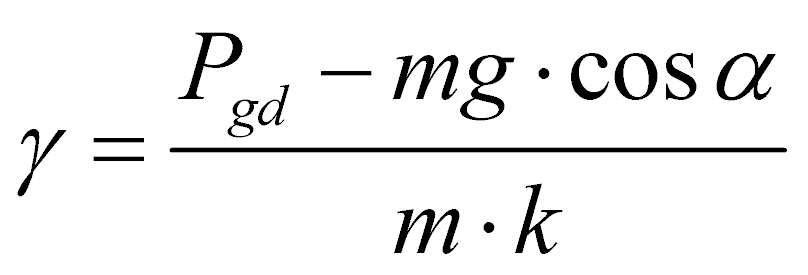; t1 – время движения частицы после отрыва ее от лотка.
Скорость перемещения частицы по лотку при виброаэрокипении определяется как отношение перемещения частицы по координате х к длительности периода колебаний лотка
Условие касания частицей лотка выражается равенством
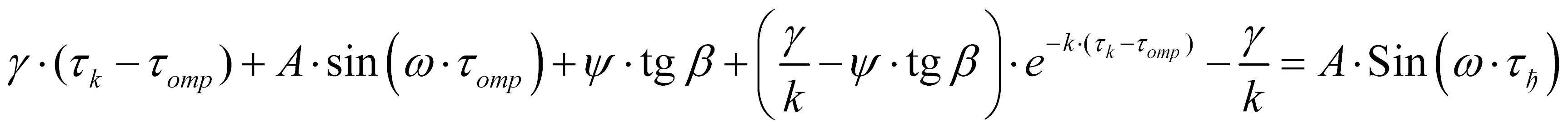(15)
Таким образом, скорость частицы определяется по зависимости
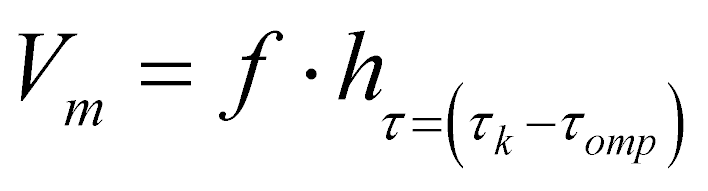, (16)
где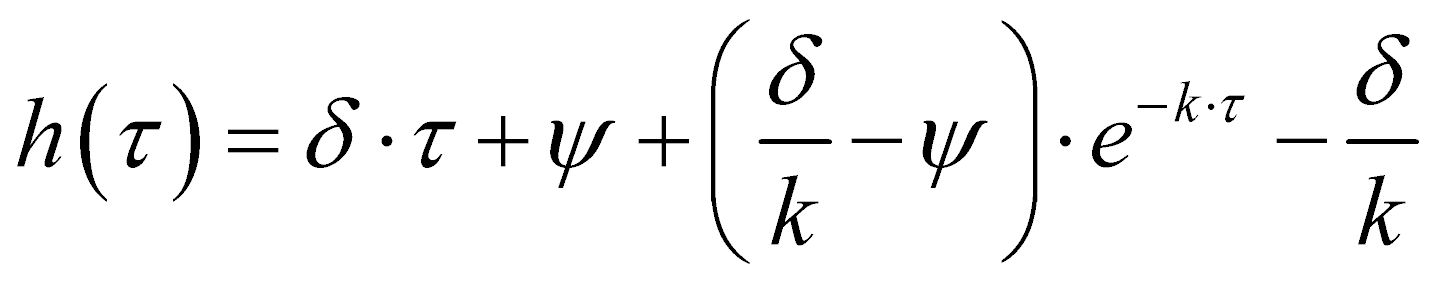 
- перемещение частицы вдоль лотка за время одного периода колебаний.
.png&w=640&q=75)
