Использование метода декомпозиции в решении показательных и логарифмических неравенств

При решении неравенств методом интервалов вычисление значений функций в промежуточных точках может вызвать трудности вычислительного характера. С другой стороны, применение свойства знакочередования рациональной функции сводит вычисления до минимума.

Чтобы расширить возможности применения метода интервалов при решении неравенств, используем идею рационализации неравенств, известную в математической литературе под другими названиями.

Метод рационализации заключается в замене сложного выражения F(x) на более простое выражение G(x) (в конечном счете, рациональное), при которой неравенство G(x)>0 (G(x)<0) равносильно неравенству F(x)>0 (F(x)<0) в области определения выражения F(x). В этом случае будем говорить, что выражение G(x) является рационализацией (или рационализирующим выражением) для выражения F(x).

Идея метода рационализации состоит в использовании свойств монотонной функции [4, с. 288].

Сначала напомним теорему о корне монотонной функции.

Теорема. Если p(x) – функция, монотонная на промежутке M, и E(p) – множество ее значений на этом промежутке, то для любого числа c∈E(p) существует и притом единственный корень x₀∈M 0x M – уравнения p(x)=c.

Следствие 1. Если p(x) – возрастающая функция на промежутке M, то для любых чисел x₁,x₂∈M неравенства p(x₁)≥p(x₂) и x₁≥x₂ равносильны, или p(x₁)-p(x₂)≥0<  = >x₁-x₂≥0 (аналогично (x₁)-p(x₂)>0<  = >x₁-x₂>0).

Отметим, что функции p(t)=log_at и p(t)=a^t являются монотонными на всей своей области определения, причем при a>1 они являются возрастающими, а при 0<a<1 – убывающими.

Рассмотрим знаки выражений F(x)= log_af(x)-log_ag(x), fx-g(x) и G(x)=(a-1)(f(x)-g(x))  в зависимости от a на области определения F(x), заданной системой неравенств

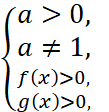    (1)

где f(x),g(x) функции, a основание логарифма.

Таблица 1

Зависимость основания a от логарифмических функций

Источник: учебное пособие «Решение показательных и логарифмических уравнений, неравенств и систем уравнений повышенного и высокого уровня сложности (Часть 2)

Из таблицы следует, что выражения  F(x) и G(x) при всех допустимых значениях x имеют одинаковые знаки.

Полученный результат запишем в виде теоремы.

Теорема 1. При a>0 и a≠1 знаки выражений  log_af(x)-log_ag(x) и (a-1)(f(x)-g(x)) совпадают для всех значений x таких, что f(x)>0 и g(x)>0.

Поскольку при a>0 и a≠1 и всех допустимых значениях x справедливы равенства:

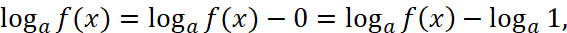
то получаем следующие следствия из теоремы 1.

Следствие 1. При a>0 и a≠1 знаки выражени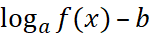й

 и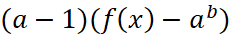

совпадают для всех значений x таких, что f(x)>0.

Следствие 2. При a>0 и a≠1 знаки выражений

log_af(x) и (a-1)(f(x)-1)

совпадают для всех значений x таких, что fx>0.

Замечание. Для выражения  или  рационализацией является выражение 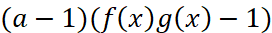 при условиях (2).

Метод рационализации используют при решении неравенств вида F(x)∨0, где символ ∨ означает один из знаков неравенств ≥,≤,>,<, в которых выражение F(x) удается рационализировать, либо выражение

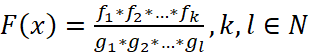     (2)

записано в виде произведения или частного выражений, каждое из которых можно рационализировать.

Например, при соответствующих ограничениях на переменную x:

• неравенство 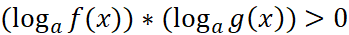 равносильно неравенству

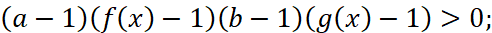
• неравенство 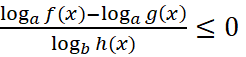 равносильно неравенству

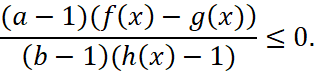
Стандартные ошибки, которые допускают учащиеся при использовании метода рационализации, заключаются в следующем:

• проводят рационализацию без учета области определения данного неравенства;
• применяют метод рационализации к неравенствам, не приведенным к стандартному виду F(x)∨0;
• формально применяют метод рационализации к выражениям вида log_af(x)+log_ag(x), заменяя на выражение f(x)+g(x) (см. выше замечание);
• подменяют формулировку «о совпадении знаков выражений для каждого допустимого значения x» на неверную формулировку «о совпадении значений выражений для каждого допустимого значения x».

Рассмотрим теперь неравенства, содержащие логарифмы с переменным основанием и выражения под знаком логарифма, содержащие функции, зависящие от x.

Теорема 2. Знаки выражений

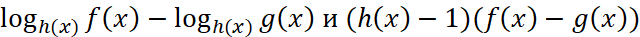
совпадают для всех значений x таких, что

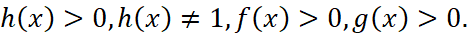
Следствие 1. Знаки выражений

совпадают для всех значений x таких, что

Следствие 2. Знаки выражений

совпадают для всех значений x таких, что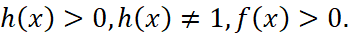 

Теорема 3. Знаки выражений

log _f(x)hx-log _g(x)h(x) и  

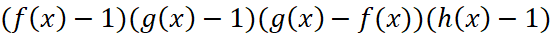
совпадают для всех значений x таких, что

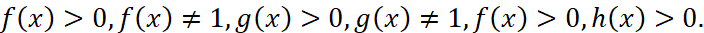
Теорема 4. Знаки выражений

 совпадают для всех значений x таких, что h(x)>0.

Следствие 1. Знаки выражений h(x)_f(x)-1 и (hx-1)*f(x) совпадают для всех значений x таких, что h(x)>0.

Следствие 2. Для числа a>0 знаки выражений a^f(x)-a^g(x) и

(a-1)(f(x)-g(x)) совпадают для всех допустимых значений x.

Теорема 5. Знаки выражений f(x)^h(x)-g(x)^h(x) и (f(x)-g(x))h(x) совпадают для всех значений x таких, что f(x)>0, g(x)>0.

Следствие 1. Знаки выражений 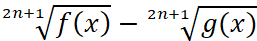 и f(x)-g(x) совпадают для всех допустимых значений x, где n∈N.

Следствие 2. Знаки выражени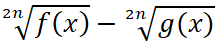й  и 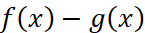 совпадают для всех значений x таких, что f(x)>0, g(x)>0, n∈N.

Теорема 6. Знаки выражений |f(x)|-|g(x)| и (f(x)-g(x))(f(x)+g(x)) совпадают для всех допустимых значений x.

Пример 9. Решить неравенство

Решение. ОДЗ данного неравенства следующее

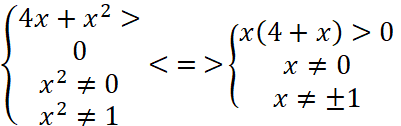
Представим решение ОДЗ на графике.

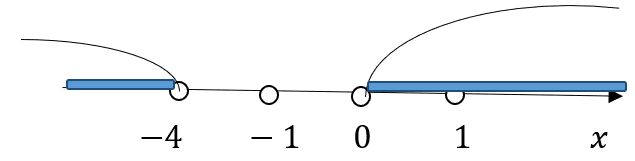
Рис. 1. Графическое изображение решения примера 9

Решая эту систему получаем следующее, что неравенство определено при всех значениях x∈(-∞;-4)∪(0;1)∪(1;+∞). Далее необходимо преобразовать исходное неравенство, насколько это возможно

Применим свойство степени логарифмируемого числа, то есть коэффициент 2 выразим как квадрат аргумента.

Числитель и знаменатель дроби разложим по формуле разность квадратов

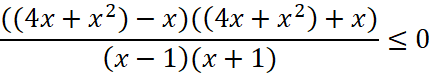
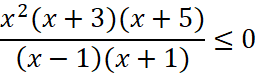
Решением данного неравенства представим графическим методом.

Рис. 2. Графическое изображение решения примера 9

x∈[-5;-3]∪(-1;1)

Учитывая ранее найденное ОДЗ текущего неравенства ответ представим на графическом рисунке.

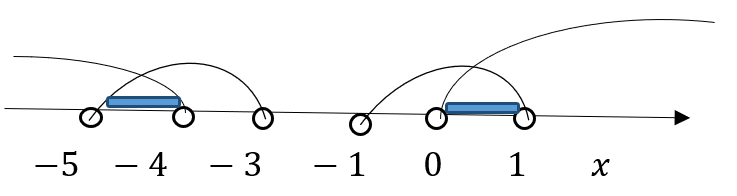
x∈[-5;-4)]∪[0;1)

Ответ. x∈[-5;-4)]∪[0;1)

Таблица 2

Основные выражения F и соответствующие им рационализирующие выражения G при соответствующих ограничениях на переменную x

Источник: Учебное пособие «Решение показательных и логарифмических уравнений, неравенств и систем уравнений повышенного и высокого уровня сложности (Часть 2).