Влияние ветра на траектории корректируемого артиллерийского снаряда

Введение

В настоящее время управления траектории полёта летательного аппарата (ЛА) рассматривается вектор ошибки попадания его объекта, однако в настоящее время вне рассматривается физик летательного аппарата, это параметр оказывает влияние на летательный аппарат (ЛА). Значительное влияние на распределение параметров атмосферы оказывает перемещение воздушных масс – ветры [1].

Уравнения движения неуправляемой ракеты в плоско-параллельном гравитационном поле

При отсутствии управления полет ракеты становится неуправляемым. Неуправляемые ракеты предназначаются для стрельбы на сравнительно небольшие дальности, поэтому во многих случаях можно не учитывать кривизну поверхности Земли. При решении задач часто применяется система уравнений, написанная в естественной системе координат [2]. Если учесть, что при малых углах атаки sinα≈α,cosα≈0 и Y=0 добавить обычные кинематические соотношения, то получим искомую систему уравнений, описывающую движение центра масс неуправляемой ракеты

; ;

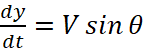; .    (1)

При принятых допущениях векторы силы тяги, лобового сопротивления и скорости центра масс лежат на одной прямой (рис. 1) [3].

Рис. 1. Упрощенная схема сил, действующих на материальную точку, совпадающую с центом масс неуправляемой ракеты

Ветра

Выбор траектории летательного аппарата (ЛА), его динамических характеристик, а также решение всей совокупности задач баллистического и навигационного обеспечения в значительной степени зависят от физических условий полета. Характер и интенсивность взаимодействия с воздушной средой определяются такими же параметрами, как состав, плотность, давление, температура, скорость распространения возмущений и т.п.

В данной работе исследованы параметры точки падения двухступенчатой ракеты с учетом влияния различной ветровой нагрузки.

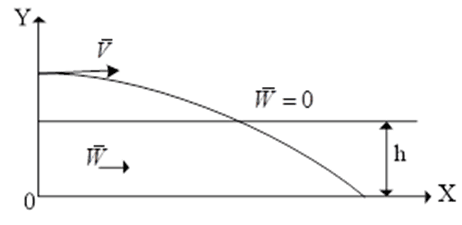
Модель распределения ветра представлена на рис. 2.

а

б

Рис. 2. Модель распределения ветра в плоскости X0Y: для исследования влияния ветра (а) на конечном участке, (б) на всей траектории ракеты

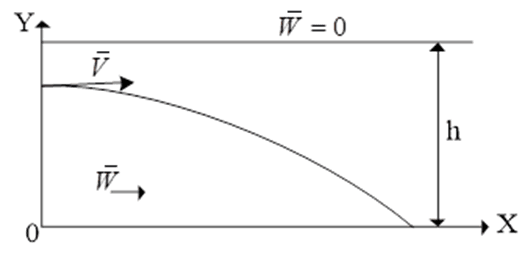
При проведении расчетов вектор скорости ветра раскладывают по направлению стрельбы (так называемый продольный ветер) и по нормали к нему (боковой ветер) [4] в проекциях на оси нормальной СК

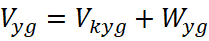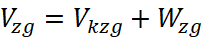; ; .    (2)

Проецируем векторы скоростей на оси траекторной системы координат, получим

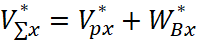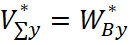; ; .     (3)

Отсюда найти

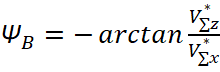; .    (4)

Влияние ветра на всей траектории

При дальности до цели D_о=4123m; W_Bg=19m/c; θ_Bg=0^o.

При дальности до цели D_о=4123m; W_Bg=10m/c; θ_Bg=0^o.

При дальности до цели D_о=3162m; W_Bg=19m/c; θ_Bg=0^o.

Рис. 3. Эллипс рассеивания точек падения ракеты в зависимости от величины угла ветра при различных расстояниях до цели D₁=3162m и D₂=4123m

Влияние ветра на конечном участке траектории

Рис. 4. Зависимость угол поправки от дальности до цели для Ψ_B=-90⁰

Заключение

На всей траектории:

1. Уменьшение постоянной составляющей ветра приводит к отклонению точки падения от номинальной по линейной зависимости. Продольный ветер не влияет на движение ЛА в боковом направлении, а боковой только при небольших значениях ветра не влияет на продольное отклонение;
2. Уменьшение дальности до цели при основной составляющей ветра W_B=19m/c  приводит к такому же уменьшению эллипса рассеивания.

На конечном участке:

1. Увеличение высоты ветра при постоянной его скорости приводит к отклонению точки падения от номинального по линейной зависимости;
2. Боковой ветер оказывают незначительное  влияние на движение ЛА в продольном направлении, только при больших значениях длина конечного участка;
3. Продольный ветер оказывают незначительное  влияние на движение ЛА в боковом направлении.