В данной бездатчиковой системе задача состоит в том, чтобы реализовать надежный наблюдатель скорости, который может отклонять возмущения, представленных скачкообразной нагрузкой на вал синхронного двигателя.
Наблюдатель – это математическая модель технического объекта, которая позволяет по известным управляющим воздействиям и некоторым прямо измеряемых переменных состояния оценивать значения неизмеряемых переменных состояния. В данном случае при известных токах статора производится восстановление скорости электропривода во вращающейся системе координат dq.
Для построения структурной схемы синхронного электропривода требуется применить следующее уравнение модели объекта [1, с. 195]:
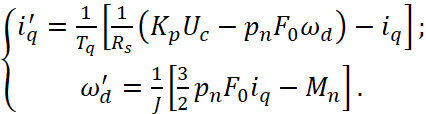(1)
Ниже представлена структурная схема модели объекта с настройкой контура скорости на симметричный оптимум [2, с. 255] в среде Matlab Simulink (рис. 1):
Рис. 1. Структурная схема модели объекта
Реакция системы на входное ступенчатое воздействие (Uc=1) в начальный момент времени и набросе статического момента нагрузки на вал синхронного двигателя в момент 0,06 с представлена ниже (рис. 2).
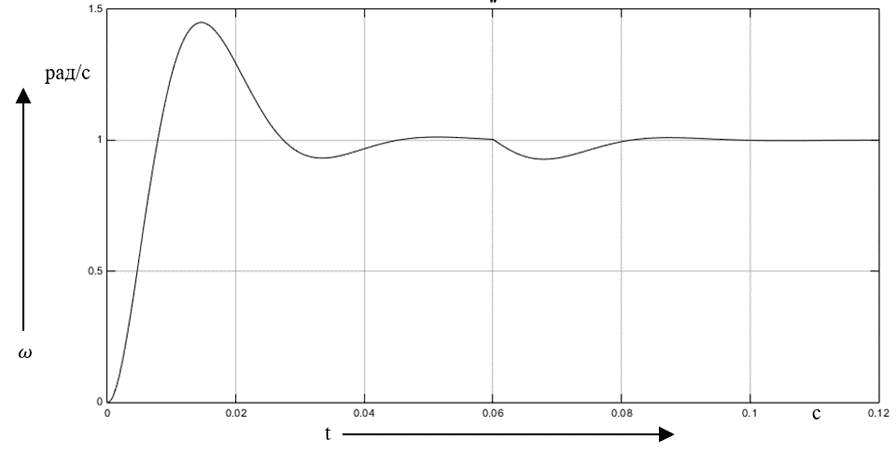
Рис. 2. Реакция скорости синхронного электропривода при ступенчатом воздействии и набросе статического момента нагрузки на вал
По графику можно сделать вывод, что перерегулирование составляет 44,95 % и время регулирования 0,0376 с, что удовлетворяет настройке системы.
Для синтеза астатического наблюдателя требуется расширенное математическое описание объекта в векторно-матричной форме записи [1, с. 195]:
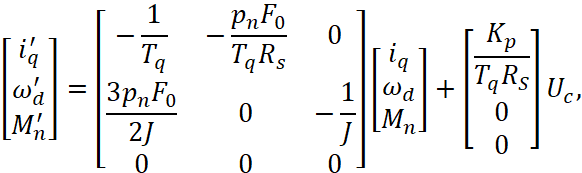
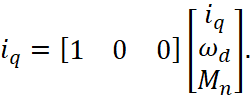(2)
Уравнение состояния наблюдающего устройства [3, с. 69]:
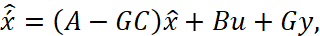(3)
где G – матрица коэффициентов наблюдателя;
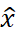– восстановленный вектор состояния.
Матрица A-GC для объекта (1) будет равна:
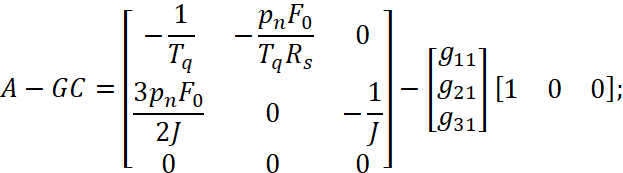
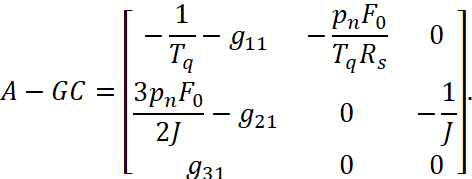(4)
Матрица pI-(A-GC) и её определитель соответственно:
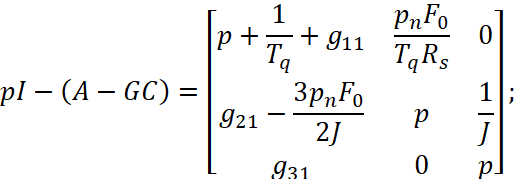(5)
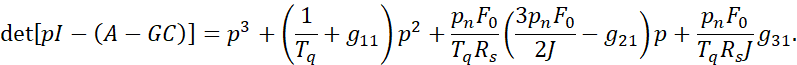
Наблюдатель настраивается на биномиальную форму (5):
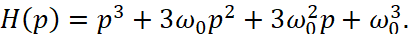
Сопоставление коэффициентов полиномов позволяет записать (4) и (5):
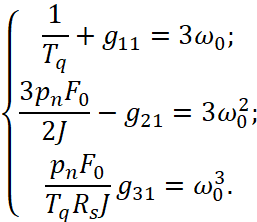
Откуда:
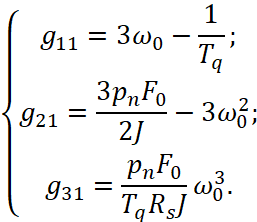
Тогда, в соответствии с уравнением (3) наблюдатель описывается уравнениями:
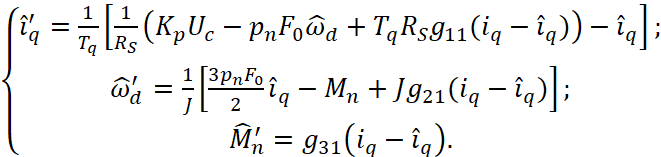(6)
По вышеуказанным уравнениям (6) реализована структурная схема синхронного электропривода с восстановлением скорости с применением астатического наблюдателя (рис. 3).
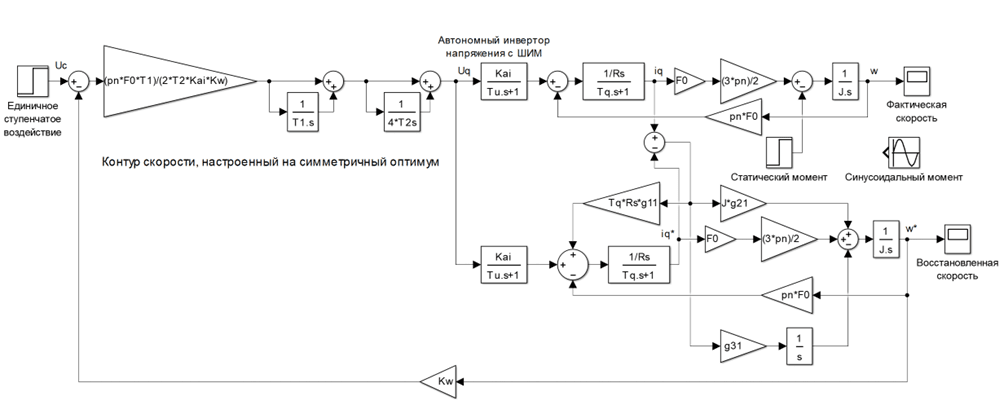
Рис. 3. Структурная схема синхронного электропривода с астатическим наблюдателем восстановления скорости
Для оценки моделирования производится симуляция вышепредставленной математической модели системы (рис. 4).
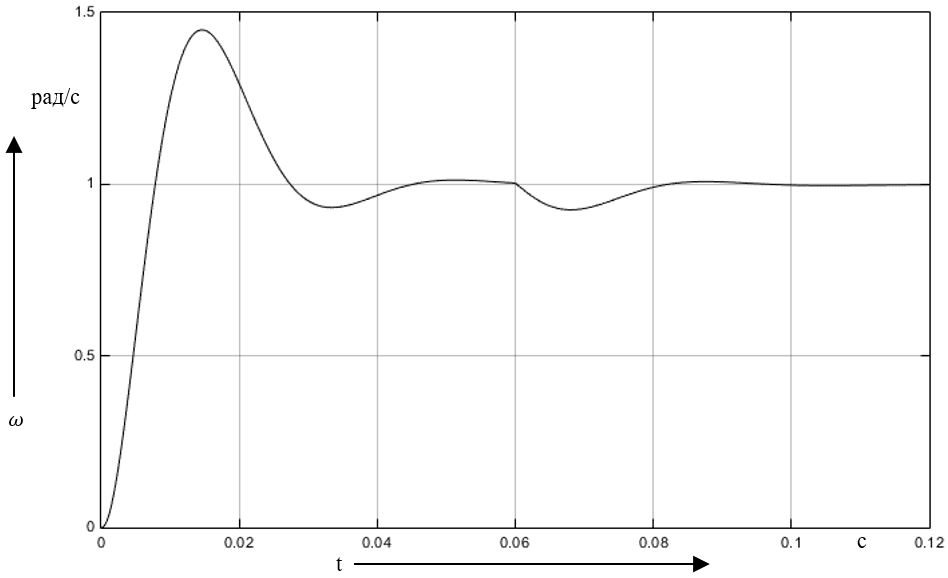
Рис. 4. Реакция скорости синхронного электропривода при ступенчатом воздействии и набросе статического момента нагрузки на вал
Результаты моделирования продемонстрировали, что перерегулирование и время моделирования остались прежними после перехода от датчика скорости к синтезированному астатическому наблюдателю скорости. Следовательно, применение в системах, где требуется датчик скорости возможно заменить на математическую модель, вычисляющую скорость по сигналам токов статора синхронного двигателя.
