Моделирование транспортно-пересадочных узлов, описание математической модели

Исследование транспортных сетей и их эффективного управления относится ко времени древних времен. Известно, например, что римляне ввели контроль над движением колесниц в разное время дня, чтобы справиться с перегруженностью.

С экономической точки зрения некоторые самые ранние работы над этой темой касаются Коля (1841) и Pigou (1920), кто рассмотрел транспортную сеть с двумя узлами, определенную перегруженность как проблема и признал, что могут преобладать различные поведенческие понятия относительно выбора маршрута.

Формальное исследование сетей транспортировки бросило вызов ученым транспортировки, экономистам, операционным исследователям, инженерам и физикам по следующим причинам: размер и объем систем включены; поведение сетевых пользователей, которые могут измениться в зависимости от параметров приложения, приведя к различному понятию optimality/equilibrium; различные классы большинства пользователей могут по-разному, чтобы чувствовать стоимость использования сети, и перегруженность играет все больше важная роль во многих транспортных сетях.

Считается, что пробка на дороге приводит к потере производительности приблизительно $100 миллиардов в одних только Соединенных Штатах, в то время как в Европе это число – приблизительно $150 миллиардов, и в России – $15 миллиардов, в то время как ожидается, что к 2030 количество автомобилей увеличится на 50 процентов в год и удвоит к 2050 год. В частности, увеличивающееся использование моторизованных транспортных средств, особенно легковых автомобилей, в развивающихся странах преобразовывает страны, такие как Китай и Индия. Кроме того, во многих современных транспортных сетях, «несовместное» поведение пользователей усиливает проблему пробок. Например, в случае городских транспортных сетей, путешественники выбирают свои маршруты от пункта отправления до места назначения таким способом как, чтобы минимизировать их собственные транспортные расходы или время прохождения, которое, хотя оптимальный с точки зрения пользователя (пользовательская оптимизация), может не быть оптимальным с точки зрения пользователя. С социальной точки зрения (системная оптимизация), когда решение производителя или центральный диспетчер управляют потоками в сети и стремятся распределить потоки таким способом как, чтобы минимизировать общую стоимость в сети.

В сочетании с пробкой на дороге, увеличениями загрязнения окружающей среды, который является другим отрицательным внешним фактором, что дальнейшее влияние мир, в котором мы живем. Известный пример Парадокса Брасса (1968) иллюстрирует в бетоне и поразительном пути различие между некооперативом (или оптимизированный пользователями) поведение и оптимизированным системой поведением. В этом примере предполагается, что главный поведенческий принцип – пользовательская оптимизация, и путешественники выбирают свои маршруты соответственно. В сети Брасса, добавляя новую дорогу, не изменяя спрос на путешествие приводит к увеличению стоимости путешествия на всех путешественников в сети. Реальные примеры этого явления были определены в Нью-Йорке и Штутгарте, Германия. В 2005 42-я улица в Нью-Йорке была закрыта для Дня Земли, и транспортный поток в области улучшился. В Штутгарте, в свою очередь, новая дорога была построена к центру города, но трафик ухудшился и после жалоб, новая дорога была уничтожена. Подобный опыт был недавно обнаружен в Сеуле, Корея. Интересно, это явление также относится к телекоммуникационным сетям и, в частности, к Интернету. Этот результат не достигнут в оптимизированных системой сетях, где добавление новой дороги/связи, если используется, уменьшило бы общую стоимость сети. Прогрессивная шкала дорожных взносов – активная тема исследования сегодня, и коллекция потерь успешно улучшила трафик, изменив поведение 4 человек в различных городах во всем мире, включая получивший широкую огласку опыт Лондона, Соединенное Королевство.

Эксперимент проводился на основе городской системы общественного транспорта санкт-петербургского скопления. Одной из таких моделей является модель неоднородного транспортного потока, допускающая разнообразие транспортной ситуации. Ситуация на дорогах естественным образом меняется из-за препятствий, кривизны, количества полос, ограничений скорости и других факторов. Предлагаемая нами неоднородная модель представляет собой систему нелинейных гиперболических уравнений, в которой течение и начальные условия зависят от пространственной переменной. Показано глобальное существование решений и их сходимость к решению уравнения равновесия, поскольку время релаксации стремится к нулю.

Кроме того, изучается модель транспортного потока с невогнутой фундаментальной диаграммой. Модель представляет собой систему несгибаемых гиперболических законов сохранения с релаксацией. В реальном транспортном потоке есть развернутая фундаментальная диаграмма.

При такой постановке задачи сравнительный анализ объема трансфертного пассажиропотока в зависимости от времени, затраченного на посадку (пересадку), является основой для определения эффективности размещения ТПУ [2], под которыми понимаются комплексы реальных объекты недвижимости, в том числе земельный участок или несколько земельных участков с расположенными на них, над или под ними объектами транспортной инфраструктуры, а также иными сооружениями, предназначенными для обеспечения безопасного и комфортного обслуживания пассажиров в местах пересадки с одного вида транспорта на другой без пересечения пассажиропотоков.

В результате изучения транспортных потоков высокой плотности и специальных экспериментов, проведенных американскими специалистами, была предложена теория «следования за лидером», математическим выражением которой является микроскопическая модель транспортного потока. Он называется микроскопическим, потому что рассматривает элемент потока – пару автомобилей, следующих друг за другом. Особенность этой модели в том, что она отражает закономерности комплекса ВАДС и, в частности, психологический аспект вождения автомобиля. Он заключается в том, что при движении в плотном транспортном потоке действия водителя обусловлены изменением скорости ведущего (лидирующего) автомобиля и расстояния до него в данный момент.

Экспериментальная проверка основного уравнения проводилась несколькими учеными с использованием натурного имитационного эксперимента с использованием двух автомобилей, оснащенных оборудованием для измерения значений параметров уравнения. Расстояние между автомобилями определялось киносъемкой или специальной амортизирующей лебедкой, соединявшей оба автомобиля. Однако такой эксперимент уже в своей постановке содержит некоторую искусственность, искажающую реальный процесс. Заключается это, в первую очередь, в специальном подборе водителей, автомобилей и установке определенного режима вождения. Кроме того, относительно небольшое количество измерений не позволяет охватить все многообразие ситуаций, возникающих в реальном транспортном потоке. Дорожные условия и общая транспортная ситуация рассматриваются в этой модели не как отдельные параметры, а как проявляющиеся в величине скорости движения. Уравнение теории следования за лидером описывает взаимодействие между автомобилями с учетом реакции водителя на изменения транспортного потока, называемые раздражителями. К математическим моделям, рассматривающим течение как единое целое и называемым макроскопическими, относятся, например, модели гидродинамической теории.

Наиболее известны два из них, основанные на использовании аналогии в поведении транспортного потока и потока жидкости. Первый основан на уравнении неразрывности, определяющем постоянство количества жидкости при ее протекании через сток, а в принятых для транспортного потока обозначениях в результате преобразований и упрощений характеризуется зависимостью:

,

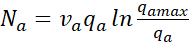
где v_a – скорость, подлежащая экспериментальному определению; q_а mах – плотность транспортного потока при заторе (v_a = 0).

Вторая гидродинамическая модель использует известное из гидравлики понятие потенциала давления жидкости и предполагает, что движение автомобиля выражается функцией определенного потенциала давления в зависимости от дорожных условий, состояния окружающей среды и психофизиологического состояния водителя.

Для решения некоторых задач управления дорожным движением необходимо иметь стохастические характеристики параметров транспортного потока в зоне перекрестка или на других контролируемых участках дороги. Исследованиями установлено, что уравнение (распределение) применимо для описания потоков относительно малой интенсивности, характеризующих вероятность проезда определенного числа транспортных средств через участок дороги Пуассона:

,

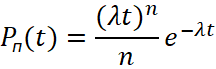где P_n(t) – вероятность проезда n-го числа автомобилей за время t; λ – основной параметр распределения (интенсивность транспортного потока), авт. с; t – длительность отрезков наблюдения, с; n – число наблюдаемых автомобилей.

Указанные модели совпадают с натурными наблюдениями для однородных потоков, состоящих в основном из легковых автомобилей. При смешанном течении, а также при воздействии некоторых внешних факторов распределение Пуассона не дает удовлетворительных результатов, и в этом случае можно применить гамма-распределение Пирсона III типа или распределение Эрланга.

Движение транспортных средств по дорогам с интенсивным потоком и особенно в зоне пересечения можно рассматривать на основе теории массового обслуживания. Задачи, решаемые с помощью этой теории, обычно сводятся к определению максимального количества «заявок», а также определению очереди в системе через определенный промежуток времени. Применительно к транспортной задаче это означает возможность определения пропускной способности проезда, задержек автомобилей и возникающих перед перекрестком очередей. Под «заявкой» понимается появление одиночного транспортного средства на поперечном сечении дороги.

При анализе закономерностей движения, а также при решении практических задач ОДД возникает необходимость использования взаимозависимостей характеристик транспортного потока. Зависимость между интенсивностью, скоростью и плотностью движения на одной полосе дороги можно графически изобразить в виде так называемой схемы основного движения (рис. 1), отражающей зависимость:

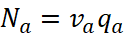
Основная диаграмма отражает изменение состояния однорядного транспортного потока преимущественно легковых автомобилей в зависимости от увеличения его интенсивности и плотности. Левая часть кривой (показана сплошной линией) отражает стационарное состояние потока, при котором по мере увеличения плотности транспортный поток проходит фазы свободного, затем частично связного и окончательно связного движения, достигая точки максимально возможной интенсивности, т.е. пропускной способности (точка N_max = Р_a на рис. 1). В процессе этих изменений скорость потока падает – она характеризуется тангенсом угла наклона а радиус-вектора, проведенного от точки 0 к любой точке кривой, характеризующей изменение N_a. Соответствующие точке N_a max = Р_a значения плотности и скорости потока считаются оптимальными по пропускной способности (q_а опт и v_a опт). При дальнейшем росте плотности (за точкой Р_а перегиба кривой) поток становится неустойчивым (эта ветвь кривой показана прерывистой линией).

Рис. 1. Основная диаграмма транспортного потока: Z – коэффициент (уровень) загрузки

Переход потока в неустойчивое состояние происходит из-за несинхронности действий водителей по соблюдению безопасной дистанции (тормозно-разгонных действий) на любом участке пути и особенно проявляется в неблагоприятных погодных условиях. Все это создает «пульсирующий» (нестабильный) поток.

Таким образом, одним из критериев выборки является коэффициент влияния величины задержки на размер пассажиропотока («показатель устойчивости»):

,

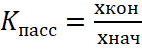где x_нач и x_кон – значения величины пассажиропотока в эксперименте при крайних значениях времени задержки на входах станций метро и пригородной железной дороги.

Этот коэффициент можно интерпретировать как показатель устойчивости (востребованности при сложившемся расселении и размещении районов тяготения) узла, т.е. станций со значительным, максимально стабильным потоком, на базе которых целесообразно формирование транспортно-пересадочных узлов.

Как указано выше, на дугах графа сети ГОТ создавались искусственные задержки на вход для станций метрополитена в диапазоне от 3 до 30 мин (от 3 до 15 мин с шагом 2 мин). Это позволило классифицировать станции по востребованности в зависимости от затрат времени на ожидание, чтобы выявить ряд станций, претендующих на роль ТПУ-образующих (таблица 1). Решив аналогичную задачу для станций пригородной железной дороги, с учётом задержек на вход, равных 10, 20, 40 и 110 мин., можно определить приоритетные места формирования ТПУ на базе железнодорожных станций (см. таблицу 1).

Таблица 1

Сводная таблица потенциально значимых узлов для размещения ТПУ, образуемых на базе станций метрополитена и станций пригородной железной дороги (значения Kпасс находятся в диапазоне от 0,7 до 1,2)

Так, с помощью предложенной методологии было выявлено 20 потенциально значимых узлов (см. таблицу 1), в которых пассажиропоток является значительным и постоянным («стабильные» станции). Для идентификации мест расположения ТПУ нахождение «показателя устойчивости» в диапазоне от 0,7 до 1,2 показывает места незначительного изменения пассажиропотока (пассажирооборота), что является одной из основных характеристик мест расположения ТПУ, свидетельствующих о стабильном спросе [3].

Введенное понятие «стабильность» узла – это уровень востребованности станции при текущем заселении и размещении гравитационных зон, который слабо зависит от временных задержек входа, т.е. «стабильные» узлы – это узлы со значительным, почти постоянный поток, на базе которого целесообразно формировать транспортно-пересадочные узлы. Основным показателем устойчивости станции является коэффициент влияния задержки на величину пассажиропотока («показатель устойчивости»). Кпасса. Для оценки на реальных дорогах (или отдельных полосах проезжей части) имеющегося запаса пропускной способности используется коэффициент Z, равный отношению существующей интенсивности движения N_ф к пропускной способности Р_ф, т.е. Z = N_ф/Р_ф (см. рис. 1). Этот коэффициент также называют уровнем загрузки дороги (полосы) транспортным потоком.

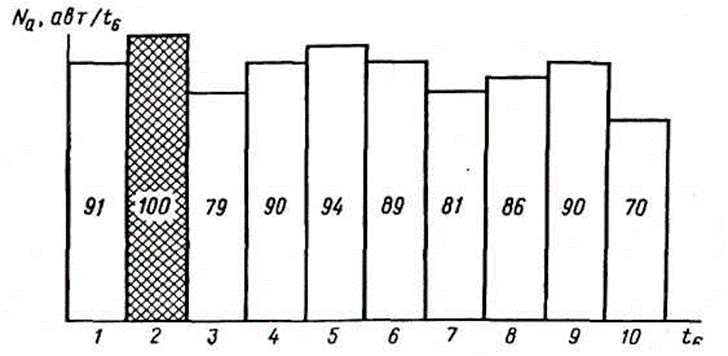
Рис. 2. Диаграмма интенсивности однорядного потока, полученная при определении коэффициента загрузки Z (no 6-минутным отрезкам времени)

Примерное значение Z может быть определено экспресс-методом часового наблюдения на элементе УДС в пиковый период движения без затора. В течение часа по 6-минутным отрезкам времени t₆ фиксируется интенсивность движения. Диаграмма на рис. 2 иллюстрирует полученные данные на одной полосе правоповоротного (нерегулируемого) потока. По наибольшей интенсивности (N_a2 ⁼ 100 авт/ч) определяется фактическая пропускная способность участка, как 100*10=1000 авт/ч. Фактическая интенсивность равна сумме интенсивности за 10 отрезков времени: 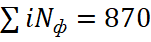авт/ч. Отсюда Z = 870/1000 = 0,87. Следовательно, данный участок работает на пределе допустимого.

Общие результаты исследования и сравнение времени, затраченного при трансплантации, со стандартными показателями представлены в таблице 2.

Из представленного образца только две станции «попали» в вышеуказанный стандарт [5]. Однако за счет оптимизации организации движения в узле с помощью устройства рационального ТПУ можно повысить эффективность его использования (см. таблицу 2).

Таблица 2

Показатели экономической эффективности при оптимизации затрат времени на пересадку в узлах

Оценка социально-экономической эффективности предлагаемых мероприятий произведена на основании стоимостной оценки затрат времени населения.

Стоимость сэкономленного времени одного пассажира находится как:

 ,

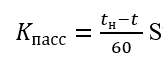где tн – нормативные затраты времени на пересадку [7], с;

t – средневзвешенные затраты времени на пересадку по обследованию, с; S – стоимость минуты рабочего времени, руб.

Стоимость сэкономленного времени всех пассажиров в узле рассчитывается путем умножения объема пассажиропотока на стоимость сэкономленного времени одного пассажира (см. таблицу 2). Результаты хронологического обследования времени, затраченного на передачу, позволяют говорить о целесообразности преобразования существующих пунктов пересадки в полноценные транспортные узлы. Ориентировочная стоимость сэкономленного пассажирами времени при установке ТПУ только в этих узлах составит более 1 млн рублей в утренний час пик.