На сегодняшний день все большее применение находят методы технической диагностики энергетического оборудования на основе вида неразрушающего контроля, а именно виброакустического контроля. Это связано с тем, что установившийся виброакустический диагностический сигнал объекта контроля обладает более полной информацией относительно его технического состояния [1].
Информацию, находящаяся в сигнале, в подавляющем большинстве случаев, характеризует амплитуда сигнала, его частота или спектральный состав. Помимо этого, информацию может охарактеризовать фаза или относительные временные зависимости нескольких сигналов. Всю эту информацию возможно извлечь из сигнала применяя методы его обработки. Для исследования возможностей методов обработки сигналов необходимо приобрести навыки в использовании систем численно – математического моделирования, таких как, MATLAB, Octave, Mathcad, LabVIEW и др.
Любой аналоговый сигнал можно подвергнуть дискретизации по времени и квантованию по уровню, а значит представить его в цифровом виде.
Существуют три основных метода обработки сигналов: аналоговый метод, цифровой метод или комбинированный метод.
Основополагающая разница между цифровой обработкой сигнала и аналоговым традиционным компьютерным анализом данных, заключается в куда большей эффективность выполнения сложных задач цифровой обработки, таких как, анализ сигнала с использованием дискретного или быстрого преобразования Фурье, алгоритмическом преобразовании данных в настоящем масштабе времени, а также скорости самих преобразований.
Комбинированная обработка сигналов подразумевает, что система может выполнять как аналоговую, так и цифровую обработку полученных вибродиагностических сигналов. Именно комбинированная обработка является наиболее распространенной из-за того, что невозможно обработать физические аналоговые сигналы, используя только цифровые методы, так как все датчики (микрофоны, термопары, манометры и т.д.) являются аналоговыми устройствами.
Наибольшую популярность приобрел метод виброакустической диагностики, согласно которому фиксируется диагностический сигнал, а в дальнейшем анализируются параметры колебаний объекта виброакустического контроля.
В целях обработки вибороакустических диагностических сигналов применяются различные методы статистики, вейвлет-преобразования, а также преобразования Фурье, которые являются одними из самых распространенных методами спектрального анализа сигналов [2].
Важно не забывать о необходимости учитывать тот факт, что при вибродиагностике наличие дефекта в структуре объекта контроля вызывает сложные динамические взаимодействия, что означает тот факт, что параметры диагностических сигналов носят хаотический характер, а это в свою очередь влияет и на сам получаемый сигнал. Из-за подобного, применение традиционных методов анализа диагностических сигналов является недостаточным. Также традиционные методы не всегда позволяют эффективно определять нерегулярные составляющие сигнала, что в следствии не дает определить дефект или неоднородность [3].
Проанализировав все вышесказанное, можно предположить, что для грамотной обработки сигнала и определения из него диагностической информации при оценке технического состояния оборудования наиболее целесообразно будет рассмотреть возможность использования энтропийных показателей, таких как энтропия Шеннона, Колмогорова, Колмогорова-Синая и других.
По итогу проведенного теоретического исследования, наиболее перспективной для изучения себя показывает энтропия Шеннона, которая дает представление о степени изменчивости процесса, другими словами, дает количественную оценку отклонения распределения значений временного ряда по уровням от равновероятного. По изменению значения энтропии Шеннона можно делать выводы относительно влияния дефекта на исследуемый сигнал. Вычисление энтропии Шеннона проводиться на основе формулы, которую в 1948 году предложил Клод Шеннон с целью вычисления информационной энтропии:
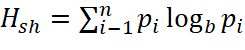 (1)
(1)
где n – количество возможных событий, b – единицы измерения информации (2 - биты, 3 – триты и т.д.), pi – вероятности события.
За исключением энтропии Шеннона одной из важнейших характеристик динамического хаоса можно принять энтропию Колмогорова. Энтропия Колмогорова определяет скорость потери информации о состоянии динамической системы по времени, но в связи с тем, что на практике временные ряды в большинстве случаев имеют конечную длину, применение энтропии Колмогорова не представляется возможным [4].
Проанализировав все вышесказанное получится сделать вывод, что присутствие дефекта в объекте контроля будет вызывать изменение собственных вибрационных параметров объекта контроля, то есть изменит распределение его энтропийных параметров, а это значит, что в соответствии будет изменено и значение энтропии. Так как энтропия Шеннона позволяет оценить степень изменчивости процессов распределения колебательной энергии, и из этого можно будет делать выводы о присутствии или отсутствии дефекта и о его влиянии на диагностический сигнал по изменению значения энтропии Шеннона.

.png&w=640&q=75)