Рассматривается трубчатый стержень конечной длины L, имеющий внутреннюю цилиндрическую и наружную коническую поверхности. Свойства материала описываются хорошо известными и широко апробированными для случаев ударного и динамического внешнего нагружения металлов и их сплавов конституционными уравнениями Малверна-Соколовского-Кристеску [1], доведенными до возможности их практического использования в работах В.Л. Баранова [2]:
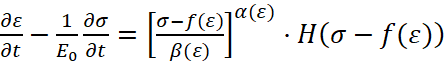, (1)
где f(ε) – диаграмма квазистатического нагружения материала;
α(ε), β(ε) – аппроксимирующие функции, характеризующие его вязкопластические свойства;
E0 – модуль упругости материала;
H(ξ) – единичная функция Хевисайда, отражающая упругий характер разгрузки материала.
В момент времени t = 0 к торцу стержня z = 0, где z – лагранжева координата, совпадающая с продольной осью симметрии стержня, в начале которой находится большее основание конуса наружной поверхности, прикладывается априори заданный импульс продольных напряжений σz(0,t). Задача решалась в тестовой постановке, для граничного условия на нагружаемом торце стержня в гипотетической форме прямоугольного импульса растягивающих напряжений вида
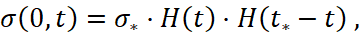(2)
где σ* – амплитуда импульса;
t* – длительность импульса напряжений. 
Начальные условия задачи соответствуют первоначально ненапряженному, недеформированному и неподвижному материалу стержня:
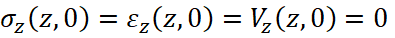. (3)
Полная система уравнений, описывающая распространение продольных волн напряжений в стержне в общем случае, соответствующем упруго-вязкопластической модели материала и геометрической неоднородности стержня, включает в себя уравнения движения материала, уравнение совместности деформаций и конституционное уравнение (1), и она является квазилинейной системой трех дифференциальных уравнений в частных производных первого порядка [1]:
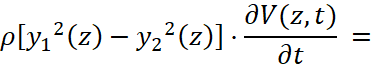
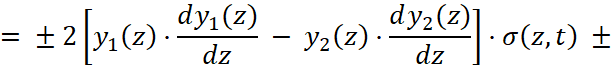
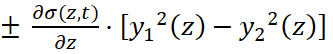, (4)
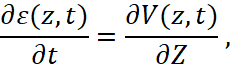
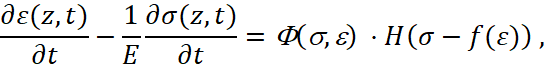
где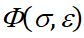 
– условное обозначение правой части конституционного уравнения (1), знак (+) в правой части уравнения движения соответствует волне растягивающих напряжений, знак (-) – случаю напряжений сжатия (в дальнейшем будет анализироваться первый случай); y=y1(z) – уравнение образующей наружной поверхности, y=y2(z) – уравнение образующей внутренней поверхности стержня.
В рассматриваемом случае
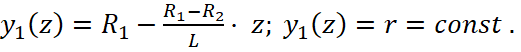(5)
Учетом (5) рабочая система уравнений (4) записывается так:
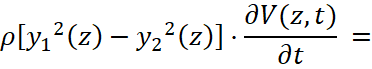
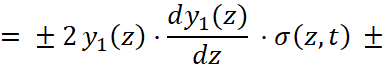
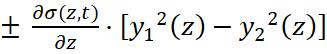, (6)
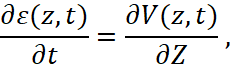
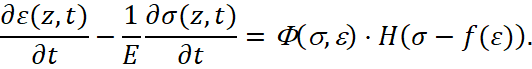
В частном случае, имеющем важное практическое приложение, параметры начальных условий и геометрия нагружаемого торца стержня таковы, что на торце формируется волна упругих напряжений, которая распространяется в геометрически неоднородный стержень. При этом упругое состояние материала ограничено сверху, то есть существуют некоторое формализованное условие, при превышении или невыполнении которого материал переходит в упруго-вязкопластическое состояние, соответствующее конституционному уравнению (1).
В этом случае система уравнений (6) вновь принимает квазилинейный вид:
,
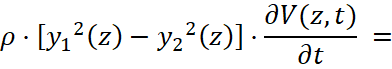
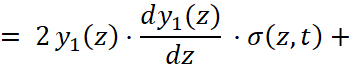
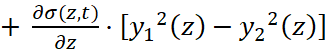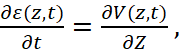(7)
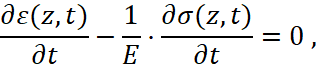
но в процессе ее решения необходимо отслеживать изменение значений напряжений и деформаций в материале стержня и производить сравнение их с критерием предельного состояния, соответствующим выходу материала из состояния упругости. Физической причиной этого перехода в такой постановке задачи будет являться геометрическая неоднородность стержня, что отражает первое слагаемое в правой части уравнения движения. Такая постановка волновой задачи, как показал проведенный анализ, является новой. Для ее численного решения разработан программный комплекс [3]. В случае выхода параметров волны в процессе ее распространения по стержню за пределы упругого состояния, то есть в случаях, когда в правой части конституционного уравнения вновь появляется функция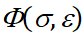 
, комплекс [3] позволяет решать и эту задачу.
Численное моделирование проводилось при следующих исходных данных:
– геометрические характеристики стержня (рисунок 1):
L=1,0 м; R2=0,08 м; r=0,05 м,
величина R1 дискретно варьировалась: R1=0,10; 0,15;0,20 м:
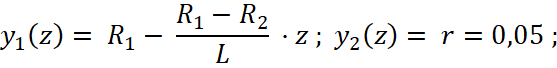
z* – продольная координата фронта волны, соответствующая моменту перехода материала стержня в неупругое состояние;
– материал стержня – сталь 3, определяющее уравнение (1) для которого имеет вид [2]:
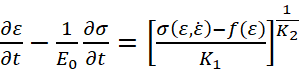, (8)
где
,
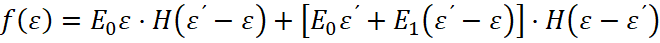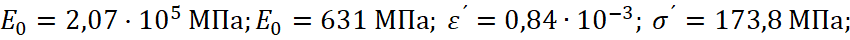
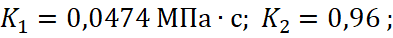
H(ε-ε´) – единичная функция Хевисайда;
ε´ – деформация, соответствующая условному пределу текучести σ´ материала на диаграмме Прандтля, причем справедливо равенство
σ´=E0·ε´.
На рисунке 2 приведены результаты аппроксимации экспериментальных диаграмм динамического нагружения стали 3 (сплошные линии) определяющим уравнением (8) (штриховые линии) [1].
Рис. 1. Схема внешнего нагружения неоднородного трубчатого стержня и принятые обозначения
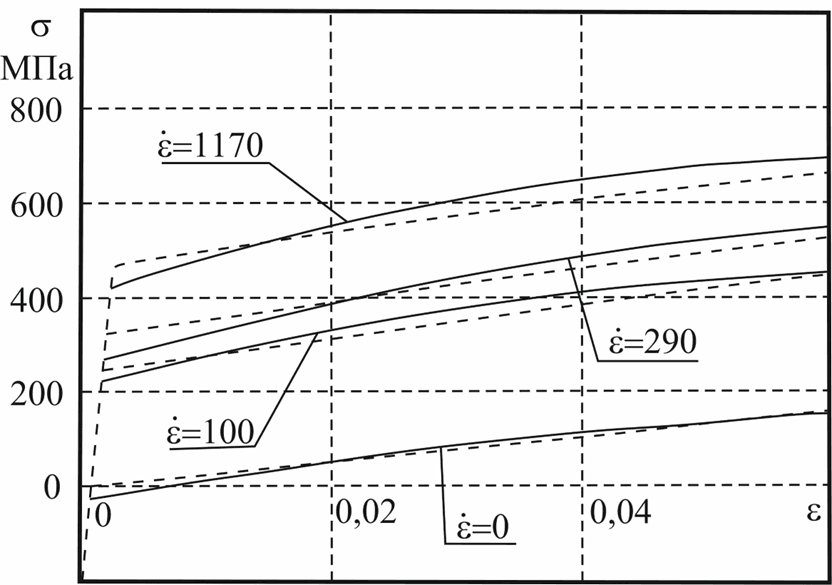
Рис. 2. Аппроксимация диаграмм динамического нагружения для стали 3 конституционным уравнением (8)
Численные значения амплитуд импульсов напряжений на нагружаемом торце стержня принимались незначительно меньше условного предела текучести материала стержня и варьировались дискретно: σ* = 110; 130; 150 МПа, что позволяет на начальном этапе распространения волны рассматривать ее упругой. Причем, если в случае геометрически однородного стержня параметры напряженно-деформированного и кинематического состояния материала в волне в различных сечениях стержня изменяются во времени одинаково, то в случае его геометрической неоднородности параметры упругой волны изменяются. В частности, для описания изменения параметров состояния материала на переднем фронте упругой волны получена система трех обыкновенных дифференциальных уравнения вида:
,
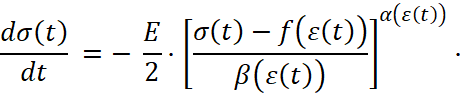
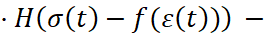
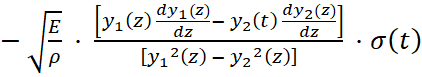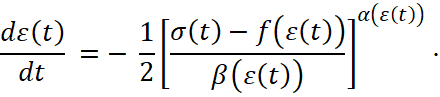
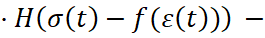
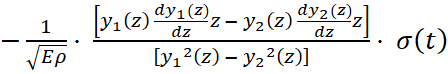, (9)
,
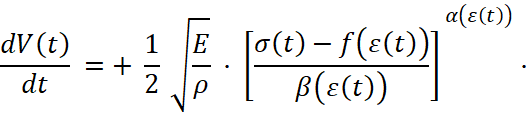
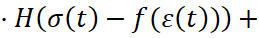
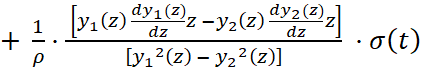при этом в последней системе переменная z, входящая в функции y1(z) и y2(z) и в их первые производные, не является независимой, а связана с единственной независимой переменной t скоростью распространения упругой волны в материале стержня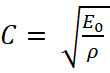 
линейным соотношением
,
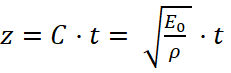где ρ – плотность материала стержня.
Кроме этого, в системе уравнений (9) по отношению к системам (1), (4), (6) изменился аргумент входящих в них функций Хевисайда, что имеет конкретный физический смысл: на переднем фронте волны в силу его мгновенности не успевают развиться неупругие деформации, состояние материала является упругим, и, как следствие, эквивалентом диаграммы статического нагружения является условный предел текучести на билинейной схеме Прандтля.
Длительность импульсов растягивающих напряжений на нагружаемом торце стержня принималась равной времени прохождения передним фронтом волны трети длины стержня:
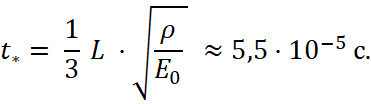
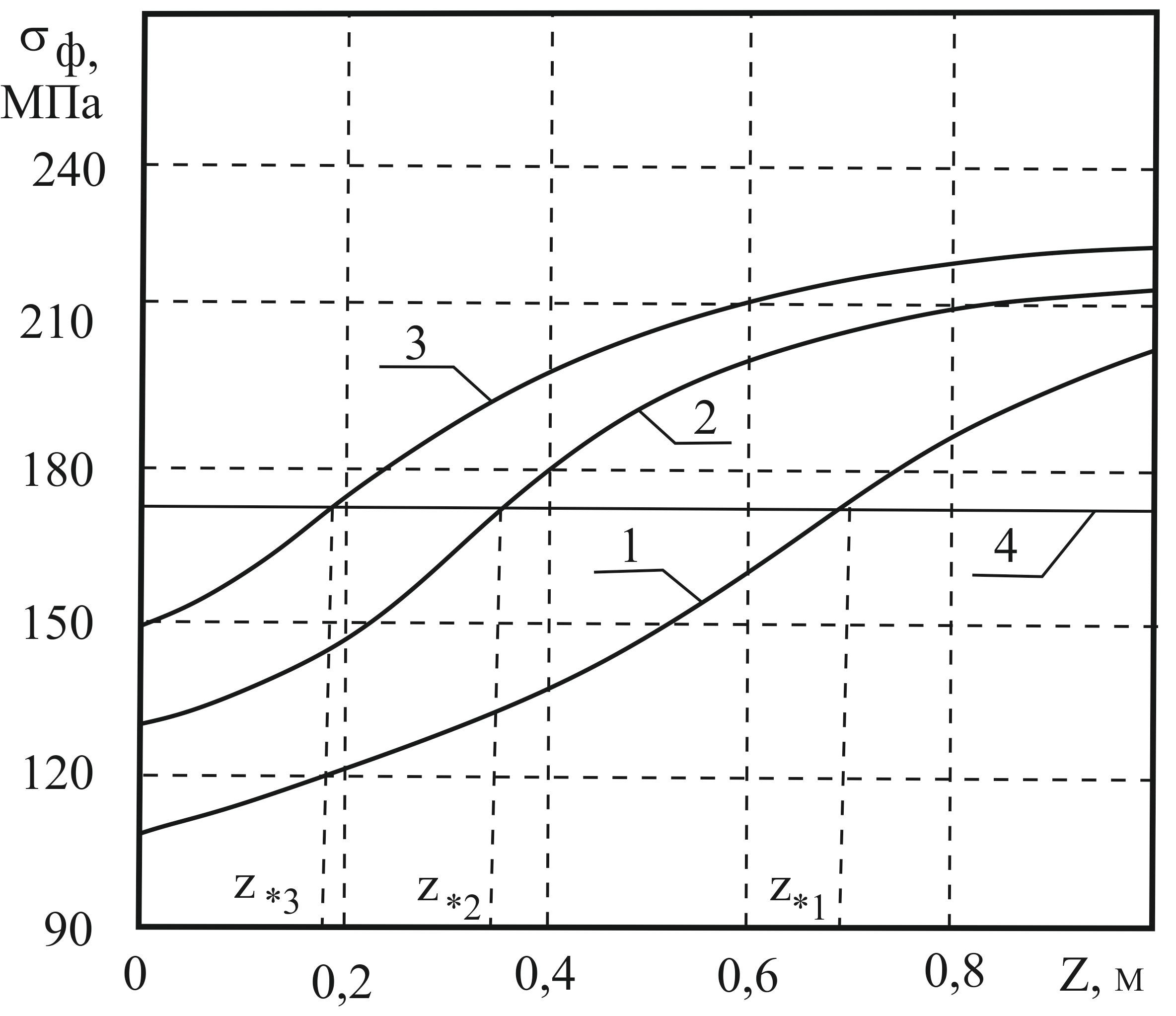
Рис. 3. Изменение напряжений на передних фронтах продольных волн по длине стержня
Некоторые результаты численного решения задачи иллюстрирует рисунок 3, котором представлено изменение напряжений σф на передних фронтах волн по длине стержня для различных амплитудных значений граничных импульсов: кривая 1 – для σ* = 110 МПа; R1=0,10 м; кривая 2 – для σ* =130 МПа; R1=0,15 м; кривая 3 – для σ* = 150 МПа; R1=0,20 м. Во всех случаях наблюдается интересная закономерность: на участках между нагружаемым торцом стержня и точками перехода материала в волнах в неупругое состояние (точками z* пересечения кривых 1, 2, 3 с прямой 4, соответствующей условному пределу текучести материала σ´) интенсивность возрастания напряжений на фронтах волн увеличивается, а после прохождения фронтом точек z* вторые производные функций меняют знаки и соответствующие интенсивности уменьшаются. Это объясняется «срабатыванием» в точках z* единичных функций Хевисайда в правой части первого уравнения системы (9) и включением в решение упруго-вязкопластического компонента конституционного уравнения, причем последний входит в уравнения (9) с отрицательным знаком.
Таким образом, в данной работе численно протестировано решение задач продольного волнового нагружения геометрически неоднородных стержней из упруго-вязкопластических материалов в рамках гипотетического прямоугольного граничного импульса растягивающих напряжений и без учета потенциально возможной деструкции материала. Полученные результаты не противоречат физическим закономерностям процесса и могут быть использованы для решения ряда задач, имеющих прикладное значение.
