1. The principles of interaction of an electron and a proton with the presence of radiation on the base of Lorentz's force and Coulomb's force.
Accordingly, in order to exclude the postulates of Bohr at the prohibition of radiation in discrete orbits, we need to show a way to replenish the electron energy under the condition of thermodynamic equilibrium based on the constants of the propagation medium.
The principle of the formation of motion of electron in orbit can be represented as follows. In the beginning the electron is on distance from a proton in a motionless condition. Then the Coulomb's force acts on the electron: Fкул=еE. In this case, the electron acquires a velocity in the direction of the proton according to the formula:
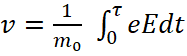(1)
However, when moving at a speed v in the direction of the proton, we get the Lorentz’s force, which is calculated by the formula:
(2)
And this Lorentz’s force is directed orthogonally to the Coulomb’s force. Here we take into account the fact that, according to our theory, we have ε0=u/c; μ0=1/(cu);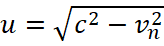 
– a significance is associated with the average integral magnitude of exchange (movement) in contrast system vn. The presence of velocity vn in the contrast system follows from GRT, since the space-time curvature introduced by Einstein relies on SRT at the speed of motion of a moving system relative to a motionless observation system. However, for each smallest element of space and time, which gives a common space-time curvature, this velocity of SRT in GRT of Einstein has not the binding to the so-called absolute observation system, unless we consider the existence of an observation system from the opposite, where the velocity vn characterizes the exchange between two global opposites. At the same time, the absolute system of coordinates is obtained due to the fact that systems of opposites are connected through the speed of light and therefore the speeds used in GRT of Einstein for the smallest space-time elements are always less than the speed of light. In this case, we have the magnitude of the projection of velocity onto significance of time (otherwise, the vector of velocity at projections in spatial view would lead to the presence of ether), and it is this approach that provides an absolute motionless observation system for all the smallest elements of space-time curvature. As it was shown in [1], constants determine the difference of mass between a proton and an electron, based on the thermodynamic equilibrium condition. Accordingly, the SRT and GRT of Einstein establishes the rule according to which the kinetic energy of one opposite is expressed as potential energy of the other opposite, and it gives the difference of mass between a proton and an electron. The Einstein could not solve the problem of the gaps (of the singularities) because he considered the presence of only one system of observation, without taking into account the particle-wave dualism. Also we note that the harmonic oscillator equation served as the basis of quantum mechanics because this equation shows the relationship of potential energy with kinetic energy as systems of opposites, and obeys the equation of a circle, i.e. a closed system. In our theory, the essence of the Lorentz's force actually determines the response in the view of reaction from the system of the opposite on the action which is being associated with a change (with movement) in our observation system. Moreover, this counteraction is directed orthogonally to the action of the Coulomb force, since otherwise there would be a compensation of forces, and movement would be impossible. However, the Lorentz’s force, which counteracts the movement of the electron to the center of the proton nucleus and gives a tangential velocity of movement vτ, also leads to the formation of a force directed into opposite side to the Coulomb’s force in the form of a magnitude Fradlor=е[vτB]. If we do not consider radiation and absorption, then the equilibrium with the movement of the electron along the orbit of the radius Rорб and the tangential velocity vτ will occur when the Coulomb’s force is equal to the Lorentz’s force Fradlor=е[vτB], and they will be directed opposite to each other:
Fкул=Fradlor (3)
It is clear that the presence of any force is associated with the presence of absorption or radiation of kinetic energy; otherwise there simply cannot be changes in the state of the particle. Hence, it would be possible to write the equation of forces in the form:
Fкул=Fradlor+Ftanlor (4)
However, there is no compensation for the force Ftanlor in the formula (4), and this would mean an infinite increase in the energy of the particle if we did not have the radiation reaction force [2] in the form
Fр.изл=2е2/(3c3)d2v/dξ2 (5)
Here we have: ξ=t-Rорб/c. This formula of the reaction force of radiation clearly does not correspond to the classical formula in the mechanics of the occurrence of acceleration and force, since the force is determined not by the first derivative of the velocity onto magnitude of time, but by the second derivative of the velocity onto magnitude of time, that is, of the derivative of acceleration onto magnitude of time. In other words, if the acceleration has a constant amount, then there is no radiation reaction force. This contradicts electrodynamics, where when an electron rotates in an orbit, we have a constant equidistant motion with radiation. With this approach of calculating the radiation reaction force, another paradox arises, if we proceed from the condition that the velocity v is the tangent velocity v=vτ=ωRорб to the radius of orbit. This velocity is a constant magnitude due to the fact that the orbit does not change. And in this case, there is no radiation reaction force in the direction of movement. This would mean that there is no radiation, but according to classical electrodynamics, there is radiation when an electron rotates around a proton, and it is described on the basis of the Hertz dipole. Here, the radiation is associated with a change in the electromagnetic field in the environment when an electron rotates around a proton. At the same time, the paradox is resolved if we assume that the frequency of the radiation of the Hertz dipole in discrete orbits is constant, and the radiation energy is also constant E=ℏω. Indeed, this is exactly what we have in accordance with the equation for the harmonic oscillator, taking into account the quantization of energy:
p2/(2m0)+m0(x2πf)2/2=nhf (6)
However, in this formula, the Coulomb’s force is replaced by a centrifugal force, and such a replacement contradicts the formula:
E=m0ϕ2r2/2+α/r (7)
where the centrifugal force should compensate for the Coulomb’s force. At the same time, it must be remembered that the centrifugal force is associated with the absence of loss of kinetic energy in the previous direction, and this excludes the very change in the state of the particle. That is, we do not have the mechanism of action of the centrifugal force associated with the transfer of energy from anything, but we only have a mathematical formula for calculating this force based on the speed of rotation of an electron in orbit. Therefore, the replacement of the Lorentz’s force in quantum mechanics with the centrifugal force gave an element of the miracle of change in motion of particle.
Further, we note that if the radiation energy has a constant magnitude, then the radiation reaction force is also a constant value. In other words, the braking force for the velocity of electron is associated with radiation energy due to the formation of an alternating electromagnetic field when the electron rotates around the proton. Here, the Coulomb’s force forces electron to change the direction of movement with the loss of energy in the previous direction. In this case, the reaction force of radiation is directed into other side to the direction of the radiation energy. Practically in an electron (when it is reflected through a corpuscular form according to the Dirac equation system), the interacting electronic and muonic neutrinos (antineutrinos) of one direction are replaced by electronic and muonic neutrinos (antineutrinos) of another direction. In this case, the previous electronic and muonic neutrinos (antineutrinos) interact to form an electromagnetic wave that is emitted. We observe the nature of the radiation direction in the Hertz dipole and in synchrotron radiation [3]. It can be assumed that the reaction force of radiation Fр.изл gives the compensation for the Lorentz force Ftanlor, and then we have a general equation of forces:
Fр.изл+Fкул=Fradlor+Ftanlor. (8)
However, it must be remembered that in equation (8), the force Fр.изл refers to classical mechanics with the presence of paradoxes, and the other three forces are determined by electrodynamics.
This means that in the future it is necessary to consider a more acceptable option for the equation of forces, and now we note that the presence of forces corresponds to the representation of energies in the equation of electron motion, taking into account kinetic and potential energy:
E=m0r2/2+m0ϕ2r2/2+α/r (9)
According to the accepted assumption in quantum mechanics, the loss of energy by an electron at presence of radiation should lead to a change in the parameters of the electron with a fall on the nucleus. However, this cannot happen, since we see from (8) that the equality of forces is observed at a certain magnitude v, and besides, the significances е, c, m0 are constants in the electron - proton system. The magnitudes of E, H are also determined by the magnitude of the charged particle of proton and depend only on the length of the radius of the orbit Rорб, which, as well as the magnitude v=ωRорб, is obtained from the condition of the equation of forces (8). The proton is practically motionless, and it means proton has no changes. At the same time, we remember that the frequency of radiation ω, and hence the radiated energy, does not change, that is, we have a discrete spectrum of radiation. So, to change the state of velocity and orbit, you need to have a variable parameter in the equation of forces, and only the parameters of the medium in the form ε0=u/c and μ0=1/(cu) are such parameters. Accordingly, only the significance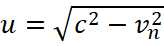 
associated with the velocity in contrast system can, as it were, be responsible for the energy consumption of radiation. Indeed, if we have the more kinetic energy in the opposite system (and it is uniquely related to radiation), then the higher the average integral magnitude vn. Hence, the magnitude u becomes smaller and the significance μ0 increases, and hence the magnetic field strength B and the Lorentz force have the increasing too, but the Coulomb force has the decreasing. This leads to the transition of the electron to a higher orbit already in our observation system. An increase in the radius of the orbit leads to an increase in the velocity of the electron in orbit. However, we have a connection of kinetic energies through velocities in opposites according to the circle formula 
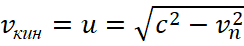. Otherwise, we will not have a closed exchange and this is equivalent to miracles and the absence of the laws of physics. Practically kinetic energy is associated with the Louis de Broglie wave. Therefore, an increase in speed in one opposite leads to its decrease in the other opposite. It should be noted here that the magnitude of u refers to the reflection of the potential energy of the spatial-temporal curvature of the environment, but the magnitude of vкин determines the analogue in averaging the kinetic energy of objects of other opposite. This means that there must be a thermodynamic equilibrium of opposites, which actually obeys Planck's formula. In this case, radiation in one system means absorption in the other opposite, and vice versa, as a result of which a radiation spectrum is formed with the corresponding difference of mass between a proton and an electron in accordance with the thermodynamic equilibrium condition. And this difference of mass in the dynamics of interaction through radiation in each of the opposites is a constant magnitude. And this suggests that the kinetic energy of the radiation of one opposite system forms the potential energy in the other opposite, and vice versa. Hence, there are no conditions for changing the parameters and obtaining conditions for the electron to fall on the nucleus due to a closed exchange between opposites. Thus, the paradox of the electron falling on the nucleus due to radiation is solved on the basis of a closed interaction of opposites. Actually, physicists intuitively came to a closed system based on the use of an electromagnetic vacuum with equal absorption and the radiation of energy based on the Einstein coefficients and the involvement of the Planck formula, but the mechanism of replenishment at the same time had no justification, since it was associated with probabilities. Hence the erroneous conclusions went further, so it should be noted that the inflationary theory adopted in current physics is based precisely on the fact that electromagnetic radiation seems to be lost in infinity, and therefore, according to the assumption of physicists, all this should end in complete decay with transformation into zero. It is clear that this approach also contradicts the presence of such a constant as Planck's constant in the view of the minimum magnitude of the universe, taking into account the constant thin structure and the speed of light. This approach was the fact that the classical Maxwell equations did not obey the Lorentz-Minkowski transformations, which means they could not give a closed exchange between opposites, but our theory corrected this error.
It should be noted that radiation in discrete orbits is equal to absorption as a result of thermodynamic equilibrium and this radiation is called relict radiation, although, in fact, it has nothing to do with the Big Bang. Therefore, the observed radiation spectrum is determined precisely due to the transition of electrons from orbit to another orbit, since in this case it is possible to obtain an excess over the level of the noise associated with thermodynamic equilibrium. It is this linear form of the spectrum components that is observed in experiments. Thus, we have obtained result of the replenishment of the orbital velocity of motion in the presence of radiation, and it occurs due to the Lorentz force, which the Bohr did not take into account, since he did not understand the role of such constants of the universe as electric and magnetic permeability, which are constants precisely due to the dynamics of the interaction of opposites through radiation and absorption. However, the Bohr undoubtedly took a step forward in describing orbital motion, as he presented kinetic energy through potential energy, which made it possible to calculate the radii of orbits and the energy of transition from one state to another state. Now we have to clarify the equation of equality of forces (8) based on the equations of electrodynamics with the exception of paradoxes. Indeed, the formula (8) does not reflect real elementary objects, and any change in the state of an object, which is interpreted as the action of forces, is associated either with the absorption or radiation of elementary small objects.
2. The connection of forces of influence on electron with the equations of electronic and muonic neutrinos (antineutrinos).
Since the forces of action on a corpuscular particle are determined by a change in its state, and this is due to the radiation and absorption of elementary objects of the universe, then it is not possible to determine the presence of an impact in any other way, as there will be no changes in the object. Hence, the impact of forces must always be expressed through real elementary objects through absorption and radiation.
Previously, we received a mathematical description of these elementary objects based on the well-known practical Faraday's law (the Bio-Savard law is an analogue from the system of opposite), and it is impossible to imagine any object of the universe outside the interaction of these simplest objects due to the fact that otherwise there will be a break (gap) from simple to the complex representation. Accordingly, we have also shown how the interaction of these simplest objects, which are called electronic and muonic neutrinos (antineutrinos) gives electromagnetic waves [4] and corpuscular particles. At the same time, we have shown that the corpuscular motion of particles is determined by a system of Dirac equations through electronic and muonic neutrinos and antineutrinos [1]. In this case, the direction of motion of the particle is determined by the magnitudes in the arguments of functions of these electronic and muonic neutrinos and antineutrinos. Accordingly, the vector of velocity will be determined by the composition of absorbed and of emitted electronic and muonic neutrinos and antineutrinos. It is clear that the impacted forces should be determined precisely by the composition of these electronic and muonic neutrinos and antineutrinos, which means that it is necessary to show how the impacted forces are related to the components of electronic and muonic neutrinos and antineutrinos. In addition, it must be shown that the physics of interaction itself is associated with changes in opposites on the base of SRT and Einstein's GRT, which determine the closed system of exchange and the presence of laws themselves.
Indeed, the improved differential equation of Maxwell in projections of coordinates and time has the view [4]:
(10)
Here i=(-1)1/2 – imaginary unit. Next, the left part of the equation is being represented as a dependence on the differential of one variable, taking into account that the magnitude of the differential ∂z in accordance with [5] can be displayed as ∂z=ic∂t. In fact, the law of connection of opposites was intuitively introduced into quantum mechanics in the form |1|=|i| that excludes the appearance of an arithmetic zero in the Universe, i.e. we have excluding of zeroing of quantities due to the fact that a change in one quantity means an automatic transition to the system of opposite with the assignment of an attribute of belonging (i), and a change in summation to subtraction through the factor of action from laws, without which equality in quantity cannot be obtained.
At the same time, it should be noted that in physics, unlike mathematics, there is no such operation as squaring, since changes are always associated with a transition to the opposite. If there were such a transition, it would be impossible to observe it, because there are no changes in the opposites. And in each of the opposites there is the presence of the same finite quantity, which is associated with the presence of such constants as Planck's constant and the speed of light. Otherwise, it would be necessary to assume the existence of a miracle with the appearance of objects from nothing and the disappearance of objects into zero with the absence of the need for the laws of physics with preserving of quantity. Hence, as an attribute of belonging to opposites, the unit will turn into an imaginary unit, and the imaginary unit will turn into a minus unit, characterizing the reaction to the action. In other words, this means that integration and differentiation characterize the transition to the system of opposite with multiplication by an imaginary unit. That is, when considering the interaction between opposites in mathematics, when integrating and differentiating, it is necessary to introduce multiplication or dividing by an imaginary unit (otherwise you will not get a change in laws). Recall that the attribute of the imaginary unit was introduced because the transition must counteract the primary change (the law of action and counteraction), otherwise there would be a miracle of increasing to infinity. The speed of light (changes) also determines the difference of opposites, in the sense that for the connection of opposites there must be a mutual transition (otherwise complete independence and existence of opposites for each other is absent), and a change in one magnitude in a closed system gives the opposite magnitude, since there is no other representation. Hence the meaning of equality ∂z=ic∂t is that opposites are connected through the speed of light (the velocity of exchange) and counteract each other. The significance of the projection on magnitude of time – Bt refers to the system of opposite. Therefore, the significance of z must be brought to the opposite, i.e. expressed in terms of a time equivalent and we obtain an equation of the form:
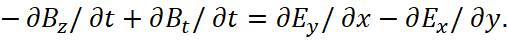(11)
Differentials in practice can be replaced by increments Δ, as there are no infinitesimal quantities in the Universe (this contradicts Planck's constant), then we rewrite:
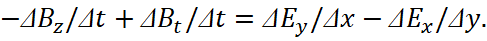(12)
Next, according to the rules of mathematics, we multiply the members of the equation by Δх, and we get:
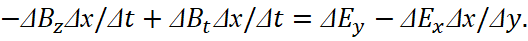(13)
First, let's consider the variant of implementation of the actions at the propagation of an electronic or muonic neutrino (antineutrino) without changing the environment on the base of SRT of Einstein in our observation system. In this case, the simplest object has propagation at the speed of light and all coordinates in environment are related to time in the similar way, that is, Δх/Δt=с and Δх/Δy=1. Then, in the case of an isotropic space, we will have the equation:
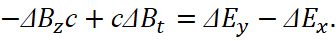(14)
This equation determines the equality of the strengths during the propagation of an electronic or muonic neutrino (antineutrino) at the speed of light. Next, we will write down the significance of magnetic induction, taking into account the fact that the magnetic permeability constant is determined by the motion in the contrast system:
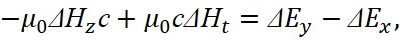
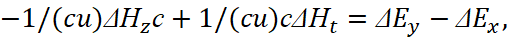(15)
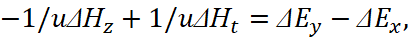
Further, we take into account that the equality of members in a closed cycle determines the propagation of electronic and muonic neutrinos (antineutrinos) without external interference, and hence, taking into account the closed system and for u = (c2-vпр2)1/2, we have:
.
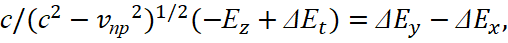
(16)
In fact, we get that the last two equations are defined as fulfilling the Einstein's SRT condition in the system of opposite for space and time in accordance with formulas:
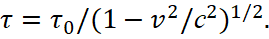(17)
Actually, this means that the result of the appearance of electronic and muonic neutrinos (antineutrinos) in our observation system is the presence of corpuscular motion with a space-time curvature in contrast system in accordance with Einstein's SRT. If we take into account the closure on the system of opposite, then we can get, for example:
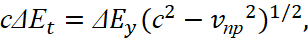
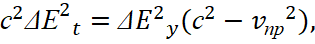
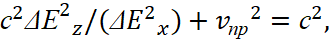
(18)
The fourth formula in (18) characterizes the movement of the response in our system (due to the heterogeneity of the intensities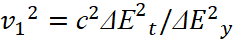 
), to the movement in the system of opposite according to the equation of a circle - a closed system. Consequently, the result of the presence of the magnitude – vпр is the appearance in contrast system of inhomogeneity (discontinuities) in the intensity of fields over the coordinates, which in this case characterize the space-time curvature. Indeed, when vпр =0, we have ΔЕz=ΔEx, ΔЕt=ΔEy. Actually, if vпр is not zero, then this gives rise to electronic and muonic neutrinos (antineutrinos), which connect these gaps. Now let's complicate the task and consider the variant when there are objects in our system that obeys Einstein's SRT with motion. At the same time, we assume that Δх/Δt=vx, and Δх/Δy=1 (there is no motion between x and y), then in the case of charge of particle with q =e = ±1 (there simply cannot be any other meaning for the simplest objects, since the Einstein energy equation will not be fulfilled), we will have the Lorentz total force equation:
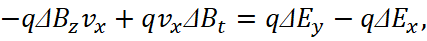
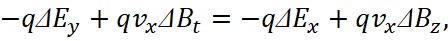(19) 
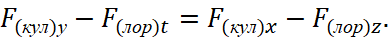
It should be noted that the transition from Coulomb and Lorentz forces to electromagnetic components (we did this in reverse order) was also made in electrodynamics when trying to describe the pressure of light, and it will be shown further.
However, in this case, the form without projection on significance of time was taken into account, that is, the error of describing electromagnetic fields according to the Faraday's equation was preserved, with the corresponding paradox of the absence of subordination to Lorentz-Minkowski transformations with the presence of projection on significance of time and violation of the law of conservation of quantity in the form F(кул)у=F(кул)x-F(лор)z. As a result, we have an inequality of forces in opposites, which correspond to the lack of compensation. Further, we note that in our theory, the counteraction to the magnitude of the change in motion along the x coordinate, under the action of a force in one opposite qΔEx, turns out to be a magnitude qvxΔBt, that is, the counteraction is determined through an orthogonal component onto significance of time from the other opposite, taking into account speed vx. Accordingly, the occurrence of force qΔEy, in turn, is compensated by the presence of force from magnitude -qΔBzvx, and this ensures compliance with the law of conservation of quantity. Therefore, the intensity of electromagnetic fields characterizes all possible force actions due to the fact that the exchange takes place through them, and this, by the way, is what Feynman tried to display through Lorentz transformations of electro-magnetic fields [6]. However, he did not take into account the presence of a common space-time and electromagnetic continuum, which is obtained by taking into account the projection of electric and magnetic fields onto significance of time. Thus, we get that every force action occurs on the basis of the simplest objects of the universe, which are electronic and muonic neutrinos (antineutrinos). At the same time, in the form of the record (19), we consider the values of the electric and magnetic field strengths in the form of a force action on the coordinates of four dimensions on an object in the form of a particle with a charge q = ± 1 moving at a speed vx. In other words, we consider the action of an electronic or muonic neutrino (antineutrino) on an object that has motion (change), with velocity vx. Next, we will write the equation (19) taking into account the movement in the opposite direction:
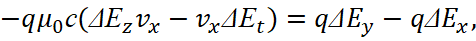
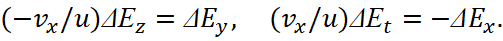(20)
It is clear that using the third equality in the equations (20), we focused on the physics of the formation of the Lorentz force for a moving elementary particle. The fourth equality in the equations (20) is obtained by the principle of the presence of the remainder. Actually, according to our theory, the fourth equation should also characterize the motion of a particle with subordination to the Lorentz force, but in contrast system, with the compensation of the Coulomb force along the x axis in our observation system, since the projection onto significance of time in one opposite turns into a projection along the length in the other opposite and the movement along the x coordinate becomes a movement along the y coordinate. Further, on the base of the magnitude u =(c2-vпр2)1/2 with squaring of the members of the equation, we have:
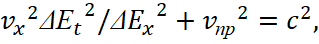
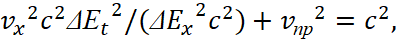(21)
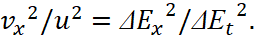
Accordingly, it can be represented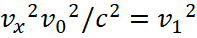 
, then the values vx and v0 are inversely related. Thus, unlike formula (18), in the interaction of electronic and muonic neutrinos (antineutrinos) with space-time curvature, which has the appearance from changes associated with the velocity vx in our observation system, we get a change in the intensity of electromagnetic fields at the same time from the velocity vx and velocity u in contrast to the absolute system moving at the speed of light. And this means, under the condition of the closure of the universe into two global opposites according to the equation of the circle, there is a change in the dynamics of the components in the interacting objects, and this is reflected both in the energy characteristics of these objects and in the direction of movement. In addition, given the fact that the universe, in accordance with the division into two global opposites and with the presence of a dependent and independent part of each opposite, has 4 coordinates in space and time, the field strengths can be interpreted in the view of the velocity of change in the corresponding observation system, and of these systems of observation are also four. This is also due to the fact that otherwise it would mean independence from space and time. The last formula in (21) can also be represented as a relation of length and time according to Einstein's SRT in the private case, at considering closed processes (invariance) from two observation systems (from mobile and motionless), then in cause vпр=vx and at the analogic dimension in projections ΔЕt=t, ΔЕx=x/c we have:
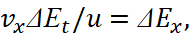
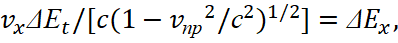(22)
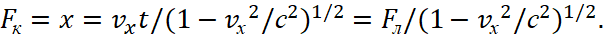
In fact, we have result that with an observation system from a motionless absolute system with the movement of an object and with the subordination of the Einstein SRT, in system of opposite, this will be expressed in a change in dimension in magnitude x, and changing of magnitude of x can be characterized in the appearance of the Coulomb’s force Fк due to inhomogeneity in accordance with the GRT of Einstein.
At the same time, the Lorentz force Fл can be interpreted as an analogue of the magnitude vxt, Indeed, according to the formula (22) in the right side from the sign of equality, we have a closed continuity equation -∂Bz/∂t+∂Bt/∂t and the corresponding time magnitude t in the opposite observation system turns into the significance of magnetic induction Bz. In fact, such a connection between the Coulomb force and the Lorentz force with the fulfillment of Einstein's SRT was previously obtained by the scientists before us when describing the electromagnetic continuum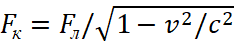 
.
In essence, this means fulfillment of the law of conservation of quantity, and in the variant of considering processes based on the interaction of two global opposites, and in the variant of considering the interaction within one global opposite for an object, when kinetic energy is converted into potential energy of space-time curvature. The only difference is that at taking into account the interaction of two global opposites, we took the kinetic energy for the space-time curvature of not one object but the kinetic energy of interaction from all objects, and it gives the constants of electric and magnetic permeability in contrast system of observation. Actually, if the general space-time curvature were not taken into account, then we would have a complete closure of the object in the interaction of opposites, and then such an object would be impossible to detect.
The presence of the Lorentz’s force is determined by the fact that the reaction is not connected with the zeroing of the force of action through the force of reaction, as is customary according to Newton's third law, but with the transition from rectilinear motion to closed movement around the circle, which excludes the disappearance of objects from the universe. It is clear that at a certain magnitude, equality of forces will occur, and we will get an orbital closed motion. In this case, the radius of the orbit will be determined by the constants of electric and magnetic permeability. That's why we determined the radius of the Bohr orbits taking into account the constants of electric and magnetic permeability according to formula [7]:
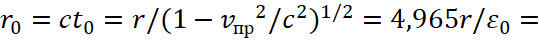
(23)
and this was not taken into account by the Bohr according to formula:
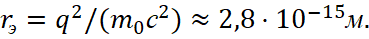(24)
Thus, all processes in the universe are described on the basis of quantitative representation and changes in these quantitative significances in the system of two global opposites.
Hence we have the conclusion that all forces acting on the objects of the universe, including the Lorentz’s force, are directly related to the fulfillment of the condition of the closure of the universe into two global opposites in accordance with the changes in these opposites expressed in terms of the velocity of change, and it is also reflected in SRT and GRT of Einstein. At the same time, we see that the space-time curvature in both opposites affects the magnitudes of the electromagnetic components, and it leads to a change in the direction of movement and such approach provides the closed solutions of the presence of corpuscular particles. In other words, there is a reason for closed process and for the transition from moving at the speed of light to moving at speeds much less than the speed of light. In addition, it should be noted that the presence of any forces is associated with changes (movement) in opposites, that is, the Coulomb’s force, which is recognized as static, is actually associated with changes (movement) in the opposites through the emitted and absorption energy of elementary particles.
Accordingly, it is necessary to understand: "Why physicists could not to make this conclusion before us?" To this purpose, we will consider the role of the Lorentz’s force in the formation of the idea of the existence of a common electromagnetic continuum, and what paradoxes arose among scientists due to the refusal to consider processes in two global opposites.
3. The connection of forces of Coulomb and Lorentz at the description of the electromagnetic continuum.
The first attempts to establish the connection of electromagnetic forces with space-time curvature (although without the principle of converting one significance into another significance, and vice versa), were made on the basis of proving of common electromagnetic continuum and space-time continuum by converting the Lorentz’s force into the Coulomb’s force on the base of the Lorentz equations in accordance with Einstein's SRT. At the same time, the presence of an electromagnetic continuum is based on the transformation of electric forces into magnetic ones due to the speed of motion with the subordination of the Einstein SRT. In other words, the independence of electromagnetic forces from the system of coordinates is virtually excluded. Hence, R. Feynman writes [8]: "Magnetism and electricity are not independent things, they should always be taken together as one complete electromagnetic field. Although in the static case Maxwell's equations are divided in the view of two separate pairs: one pair for electricity and other pair for magnetism, with no apparent connection between both fields, nevertheless, in nature itself there is a very deep relationship between them arising from the principle of relativity." Consequently, R. Feynman was faced with the task of showing how the Coulomb’s force
Fк=qE (25)
is related to the Lorentz force, taking into account SRT of Einstein. More precisely, with the part of force that interprets the dependence on magnetic forces:
Fл0=q[v0B]. (26)
Here q is the charge, v0 is the velocity vector of the charged particle, E and B are, respectively, the vectors of the electric field and magnetic field of induction. The complexity of the problem is that in the presence of an electric and magnetic field, the force acting on a moving of charged particle is equal to the sum [9]:
. (27)
In other words, in this case, the moving particle is affected by two forces. At the same time, physicists believe that since the magnetic force is always directed perpendicular to the velocity of the charged particle, then this force does not work on the particle with energy consumption. However, this is not the case, as we can be seen from figure 1.
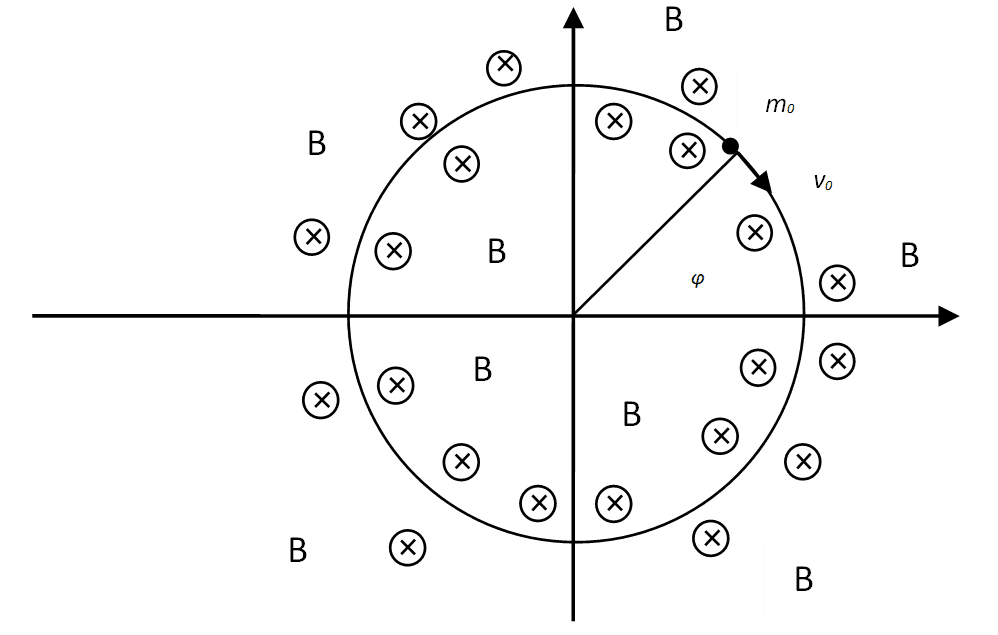
Fig. 1. Motion of a charged particle along a circle under the influence of a magnetic field
Indeed, if an initially charged particle ('electron) has a velocity v0, then, in the presence of an opposite charged particle (proton) in the center and with a magnetic field, electron moves along a circle. However, if the particle did not lose kinetic energy in the direction of motion, then in this case the movement would be in a spiral with going to infinity. Accordingly, the kinetic energy would reach more and more magnitude. Therefore, during orbital motion, there is a loss of energy in the rectilinear direction, and energy is added in the perpendicular direction. And the change of energy in the direction does not occur without doing work. By the way, this would exclude the representation of the Lorentz force as an opposing force relative to the Coulomb force.
In fact, the exclusion of performing of work in closed motion is equivalent to violating the law of thermodynamics with the Carnot cycle and means the presence of a perpetual motion machine. We note that unlike Newton's formula according to his third law (regarding the force of action and reaction as a factor of zeroing forces), we cannot have zeroing, since this means turning into zero (in this case, the opposites would simply disappear). It is clear that in a circular motion, the loss of energy in the previous direction of motion will be accompanied by the emission of this energy (there is no other way to lose kinetic energy even in the same vacuum). In other words, the accelerated motion of a particle along a circle is inevitably accompanied by radiation, but since the direction of motion changes to orthogonal, we get an increase in kinetic energy in a new direction under the influence of a magnetic field. Due to the fact that the total energy of the particle has not changed, but the direction has changed, physicists have made the wrong conclusion about the absent of work on the particle, although it is possible to change the direction only by decreasing one magnitude and adding another magnitude, and this is radiation and absorption.
In fact, this means the solving of the paradox associated with the loss by electron of radiated energy when electron has rotating around a proton. We have replenishment through a magnetic field.
It becomes clear that in this case, due to the loss of energy, the magnetic field, which is characterized by the magnitude of magnetic induction B, would have to weaken, in the absence of ways to replenish this energy. How the energy of the magnetic field is replenished, we have shown above and this is due to the presence of motion in system of opposite with similar radiation. And now, let's consider the method of the relationship between the Coulomb’s force and the Lorentz’s force, which was proposed by physicists on the basis of two similar (positive) charges q1 and q2 with motion along parallel lines with the same velocity v0, at q1 = q2 = q (fig. 2). In this case, at v0<<c, the electric field practically does not differ from the field of motionless charges in the observation system R.
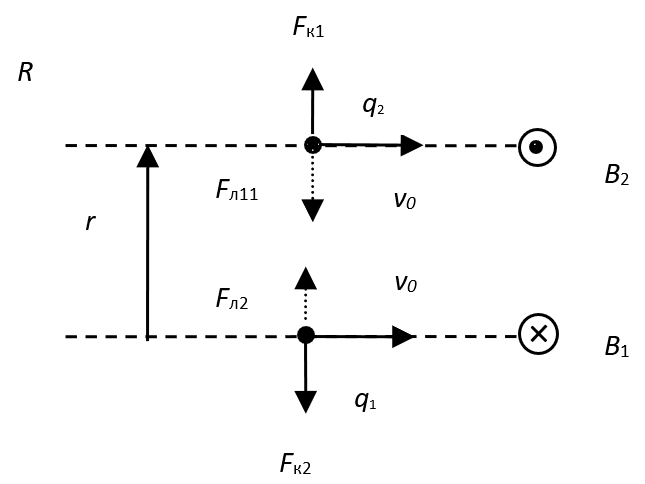
Fig. 2. A variant of the interaction of two moving charges of the similar name
Here we do not consider the option of how we get the movement of charged particles with speed v0. At the same time, in a motionless system R, the magnitude of the external magnetic field can also be expressed in significances of the velocity of the charged particle, and then the magnetic field can be represented as:
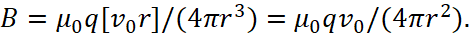(28)
If we return to fig. 1 (when the charged particle has moving in a magnetic field along a circle), then considering the fact that the magnitude of charged particle is a constant significance (according to Dirac's theory, q = ± 1, because there is no energy in Einstein's energy formula for an electric charge), and with a constant magnitude of v0 = const and r= const, the replenishment of the magnetic field energy can occur only through the magnitude μ0. As this result turns out, we have shown above in section 1. Accordingly, proceeding from the formula (28), Lorentz's force will be in the form of significance:
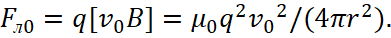(29)
Force of Coulomb looks like:
(30)
Accordingly a parity of force of Lorentz to force of Coulomb we shall reflect in the form of:
(31)
In fact, we have obtained a ratio of forces similar to the last formula in (18), with v0=u.
That is, such a difference between the force of Lorentz and force of Coulomb in the R system is equivalent to the formation in contrast system, on the basis of discontinuities in space and time due to the motion with v0, of electronic and muonic neutrinos (antineutrinos) propagating at the speed of light to connect the discontinuities, and in which the values of these forces are expressed in terms of the energy of magnetic and electric components in the form of field strengths. Thus, any corpuscular motion (and this is always a change of condition) in one system has forming a wave motion in the other opposite system in equivalent quantitative ratios. On the base of formulas (29) and (30), we have no idea how the electric static Coulomb’s force is obtained, and the Lorentz’s force is practically expressed through the Coulomb’s force at replacement μ0=1/(c2ε0) and will be determined in the R system only if there is a movement of charged particles with a velocity of v0. In fact, the magnetic force associated with magnetic induction here is expressed in terms of electric static force, and is added only because of movement. The counteraction according to fig. 2. is reflected through the opposite direction of forces. Only thanks to our theory with the presence of opposites that are connected through the speed of light, the static conditions in one opposite, with the corresponding space-time curvature, is being considered as movement in the other opposite, and then the static Coulomb’s force is the result of changes in the system of opposite and this, by the way, ensures the equivalence of electric and magnetic forces. Hence, the Lorentz’s force, taking into account the formula (18), is the Coulomb’s force, but in the opposite. Physicists obtained the ratio (31) under the assumption that v0 <<c, however, this ratio turns out to be valid for any v0, if we consider the free movement of charged particles without taking into account the changes introduced by the interaction. But in this case, the presence of the Lorentz’s force is not invariant, because there is a system of observation (for example, in the system of observation of moving charged particle R*) with respect to which the Lorentz’s force and the magnetic field are zero (fig. 3).
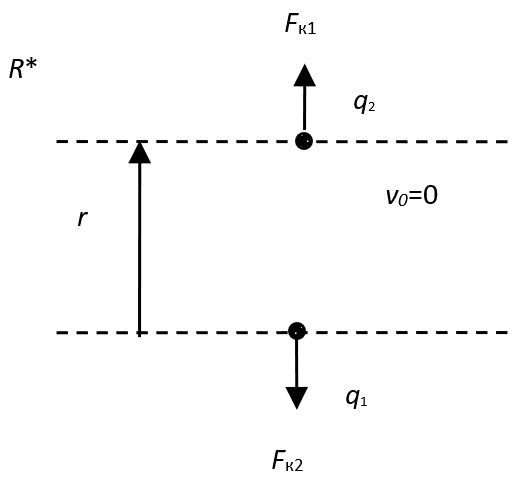
Fig. 3. Interaction in the system of coordinates of moving charged particles
From the formula (31) it can be seen that the ratio of the Lorentz and Coulomb forces is determined only by the magnitude of the velocity of motion. But the mistake here is that both the magnetic induction and the Lorentz’s force were calculated on the base of the same law related to the speed of motion. In this case, we have a paradox which is being associated with the fact that in the system R there is a counteraction to the Coulomb’s force due to the Lorentz’s force, but in the system R*, there are no such counteraction forces. Such a difference of forces, respectively, means the dependence of the laws of interaction from the system of coordinates, which excludes the closed invariance system in any system in accordance of Einstein's SRT.
The reality is that electric and magnetic forces, as opposites, are connected through the speed of light H = cE, that is, in the formula (31) – there are no opposites. Therefore, if v0=с, and this is true for the electromagnetic wave variant, and here the electric and magnetic forces reflect opposites, the Lorentz’s force (magnetic force) is equal to the Coulomb’s force (electric force), and then there are no contradictions associated with invariance due to v0, since the speed of light in any coordinate system is equal to the speed of light. It is clear that the interpretation of the force effect of the Lorentz’s force from the speed of motion in the view of a derivative of the Coulomb’s force means a violation of the laws of physics, since we have different movement of the object under the influence of forces, depending on the chosen system of coordinates. Therefore, in order to eliminate the paradox, the scientists concluded that, depending on the system of observation and the speed of movement, magnetic forces are converted into electrical forces, and, conversely, by analogy, communications in SRT of Einstein. As it was shown above in section 2, the magnetic and electric forces do have a mutual transformation from the speed of motion, by analogy with length and time, but this is related to the speed of motion in contrast system, and this velocity is being expressed in terms of constants of electric and magnetic permeability in our system of observation, taking into account the presence of an absolute system of coordinates associated with the speed of light. However, we are now considering the logic of obtaining an electromagnetic continuum on the base of the conclusions shown by physicists in order to determine their misconceptions. Therefore, we note that for the considered variant in fig. 2, in order to obtain compensation for the effect of the force of Lorentz through electrical forces, it is necessary that the electric forces in the R* system have a smaller magnitude than in the R system. In principle, this means that since the total significance of charged particles characterizing the electric field is a constant magnitude for any particle and according to Dirac theory q = ±1, then the density of electric force lines should change in accordance with SRT and GRT of Einstein. In this case, when moving in the system R, the electric field will has concentration in orthogonal plan with perpendicular to the motion of the particle and this concentration compensates at the change in the magnetic field with the Lorentz’s force based on the inversely proportional relationship of opposites.
Actually, since such a change corresponds to a change in the space-time curvature, and the characters of the field strengths are the constants of electric and magnetic permeability, it only remains to assume that the constants of electric and magnetic permeability characterize the space-time curvature in accordance with SRT and GRT of Einstein. Indeed, a change in the direction of motion of an electromagnetic wave depending on the space-time curvature has been detected in practice and justifies a change in the electric field strength in the direction of movement of an object with a concentration in a orthogonal plan with perpendicular to the direction of movement (fig. 4).
Fig. 4. Change in the density of electric lines of force depending on the speed of movement along the Einstein's SRT
And this is possible only in one case, if there must be an interaction between the space-time curvature and the electrical components, and this interaction is carried out through exchange with mutual transformation. Otherwise, we have complete independence, and then it would be impossible to detect electric forces in space and time.
Considering that SRT and GRT of Einstein reflect a common space-time continuum (this is represented through the Lorentz-Minkowski transformations), it follows that electric forces must have, in addition to projections along coordinates, also a projection along time, because only in this case they will obey the Lorentz-Minkowski transformations. If we take into account that the electric field strength is uniquely related to the magnetic field strength in accordance with the formula H = cE, then the magnetic component should have the same projection along a time. Since, earlier there was no projection of electromagnetic components along time in the classical Maxwell equations, Feynman used vector potentials to prove the subordination of electromagnetic components to Lorentz's transformations. In other words, to solve the problem of the relationship between electromagnetic and gravitational forces, scientists were forced to use the so-called auxiliary functions, which they called vector potentials, in which the much-needed projection of the components along time began to be present. From vector potentials, they carried out an unambiguous transition to electromagnetic quantities. But this actually meant that the electromagnetic components also then had to have a projection along time due to an unambiguous connection. However, physicists could not abandon the classical form of Maxwell's equations, although the unambiguous connection of these auxiliary functions and electromagnetic components left no other option, and it we showed in [4]. Practically, the use of vector potentials means the introduction of another opposite system of observation from the opposite, taking into account that summation in one system is subtraction in the other system of opposite.
It should be noted, the R. Feynman could not refuse from the classical Maxwell equations, he was only in step from creation of the improved Maxwell equations, because introduced projection along time for vector potentials. In accordance with this error, he remarks [10]: "You may think that each vector has something that gives the complements to dimension for 4 vectors in coordinates, so that, for example, a certain magnitude can be associated with vector E, which will make this significance in the view 4 vector along length and time. The same applies to B. Alas, this is not the case. Everything turns out to be completely otherwise from what one would expect".
He did not understand that the absence of a projection along time means that there is only Euclidean geometry with the independence of orthogonal components, and then the interaction of electric and magnetic components according to Faraday's law is in principle impossible. However, at the same time, he tried to connect the electric and magnetic components through Lorentz’s transformations (and this negates the geometry of Euclid) based on vector potentials.
But, here, Feynman did not do without fitting to the result, and for this purpose, as it were, simplified the calculations by taking the significance of the speed of light c = 1. To understand what the fitting to the result is, let's consider this proof, but we take into account the real magnitude in the speed of light, which is not equal to one. For ϕ=At, Feynman used the notation of equations in private differential derivatives in the form:
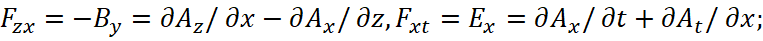
(32)
It is taken into account here that in the four-dimensional representation of gradients, the derivative along time t goes with a opposite sign with the derivatives in x, y and z. In this case, Fμν=-Fνμ, and Fμμ=0. Having received a record of the components in the specified form, Feynman tries to associate these components with Lorentz’s transformations. For this purpose, he is considering some quadratic form:
(33)
In this case, the components Rμ and Sν have the form obeying the Lorentz’s transformations:
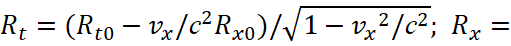
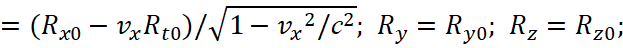
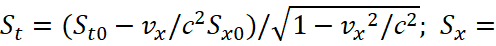
(34)
Let's transform the components of Gμν; we start with Gtx:
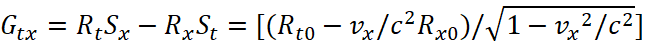
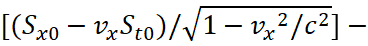
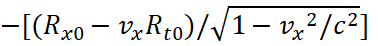
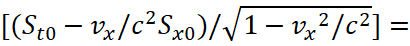
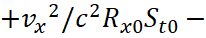
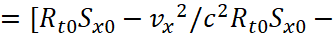
(35)
In other words, we have obtained an invariant relation that does not depend on the system of observation. Let's take another component:
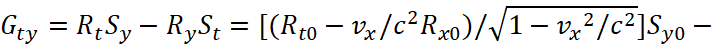
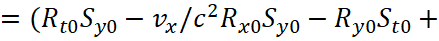
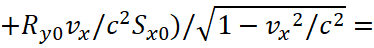
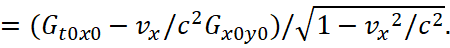(36)
Similarly, we find:
(37)
The next step is to replace magnitude of Gμν by magnitude Fμν. But here it is implied that the components Rμ and Sv should be replaced by increments of components of the form ∂y, ∂t and ∂Ax, ∂At. However, if the component ∂y, ∂t are analogous to the components Rμ, Sv, and are characterized through space-time curvature with subordination to Lorentz’s transformations, then the components ∂Ax∂At, characterize the opposites in the form of an electromagnetic field, which we have shown in [4], through the transition of vector potentials to the improved Maxwell equations. In other words, the practically indicated replacement of Gμν by Fμν means the representation of components of the form ∂Ax, ∂At in the form of objects of space-time curvature with subordination to Lorentz’s transformations.
Thus, Feynman makes an unsubstantiated replacement of the components of Fμν by the real significances of the electromagnetic field, taking into account Fμν=-Fνμ, Fμμ=0, and this leads to the paradoxes shown somewhat below. Next a table of transformation is compiled for all members with the same formal unsubstantiated substitution:
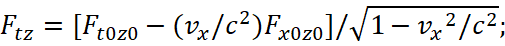
(38)
As a result it is received:
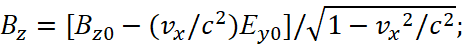
(39)
Here you can immediately see the duality of the representation of electromagnetic components as elements of length and time. Indeed, the transformations of components E and B have a symmetrical form (this, by the way, will be used later in classical electrodynamics to obtain a curvature of the electric field strength depending on the velocity), but, as is known В=μ0Н=μ0сЕ. In this case, it is necessary to assume that μ0=1/c. Hence, we actually have two observation systems relative to E and B. Moreover, the difference is only in the relativity of the observation system, that is, in the observation system E, the object has moving in one direction, but for the observation system B the object has moving in the opposite direction. At the same time, taking into account significance μ0=1/c, other differences are absent. In other words, we get completely independent opposite surveillance systems without communication with each other, that is, these are systems closed into themselves. If we make the transition to the general observation system with the introduction of a new variable (this approach is often used in quantum mechanics) μ0=1/(cuп), then the last equation of magnetic induction in (39) corresponds to the correct dimension, but the first equation of electric induction in (39) has not the correct dimension. For the first two equations in (39), taking into account the dimension of the "correct" record, it is necessary to have the form:
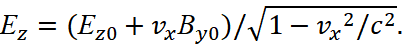(40)
This is exactly what Feynman did by analogy with the transformations of length and time according to the Lorentz formulas:
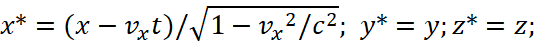
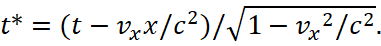(41)
That is, he made an adjustment to the result due to the fact that he took the magnitude c = 1, and then arbitrarily introduced an asymmetry to the magnitude in c2, as opposed to the resulting formulas (39). In fact, Feynman, on the basis of the first two equations in (39) and equations in (40), presented a new law of coupling of electromagnetic components not through Maxwell's equations, but through space-time curvature by Lorentz’s transformations by analogy with length and time. In other words, he introduced duality and ambiguity.
In this case, the electromagnetic components E and B simply cannot has propagation at the speed of light and have wave properties, since the equations for (39) and (40) coincide one into one with the equations for length and time according to the Lorentz transformations (41). The difference concerns only the fact that we observe the magnitudes E and B in result of their interaction in environment according to the laws of physics, but in our observation system the parameters of length and time although have a connection in SRT, but we do not observe a projection along time in environment inside of three-dimensional system. Considered the paradoxes given above, one could refuse duality in favor of Maxwell's equations, but the fact is that such transformations have some confirmation in the Lorentz force. Indeed, if we proceed from the initial absence of an electric field in the form of Еу0 and Еz0, then when multiplying both parts of equation (40) by the charge q, we have a representation of the classical Lorentz force:
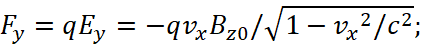
(42)
In other words, the derived formulas can be used, but only without taking into account the interaction of opposites, similar to how Newton's third law is used. At the same time, the significances of the electric field strength and magnetic induction belong to different systems of coordinates. Accordingly, for magnetic components we have:
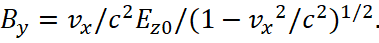(43)
However, the question follows: "How to exclude the initial magnitudes of Ey0, Ez0 and By0, Bz0 if they are included in the components taking into account the Lorentz’s transformations?" It is clear that if we exclude Еу0, Еz0 from (39), then we will not take into account the transformations by (43), and if we set the excluding of Ву0, Вz0, then we can forget about the Lorentz’s force. At the same time, formulas (42) and (43) contradict even the form of the classical Maxwell equations and have a "degenerate form". We show this on the basis of the transition to wave equations. Let's write the first equation in (42) without taking into account the charge of particle in the form of increments:
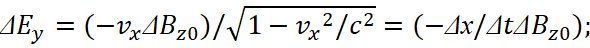
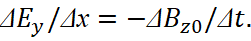(44)
Here, we have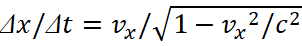 
. We replace increments of magnitudes through differentials:
(45)
In other words, instead of the equation of subordination of electromagnetic components to the Maxwell equation, we get the continuity equation. At the same time, we have a new law of transformation of electromagnetic components into each other, in addition to even the classical Maxwell equations with presence of ambiguity. Let us apply a similar approach with the same reasoning to the magnetic component from equation (43):
(46)
Here, too, the Maxwell equation is being substituted through the continuity equation. Next, we differentiate the equation in the system (45) along x, and the equation (46) along t. What is the difference here from the derivation of the equation of a planar electromagnetic wave? In effect that the left and right sides of equations (45) and (46) will coincide up to a multiplier c2 if Ey=Ey0 and Bz=Bz0. If we assume this, we get the equation of a planar electromagnetic wave:
(47)
If we proceed from the system of equations (39, 40), such equality Еу=Еу0, and Bz=Bz0 is possible only if the members with the velocity of motion are zero. In other words, we have a paradox in which the obtained equations (39, 40) contradict the possibility of forming even a flat electromagnetic wave due to inequalities Еу≠Еу0 and Bz≠Bz0. Hence, the belonging of components in formulas (39, 40) to electromagnetic components is already initially excluded. Thus, we see that due to the components of length and time, which obey the Lorentz’s transformations, we can influence the electromagnetic components, but the form of the equations obtained in (39, 40), as already noted above, does not correspond even to the classical Maxwell equations. This means the ambiguity of the laws of physics, and it cannot be, since this implies a violation of the law of conservation of quantity and, thereby, the existence of any laws other than miracles is generally denied.
However, physicists ignored the paradoxes and decided to describe the change of the electric field by Lorentz’s transformations based on the equations obtained by Feynman (39, 40), but with the involvement of the CGS calculus system, which express Maxwell's equations in the form [10]:
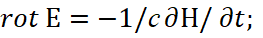
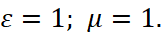(48)
If we take into account that H=cE, then we have two contradictory equations:
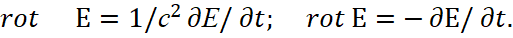(49)
In other words, the paradox of the CGS system is the fact that this measurement system does not take into account the constants of electric and magnetic permeability, even for vacuum. Hence, E and B do not differ from each other, except by changing the direction of movement, and this was expressed in the form of equations [11]:
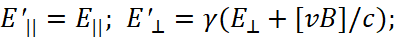
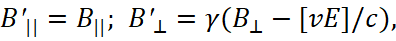(50)
ere the symbols || and ⊥ denote, respectively, the longitudinal and transverse components of the vectors,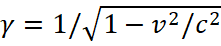 
. In this case, we obtain the Coulomb and Lorentz force relationship when multiplying the electric field strength by the charge q in the form:
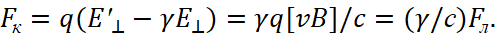(51)
In this case, the Coulomb’s force and Lorentz’s force have a relativistic addition. Actually, this form corresponds to the first equation in (18) in the form ΔЕy=ΔEt/(1-vпр2/с2)1/2 at taking into account the difference in the speed of light, but this does not take into account the interaction between opposites. A similar view also without the coefficient associated with the speed of light, which can be attributed to the CGS system, instead of the SI system, we will get below. It is clear that the difference between our approach and the approaches of physicists in electrodynamics is due to the fact that in our theory the velocity according to SRT reflects the velocity in contrast system, because in our observation system the field strengths have a rate of change equal to the speed of light.
In reality, physicists in electrodynamics replaced the intensity of electromagnetic fields through magnitudes of length and time, and therefore were able to use the magnitude of velocity in our system of observation. Practically, they recognized that space and time in one opposite looks like electromagnetic components in another opposite, that is, they have already done this before us. In other words, physicists came to the results obtained by us, but by the method of fitting to the result. The inverse transformations are obviously obtained by replacing v→-v. At the same time, if there is only a magnetic field B' in a moving system of observation Σ', then in a motionless system Σ, according to (50), a transverse electric field will appear E=-[vB]/c. Similarly, if there is only an electric field E' in the system Σ', then a transverse magnetic field В=-[vЕ]/c will appear in the system Σ. Next, we consider the problem about finding an electromagnetic field created by an elementary charge of particle q (in our case it is q=± 1 in accordance with Dirac theory), and this particle has moving with a constant velocity v. In the own system of coordinates Σ' of charged particle, there is only an electric field with intensity:
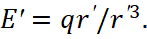(52)
Further, applying the inverse conversion formulas to (50) and the writing their in compact form, we have:
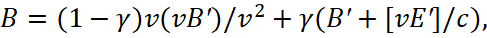(53)
We will find that in a motionless system Σ:
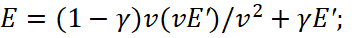
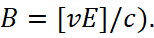(54)
Substituting here the magnitude from (52), and considering that according to the Lorentz’s transformations we have representation:
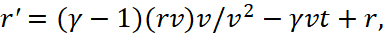(55)
We find after simple transformations:
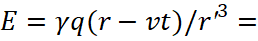
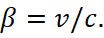(56)
Accordingly, for x=0, y=0, z=1 and t=0 we have:
E=q/1-(v/c)2.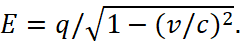
(57)
The formula (57) coincides with the formulas (17), if you change the designation E to τ, and q to τ0. Hence, it is concluded that the compression of electric lines of force occurs in the cross section due to the member 1/[(1-(v/c)2)]1/2.
However, the coincidence of the laws of physics means that we are not dealing with opposite objects, due to the fact that the difference can be identified only by the ambiguity of the laws for objects. But, this, with such approach in classical electrodynamics, is not being observed. Indeed, a mathematical substitution of variables under the same physical law cannot be considered a varying of real physical properties, and then E and q are τ and τ0. The difference between E and H from τ and l due to fact that the electromagnetic components have transformations with the speed of light in accordance with Einstein's SRT, but for τ and l in this case we have either infinitesimal magnitudes or infinitely large ones due to the transformation in the form of a member [(1-(v/c)2)]1/2, which contradicts the presence of such constants of the universe as Planck's constant and the speed of light. In addition, here we immediately see a paradox in the variant of classical electrodynamics due to the identical representation in (50) for electric and magnetic components, in which we have E=-[vB]/c and B=[vE]/c. From here, after substitution, it turns out:
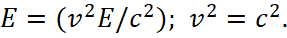(58)
In other words, only one option is possible here, when v=c. The form of the formula (58) fully corresponds to the form of the formula (31). Accordingly, if we present an electric field in (54), we also get a paradox in the form:
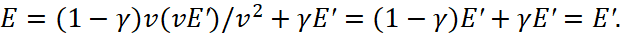(59)
Next, we take into account that equation (54) by virtue of relativity by Einstein's SRT is also transformed to the form:
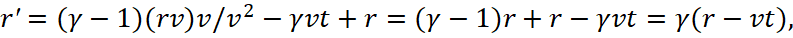(60)
In other words, the equations (59) and (60) are not related in any way, as there is no law of transformation of one significance into the other significance. This means that the electric field is completely independent of the Lorentz’s transformations.
Hence, the variant presented in classical electrodynamics means an adjustment to the result and this is due to the fact that the obtained independence of the electric field and length is associated with the absence of a projection along time for the electrical component.
It is clear that the conclusion of magnetism as a relativistic effect in electrodynamics is also paradoxical [8], by analogy with the formula (42), that is, the relativity of magnetic and electric fields is considered, and again the electromagnetic components are represented as space and time according to Einstein's SRT, that is, the movement of electromagnetic components at the speed of light is excluded. In order to solve the paradoxes, Feynman considered mobile and motionless systems (fig. 5).
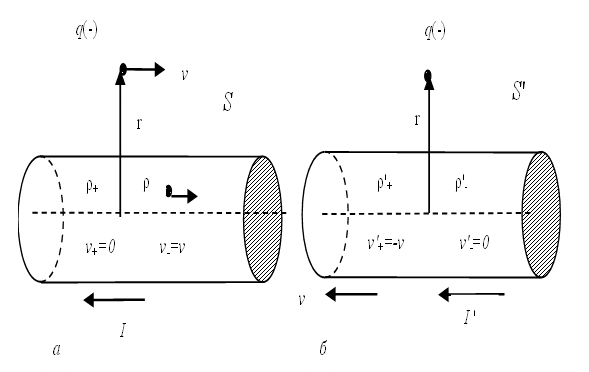
Fig. 5. The interaction of a wire with a current and a particle with a charge q, considered in two coordinate systems: a) the wire is motionless in the S system; b) the charged particle is motionless in the S' system
We consider that the negative charged particle q(-) has motion in parallel for the wire through which the current flows I (fig. 5, a), which corresponds to the observation system S. In this case, the Lorentz’s force is directed towards the wire, and this force, taking into account the magnetic field at a distance r from the axis of the wire, is defined as:
(61)
At the same time, Feynman believes that the conductor is electrically neutral, since the density of fixed charged particles ρ+ in the S system should be equal to the density of charged particles ρ- with the opposite sign, that is, we take an uncharged wire, and in this case there is no electric field outside the wire.
Actually, this statement regarding an external charged particle in motion is being refuted, since magnetic forces are replaced by electric forces in the future, taking into account the fact that the density of charged particles in the wire (but not the charge itself) is subject to changes in accordance with Einstein's SRT. In this case, the electric field of a negative charged particles q moving at a speed v0 relative to the wire in the system S in accordance with SRT should have a higher intensity relative to motionless positive charged particles (fig. 4), similar to how it is seen from the electric field strength for a charged particle in motion [12], and it leads to increased interaction with attraction in accordance with the formula:
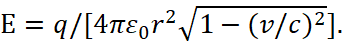(62)
In other words, the subordination of the electric field to the space-time curvature is considered. This means that the compression of electric forces is observed both in the system S and in the system S', the difference is only in the change of the direction of movement of the charged particle. Note that the magnetic force also does not change its magnitude relative to the system of positive and negative charged particles, because in both cases, both in the system S and in the system S', there is movement. But let's look at the course of Feynman's reasoning, and in this cause he gets the connection of forces between positive and negative charged particles due to the motion. Accordingly, when we do switching to the current density, we have a representation of the Lorentz force in the form:
(63)
Here A is area of the cross-section of the wire. Next, we take a special case when v=v0, and the equation is rewritten to the following form:
(64)
In the S' system (fig. 5, b), a particle with a charge q is motionless and the wire has motion to the left with a velocity v relatively of particle. Positive charged particles moving together with the wire will create some magnetic field B' near the particle, but the particle is now "at rest", so the magnetic force does not act on this particle.
If there is some kind of force (here the laws of physics on interaction should not depend on the observation system, otherwise the events of the phenomena occurring in different observation systems would differ, and this would mean that you can get away from the event by changing the observation system), then this should consider due to the electric field. But this can be done only if the wire turns out to be charged, that is, it should turn out so that the neutral wire with a current appears charged if this wire is set in motion. To get such a result, Feynman attracted STR of Einstein. Moreover, he believed that the so-called electric charge q does not depend on the speed of movement (otherwise it would mean that the sum of positive and negative charges is not equal to each other due to movement), but the density of the charged particles is being changed with the movement of the wire depending on the change in its length according to the formula:
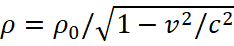(65)
Accordingly, at moving, the length of the conductor has the change (decreases):
(66)
Equation (65) is derived from the condition that the charge in any coordinate system is conserved in terms of quantity in accordance with what is observed:
(67)
The density of the motionless positive charges in the system S is equal to ρ+. However, in the S' system, where the wire has the motion at a speed of v, the density of positive charges becomes equal:
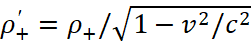(68)
Negative charges in the system S' are motionless, so their charge density is equal to the density of motionless charges ρ0=ρ-'=ρ-, and in the system S at their velocity v we get:
(69)
Here, the density of the negative charge began to play the role of length according to the formula (66) and in fact this means that in a motionless system, the charge density in the cross-section is less than we have in condition of the moving. Further, the resulting charge density ρ' is determined by the formula:
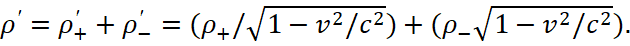(70)
In fact, if in the significance ρ+' we mean the length according to the first formula (17) ρ+'=l in the S' system, but in the significance ρ-' we mean the time according to the second formula (17) with recalculation onto the length ρ-'=сτ in the S' system, then we have an analogous result. And this suggests idea that opposite charges display equivalents of length and time in relation to each other, which means their invariant exchange in accordance with Einstein's SRT.
In other words, physicists have already characterized opposite charges without us, as the interaction of opposites connected through the speed of light through exchange in the form of equivalents of length and time. Actually, such a conclusion is inevitable, because only in this case there is a reason for the formation in space and time of sources for the synthesis of secondary waves, taking into account absorption and radiation. This actually refutes the presence of a charge as something contained in space and time. Since the motionless wire is neutral, that is, it is observed -ρ+=ρ- from hence we get:
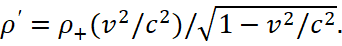(71)
Thus, it turns out that the charge density (or electric field strength), depending on the velocity, if we consider the system of the sum of positive and negative charges, taking into account their interaction, is determined not by formulas (65) and (62), in accordance with SRT, but by formula (71). On the base of formula (71), the electric field at a distance r from the axis of the cylinder is calculated:
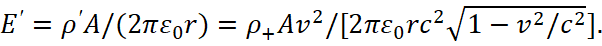(72)
Then the force in the system S' has magnitude:
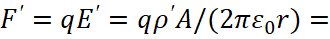
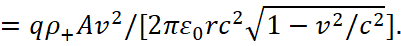(73)
As a result, we have a connection:
.
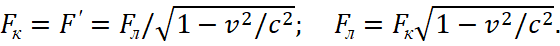(74)
Here we have a difference between electric and magnetic forces by a magnitude 
similar to (42), but this is true only if opposite charges act in relation to each other as interacting opposites, that is, objects expressing the equivalents of length and time.
Accordingly, the Coulomb's force and Lorentz’s force, in this case of the interaction of charges, act as forces that ensure the invariance of their interaction in any system of observation. In practice, the subordination of the Coulomb's force and Lorentz’s force to SRT transformations means a closed transformation of the Coulomb’s force into the Lorentz’s force, and vice versa, similar to the transformation of length and time. Hence, the magnetic and electric components define opposites connected through the speed of light, which belong to different systems of observation, as in (42). This effect is completely determined by the fact that there is a relationship associated with the transformation of electromagnetic components into lengths of coordinates and into magnitude of time, and vice versa, otherwise it would be impossible to subordinate electromagnetic components to Lorentz-Minkowski transformations. However, we see that according to (74) there is no closure, as there is a transformation from velocity in only one direction (for example, from the Lorentz’s force to the Coulomb’s force), and this problem was solved by the inverse transformation, and hence physics attributed the connection of forces on the base of changing along magnitude of time. That is, the difference between the Coulomb's force and Lorentz’s force disappears if we take into account the relativistic effect associated with the time change in the S and S' systems. Its essence is that the transverse momentum of the charged particle q in the direction of the conductor should be the same, both in system S and in system S'. We denote the transverse coordinate y and will compare magnitudes Δpy and Δpy', using the relativistic correct equation of motion:
F=dp/dt (75)
During the time Δt, the particle will acquire a transverse momentum Δpy in the system S, in accordance with the expression:
Δpy=FΔt. (76)
At the same time, in the S' system, the transverse momentum is equal to:
(77)
Since the particle we are considering was initially at rest in the S' system, then for small Δt:
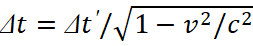(78)
Then, after substituting the significances from (76) and (77), we have:
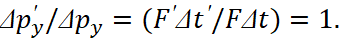(79)
We see that two opposites (two observation systems) have actually been introduced without us, where, for example, the connection of the Coulomb's force and Lorentz’s force is considered in the observation system from the opposite related to length, and the inverse transformation is determined by the observation system related to time.
Thus, the invariance (closed transformation) between the Coulomb's force and Lorentz’s force is achieved on the basis of the interaction of two global opposites, taking into account the common space-time continuum and electromagnetic continuum. And since the system of the universe is a closed system and length and time in the global systems of opposites have the changing by places with the change of kinetic energy to potential energy, and vice versa, the Coulomb’s force in one opposite will look like the Lorentz’s force in the other opposite, and vice versa. In other words, despite the adjustment to the result due to the fact that initially the consideration of processes took place only taking into account one opposite, physicists received particular solutions that coincide with practice in one global opposite. And this did not give a complete picture of the interaction, which actually led to the fact that the Bohr could not solve the problem of replenishing energy for an electron at moving along orbit.
In other words, our solution for the coupling of electromagnetic forces according to the formula (22), taking into account Einstein's SRT, differs from the solution (74) as we takes into account the presence of changes (movements) not in one opposite (observation system), but in two global opposites. In our case, it is impossible to get the falling of an electron on a proton, since the additional mass of the proton is associated precisely with the kinetic motion of the positron around the antiproton in contrast system.
This is exactly what the Bohr did not take into account when considering the problem of the rotation of electron around a proton and he came to the conclusion that an electron falls on the nucleus due to radiation during accelerated motion. The fall does not occur because the radiation in one opposite is compensated by the radiation in the other opposite due to symmetry, which is associated with the law of conservation of quantity. In this case, the forces of attraction and repulsion in one opposite are associated with motion (kinetic energy) in the other opposite, and they form each other.
An important conclusion of our analysis of the Coulomb’s force and the Lorentz’s force, based on the well-known equations, is that both the Coulomb’s force and the Lorentz’s force are associated with changes (and this is expressed through movement in space and time) in opposites. At the same time, the Coulomb's force (in the form of electric field strength) begins on a positive charged particle, which can be interpreted as the system of one opposite through reflecting of length, and this force of has end on a negative charged particle, which can be interpreted as other system of opposite through reflecting of time. Thus in fact in our observation system we see through this force a reflection of the processes of change (movement) with the subordination of SRT in the system of opposite. The Lorentz’s force reflects these changes already in our observation system. It is clear that the Coulomb’s force and the Lorentz’s force in the opposite observation system are replaced by each other.
Actually, such a result followed from the calculations made by physicists, but it was template based on the representation of the world from one observation system and it excluded correct conclusion.
Let's imagine the formula (72) based on the relationship of velocities in two opposites. Then we must take into account that we have 
, from here we get:
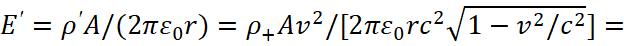
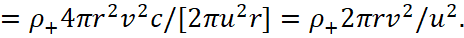(80)
Next, we take into account that the minimum radius for a particle is determined by the Planck constant h/(2π) and at the same time hc = 1, as a result we have
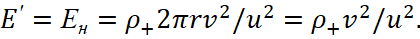(81)
In result, we imagine the presence of a charge density as the equivalent of the electric field, since the charge density is determined by the divergence from the electric field. Accordingly, we get:
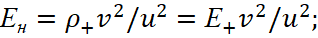
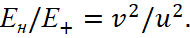(82)
In other words, the strengths of magnetic and electric fields are directly related to the magnitudes of velocities in two opposites. And this means that the Coulomb's force in one opposite reflects the Lorentz's force in the other opposite, and vice versa.
Absent of understanding of the Lorentz's force and Coulomb's force as the forces arising from the existence of the simplest objects of the form of electronic and muonic neutrinos (antineutrinos) led to the fact that the force of pressure of light in the well-known experiment of P.N.Lebedev began to be considered as a repulsive force based on the Coulomb's force and Lorentz's force.
However, we note that we have shown, in section 2, how from the improved Maxwell equation reflecting an electronic or muonic neutrino (antineutrino), the total interaction force is obtained from the Coulomb and Lorentz forces based on the intensity of electromagnetic fields. The force giving pressure of light is determined by the interaction of two simplest objects based on an electronic and muonic neutrino (antineutrino), that is, it is a more complex interaction involving three objects, one of which is a charged particle, and the other is a photon consisting of an electronic and muonic neutrino (antineutrino). Actually, how a corpuscular particle gets the velocity magnitude of the corresponding kinetic energy of an electromagnetic wave, we have shown in [1].
In addition, with the usual Maxwell equations and at motion at the speed of light, an electromagnetic wave of the form (47) cannot have electromagnetic components along the direction of propagation, and it means here we have nothing to exert pressure on the object. And the point here is that in equation (47) there is no member forming the interaction with the propagation medium, which, by the way, excludes the propagation of the wave around the obstacle. Therefore, in order to influence the propagation medium, and it is also any corpuscular object, it is necessary to consider an electromagnetic wave with radiation and absorption sources taking into account formula [13]:
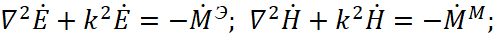
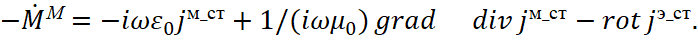(83)
According to our theory, based on the improved Maxwell equations, we have the form [4]:
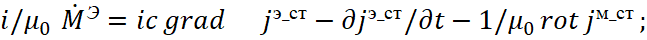
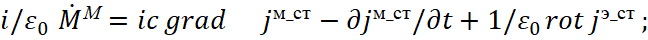
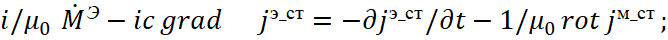(84)
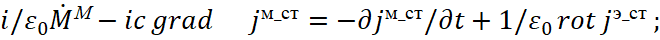
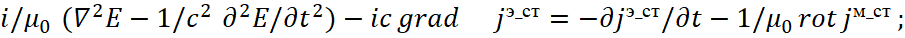
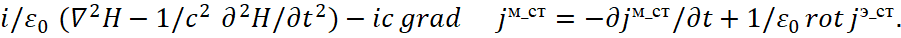
The formulas (83) and (84) gives exchange and interaction. And such formation of an electromagnetic wave implies a combination of the formation of wave components of the electric and magnetic field intensity through the interaction of electronic and muonic neutrinos (antineutrinos). However, in electrodynamics, the force of pressure of light was taken on the basis [14]:
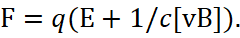(85)
At the same time, it was proposed to use the Lorentz’s force density in the form:
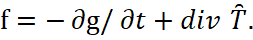(86)
or in components
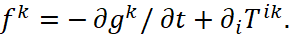(87)
where
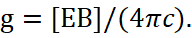(88)
Here T is the Maxwell's stress tensor having components
(89)
Next, physicists are inviting to understand the physical meaning of g and Tik. With this purpose the law of conservation of momentum is used to show that a mechanical impulse must be attributed to the electromagnetic field. Then, the sources of the electromagnetic field and it are the free charged particles and currents, are concentrating in a certain volume V with surrounding by a fixed surface S, and have a mechanical impulse P. At the same time, it is assumed that there is a mechanical pulse of the electromagnetic field in the same volume, which is indicated by the symbol G. In other words, a mechanical impulse was also attributed to the electromagnetic field; otherwise there would be no connection in one equation. However, how this mechanical electromagnetic pulse should be formed in the direction of motion at the speed of light, if the components of the electromagnetic field are perpendicular to the direction of motion, remains a mystery. As a result, the total pulse of the "field + sources" of system can change only as a result of the flow of the impulse of the electromagnetic field through the surface S. Therefore, we can write:
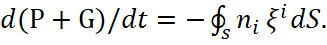(90)
Here ξi is the density of the impulse flux of the electromagnetic field in the i-th direction. At the same time, according to the second law of dynamics, the force acting on sources from the electromagnetic field is equal to:
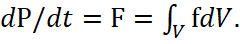(91)
Or if we take into account the formula (86):
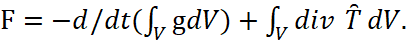(92)
Further, converting the last integral to the surface using the Gauss-Ostrogradsky theorem, we find:
(93)
Here: g is the pulse density of the electromagnetic field, and Tik is the flux density of the k-th component of the impulse of the electromagnetic field in the i-th direction. A comparison of this formula with formula (90) shows that:
G=VgdV=1/(4πc)V[EB]dV.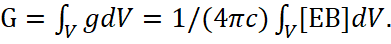
(94)
The latter formula actually means that the mechanical impulse in the direction of motion gives a vector multiplication of the electric field strength and magnetic induction, and this magnitude determines the energy of the electromagnetic field in the direction of motion. It is clear that when the photon energy is transferred to a particle, the energy of the electromagnetic field is absorbed by the particle, and there are no violations in the transfer of the amount of energy here. However, this does not solve the problem in any cause, according to which it was necessary to show how, due to the forces of electromagnetic field strengths according to Coulomb's law and Lorentz law, the particle receives kinetic energy in the direction of photon motion.
Hence the question: "How should a force be formed in the direction of motion, if the speed of movement of electromagnetic components is the speed of light, and the presence of such a force in the direction of motion would mean that a speed higher than the speed of light is possible?" The only option is that the electromagnetic components must interact with the surrounding space-time curvature, and the interaction is associated with exchange and mutual transition (transformation). This is where the type of electromagnetic wave with the presence of radiation and absorption sources is required. It should be understood that physicists themselves have seen the errors of this approach, so they justified such an interpretation of g and Tik on the grounds of simplicity, since representations (88) and (89) are not the only ones. It is not difficult to see, that there are countless combinations of fields and their derivatives that turn the right part (86) to zero, that is, to identical zero by virtue of associative summation. In addition, obtaining the pressure force of light in the form of (86) already has an initial paradox, since the pressure of light must be exerted in the direction of the electromagnetic wave, and the divergence corresponds to the direction of the force in all directions and this means the presence of charges, but not of electromagnetic fields which have the motion at the speed of light. Hence, it would be more correct to write equation (86) in the form:
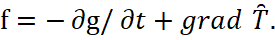(95)
And this resulting form of the equation is very similar to a variant of the conditions for the auxiliary function, which is a vector potential, in the form:
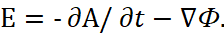(96)
At the same time, in article [4], we showed how the improved Maxwell equations with projections of electromagnetic components along magnitude of time are obtained on the basis of vector potentials, and accordingly we showed the production of electromagnetic waves with sources of radiation and absorption, and it is required for the interaction of electro-magnetic components with space-time curvature! Thus, we come to the conclusion that although physicists tried to represent the pressure of light through the Lorentz’s force and Coulomb’s force on the basis of electromagnetic components, they did not take into account the connection of electromagnetic components according to projections, taking into account the direction of electromagnetic forces in cross-section to the direction of wave motion. Hence, the physics of the interaction of the process was presented through the final stage - the transmission of energy on the base of impulses. At the same time, it turned out that in order to describe the process of transfer of energy itself, it is necessary to represent the pressure force of light in the form of (95), since otherwise the interaction of electromagnetic components with space-time curvature cannot be obtained.
The very essence of pressure of light cannot be described on the basis of Coulomb’s force and Lorentz’s force, and it has a more complex character. According to our theory, the essence of the effect is based on the fact that in order to transfer electromagnetic energy to an electron in the direction of motion, it is necessary to have a system of closed solutions in the form of Dirac equations, which we showed in article [1] and private electronic and muonic neutrinos (antineutrinos) do not have closed solutions, in the sense that they have a difference onto the coefficient associated with motion in the systems of opposites. In this case, the interaction of an electronic and muonic neutrino (antineutrino) is necessary, and it gives closure based on the fact that the coefficient associated with the motion in the system of opposites for these elementary objects has an inversely proportional relationship. Thus, we have obtained, that any force action on an object occurs due to the absorption or radiation of the simplest objects of the universe - of electronic and muonic neutrinos (antineutrinos), and the Coulomb’s force and Lorentz’s force, like all other forces, are followed from the equations of these simplest objects and their interactions, that is, from system of equations on the base of the Dirac system of equations. In this article, we have found out what the errors and paradoxes were in establishing the electromagnetic continuum separately from the space-time continuum.
Conclusions:
- The absence of falling of an electron on the nucleus during rotation with radiation is due to the equality of the action force (Coulomb’s force) and the reaction force (Lorentz’s force).
- The Lorentz’s force and Coulomb’s force are the result of interaction based on electronic and muonic neutrinos and antineutrinos.
- Feynman's attempt to describe the subordination of electromagnetic components to Lorentz’s transformations through vector potentials gave an erroneous result, in which we have symmetry in the transformation of electric and magnetic components according to formulas (39). However, this would mean that there is no difference between the electrical and magnetic components and then they are not opposites. And this means the paradox of uniformity. In this case, we should have observed the Lorentz’s force depending on the velocity and the electrical component, but there is no such force.
- The use of the CGS system according to formulas (48) on the base of transformations according to formulas (39) is also not correct due to the fact that in addition to the erroneous approach according to formulas (39), errors are added due to the lack of consideration of parameters of environment according to (48).
- When describing the general electromagnetic continuum according to Fig.5, Feynman actually equated the presence of negative and positive charges to the equivalents of length and time, and thereby excluded the presence of charges separately from space and time else early before us.
- Considering that the charged particles are expressed through space-time curvature, and at the same time, the Coulomb's force and Lorentz's force are also related as length and time through Einstein's SRT, then considering length and time as global opposites closed to each other with mutual transformation and influence, then the Coulomb's force and the Lorentz's force shall act as the opposing forces to each other. In this case, the Coulomb force in one observation system acts as the Lorentz force in the opposite observation system associated with the first through the speed of light.
- The approach in classical electrodynamics with the derivation of pressure force of the light on the base of the total Lorentz's force is also incorrect, since the transmission of momentum occurs due to the interaction of an electromagnetic wave with a particle, and not on the base of the Coulomb's force and Lorentz's force, which are derived from one improved Maxwell equation. Another words we have interaction of some elementary objects.
.png&w=640&q=75)
