Введение
Вот уже четвёртое столетие идёт со времени открытия закона всемирного тяготения, но вопрос о причинах гравитации до сих пор остаётся открытым. А без его решения невозможно определить границы применимости закона. Актуальность последнего усиливается тем обстоятельством, что коэффициент пропорциональности в формуле Ньютона для сил тяготения получен по результатам измерений лишь для очень малых масс, а применяется для описания взаимодействия тел любой массы вплоть до сверхмассивных космических тел.
Попыток найти модель тяготения, проясняющую её причины, предпринималось немало. Обстоятельный обзор и анализ таких работ выполнен И.И. Кагальниковой [1]. В конечном итоге все эти попытки оказались неудачными, т.к. исходили из допущений, не подкреплённых экспериментально, и выводы их нельзя было проверить опытным путём.
Особенно популярна в своё время была модель тяготения швейцарского физика Жоржа Луи Лесажа, предложенная в 1784 году. Суть модели в том, что мировое пространство заполнено мельчайшими твёрдыми частицами, движущимися с огромной скоростью во всевозможных направлениях. Отдельное тело, подвергаясь со всех сторон бомбардировке частицами, должно оставаться в равновесии. Но если по соседству с ним находится другое тело, то оно экранирует часть потока частиц, движущихся в сторону первого тела, и в результате возникает сила, толкающая первое тело ко второму. Таким же образом экранирующее действие первого тела заставляет двигаться к нему второе тело. Несколькими годами ранее подобные взгляды высказывал М.В. Ломоносов, поэтому такой подход к проблеме гравитации называют ещё гипотезой Ломоносова – Лесажа. Эта гипотеза «благодаря своей исключительной простоте и физической наглядности быстро привлекла к себе всеобщее внимание естествоиспытателей и на протяжении последующих полутора столетий послужила темой страстной полемики. Она вызвала огромное число публикаций…, многочисленными авторами предлагались различные модификации гипотезы Ломоносова – Лесажа. Однако более тщательное рассмотрение каждой из них неизменно приводило к выводам, несовместимым с теми или иными представлениями классической физики. По этой причине, а также в связи с успешной разработкой общей теории относительности, интерес к гипотезе Ломоносова – Лесажа в начале 20 века резко снизился и, по-видимому, она была бы предана полному забвению, если бы в 1919-1922 гг. итальянский учёный Мажорана не опубликовал результаты своих в высшей степени интересных опытов. В серии весьма тщательно поставленных экспериментов Мажорана обнаружил явление поглощения гравитации массивным экраном, расположенным между взаимодействующими телами, - феномен, легко интерпретируемый в рамках классических представлений о механизме тяготения, но не имеющий до сих пор объяснения с позиции общей теории относительности.» [2, с. 3].
Впрочем, сама общая теория относительности Эйнштейна была принята далеко не всеми физиками. Так, крупный французский учёный Леон Бриллюэн охарактеризовал её как «блестящий пример великолепной математической теории, построенной на песке и ведущей ко всё большему нагромождению математики в космологии (типичный пример научной фантастики)» [7, c. 28]. Столь нелестная оценка теории оказалась возможной вследствие её слишком скудного экспериментального подтверждения. Завершив её создание, «Эйнштейн предсказал ряд эффектов, которые можно было надеяться проверить на опыте. С тех пор было затрачено много труда и получено очень мало практических результатов. Прежде всего следует указать со всей ясностью на то, что такого рода эффекты не являются специфическими только для теории Эйнштейна; используя соотношение между массой и энергией, можно получить аналогичные результаты приблизительно того же порядка величины.» [7, с. 130]. Более того, далее (на следующей странице) Бриллюэн, ссылаясь на Шази, который занимался вычислениями смещения перигелия четырёх планет и нескольких спутников планет, отмечает, что один из предсказанных Эйнштейном эффектов (смещение перигелия Меркурия), хорошо подтвердившийся в опыте, что называли блестящим подтверждением предсказания теории, не нашёл подтверждения в ряде других примеров в солнечной системе – теория приводила к ошибочному или даже имеющему противоположный знак результату.
Движущим мотивом для Эйнштейна при создании общей теории относительности было обобщение результатов специальной теории относительности, рассматривавшей инерциальные системы отсчёта, двигающиеся относительно друг друга прямолинейно с постоянными скоростями, на системы, движущиеся с ускорением. Фактически это вылилось в создание нового варианта теории тяготения, являющегося по мнению автора этих строк геометрической интерпретацией теории Ньютона. Приведенные выше фрагменты критики общей теории относительности показывают, что она ничего не дала для практических потребностей физики. Но как попытка установить связь между материей, пространством и временем, она представляет интерес в мировоззренческом плане.
Представленная в данной работе модель гравитации также является модификацией модели Лесажа. И полученные уже с её помощью результаты вселяют уверенность, что данная модификация может быть основой для теории тяготения более общей, чем теория Ньютона, и включающей её как частный случай.
Вывод основных соотношений
Перейдём к существу модели. Заменим в модели Лесажа мельчайшие твёрдые частицы частицами, не имеющими массы покоя, движущимися со скоростью света (c) и электрически нейтральными, а потому обладающими громадной проникающей способностью. Из известных сейчас элементарных частиц подобными свойствами обладают нейтрино, которые крайне слабо взаимодействуют с веществом и свободно пронизывают такие космические объекты, как Солнце, а тем более Земля. Но отождествлять нейтрино с нашими гипотетическими частицами, наверное, нельзя или преждевременно, поскольку считается, что нейтрино имеют массу покоя, хотя и крайне малую [6, с. 348]. И в то же время близость свойств нейтрино к свойствам наших гипотетических частиц создаёт уверенность, что частицы с подходящими свойствами должны быть. Учитывая, что уже существует традиция называть частицы гравитационного поля гравитонами, будем их здесь называть так же.
Пусть в каждый момент времени в единичном объёме свободного пространства находится n0 гравитонов, массу (движения, массы покоя, как отмечалось выше, у гравитона нет; далее это не будем оговаривать) каждого гравитона обозначим через µ и соответственно его импульс будет равен p = µc. Выделим в пространстве произвольно плоскую площадку dS и определим поток импульса гравитонов через неё. С этой целью будем использовать методы, применяемые в молекулярной физике при выводе формулы для давления газа на стенку сосуда [4, с. 47-56]. Ход вывода искомой формулы поясняется схематическим рисунком (рис.1).
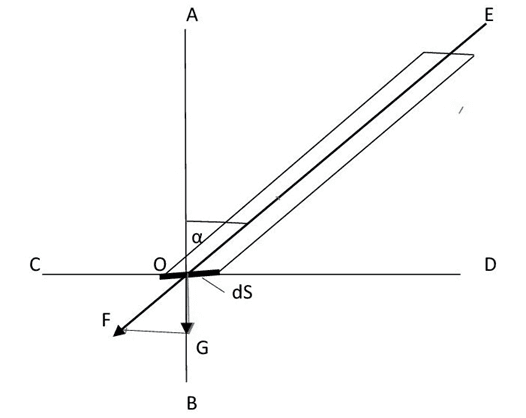
Рис. 1
Для простоты рисунок дан в плоском виде – вследствие симметрии относительно оси АB, нормальной к dS, картина в любом сечении по этой оси будет такой же (подразумевается, что площадка dS – это круг). Рассмотрим движение гравитонов вдоль какого-то направления EF, проходящего через центр выделенной площадки dS и составляющего с осью АB угол α. Построим наклонный цилиндр, считая dS его основанием, так чтобы его образующие были параллельны направлению EF. Длина образующих цилиндра равна модулю скорости c, а его объём равен dV = dS c cosα. При этом количество гравитонов в этом цилиндре в каждый момент времени будет равно dn = n0 dS c cosα. Из них сквозь площадку dS пролетят за единицу времени гравитоны, направление движения которых лежит в пределах телесного угла dω = sinα dα dφ, где φ – угол поворота вокруг оси AB. Полный телесный угол, соответствующий всем направлениям движения, равен 4π. Отсюда количество гравитонов, пролетевших через dS, равно d2ns = dn dω/(4 π). Подставляя выражения для dn и dω, получаем:
d2ns =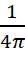 
n0 dS c cosα sinα dα dφ.
Разделив это на dS и умножив на cosα (проектирование на направление нормали к dS), получаем дифференциальное уравнение для плотности потока гравитонов в свободном пространстве:
d2qg =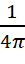 
n0 c cos2α sinα dα dφ.
Умножив полученное выражение на µc, получаем дифференциальное уравнение для плотности потока импульса гравитонов:
d2q =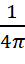 
n0 µ c2 cos2α sinα dα dφ. (1)
Интегрируя его по dφ от 0 до 2π, а затем по dα от 0 до π/2, получаем формулу для плотности потока импульса гравитонов в свободном пространстве:
q0 =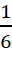 
n0 µ c2. (2)
Для оценки величины доли потока элементарных частиц, поглощаемых при прохождении через вещество, принимается за основу применяющийся в оптике экспоненциальный закон Бугера [5, с. 227]. Но при этом учитывается известный экспериментальный факт, что потоки разных элементарных частиц сильнее поглощаются материалами, имеющими большую плотность, для чего в показатель степени вводится дополнительный параметр ρ – плотность поглощающего вещества (предполагается, что поглощающее тело однородно). И закон поглощения частиц (здесь – гравитонов) получает следующий вид:
q2 = q1 exp (- ɛ ρ l), (3)
где q1 и q2 – плотность потока на входе в поглощающий слой и на выходе из него соответственно, ԑ – коэффициент поглощения, l – толщина слоя поглощающего вещества.
Поскольку проникающая способность гравитонов крайне велика, значение коэффициента поглощения будет очень малым. Поэтому для не слишком массивных тел показатель степени в (3) оказывается величиной, близкой к нулю, что позволяет использовать формулу приближённого вычисления:
exp (-x) ≈ 1-x. (4)
При этом выражение (3) становится линейным:
q2 = q1 (1- ɛ ρ l). (5)
Рассмотрим практически важный случай тел, имеющих форму шара. Пусть радиус рассматриваемого тела будет r. На входе в шар плотность потока импульса гравитонов равна q1= q₀ и определяется по (2). А на выходе из шара она уменьшается за счёт частичного поглощения гравитонов веществом шарового тела. Определим её величину. Поясняющий ход вывода необходимых зависимостей схематический рисунок рис.2 дан так же, как и рис.1, в плоском виде (разрез по большому кругу шара).
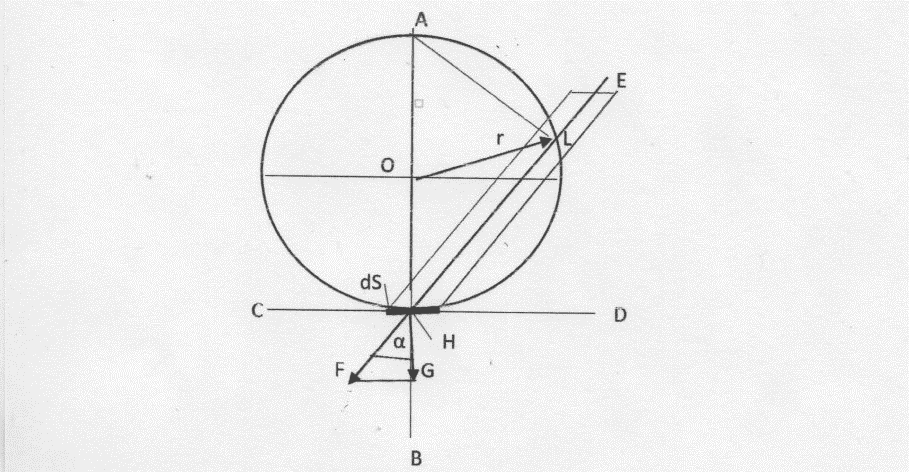
Рис. 2
Поместим элемент плоской поверхности dS так, чтобы он касался поверхности шара в точке H. Ввиду малости dS этот плоский элемент практически сольётся с поверхностью шара. Рассмотрим движение гравитонов вдоль какого-то направления, заданного хордой шара LH. Дальше действуем так же, как при выводе (2), отличие только в том, что здесь нужно учесть поглощение части гравитонов веществом шарового тела. Это можно сделать добавлением в дифференциальное уравнение (1) множителя exp (- ɛ ρ l) (или (1- ɛ ρ l) для не слишком массивных тел), где l – длина хорды шара на рассматриваемом направлении движения гравитонов. Кроме того, значение n0 выразим из (2) и в результате получаем:
d2 q = q₀ exp(-ɛρl) cos2α sinα dα dφ.
Как видно из Рис.2, l= 2 r cosα. Учтём это и проинтегрируем полученное уравнение по dφ от 0 до 2π и по dα от 0 до π/2. В результате получаем формулу для плотности потока импульса гравитонов на выходе из шарового тела:
qr = 3 q₀ ψ, (6)
где ψ =(2-e-a(a2+2a+2))/a3 и a=2 ɛ ρ r.
При отсутствии поглощения ɛ=0, а отсюда и a=0. При этом значение ψ получает неопределённость типа 0/0, раскрытие которой даёт ψ=1/3 и qr = q₀, что и должно быть в данном случае.
В случаях, когда можно использовать линеаризацию (5), получаем более простой результат:
qr ≈ q₀ (1-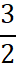 
ɛ ρ r) (7)
Умножая q₀ на площадь поверхности шара, получаем полный входящий в тело поток импульса гравитонов: Q1 = 4 π r2 q₀. Пройдя сквозь шар, поток импульса уменьшится за счёт частичного поглощения и на выходе будет равен, исходя из (6), Q2 = 12 π r2 q0 ψ. А при использовании линейной формулы (7): Q2 ≈ 4 π r2 q0 (1-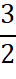 
ɛ ρ r).
Выходящий из шара поток по мере удаления от него остаётся постоянным, но плотность потока при этом уменьшается, т.к. поток распределяется на большую поверхность. Величина плотности потока на расстояниях от центра шара R ≥ r, равна qR = Q2 /4π R2. Отсюда:
qR = 3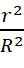 
q₀ ψ, (8)
А в случае не слишком массивных тел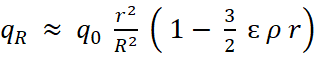 
или, учитывая, что масса шарового тела равна m = 
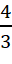ρ π r3:
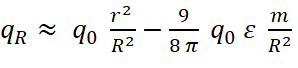. (9)
Посмотрим теперь, как будут взаимодействовать два шарообразных тела, плотность вещества которых ρ1 и ρ2, массы m1 и m2 и радиусы r1 и r2 соответственно. Расстояние между их центрами (O1O2) обозначим через R0. Для определённости будем считать, что r1 ≥ r2. Вначале рассмотрим более простой случай, когда оба тела не слишком массивны и поглощение гравитонов в них достаточно точно описывается линейной зависимостью (5). На рис.3 приведена схема, на основе которой выводятся необходимые зависимости.
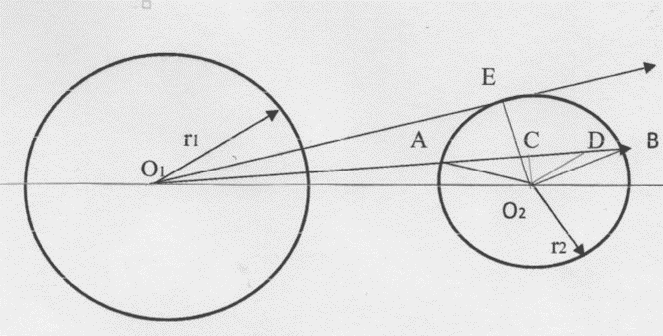
Рис. 3
Плотность потока импульса гравитонов после выхода из первого тела определяется по (9). Пусть во втором теле векторная линия потока импульса гравитонов со стороны первого тела проходит по какой-то хорде AB в направлении, составляющем угол α с осью O1O2, т.е. α=ےBO1O2. Максимальное значение α принимает, когда векторная линия лишь касается поверхности второго тела (в точке E), его величина при этом равна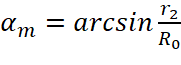 
. Возьмём на AB какую-то точку D, отстоящую от центра первого тела на величину O1D=R. На линию AB из O2 опустим перпендикуляр O2C, делящий треугольник ABO2 на два равных прямоугольных треугольника. Углом β между линиями O2C и O2D (β=ےCO2D) будем определять положение точки D на хорде AB. Максимальное значение этого угла равно βm = arccos (
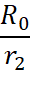sinα). Хорда AB равна 2R0 sinα tgβm, AD равно l = R0 sin α (tg βm + tg β), а дифференциал l равен dl=R0 sinα
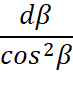. Отсюда плотность потока импульса гравитонов (q2) на длине dl изменится на величину dq2 = qR ɛ ρ2 dl. Учитывая (9), получаем:
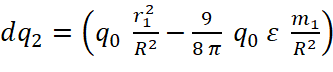ɛ ρ2 R0 sin α
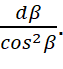(10)
Предположим, что первое тело абсолютно прозрачно для гравитонов (для него ɛ = 0, что равносильно отсутствию этого тела). В этом случае вместо (10) дифференциальное уравнение для плотности потока гравитонов во втором теле со стороны первого тела получит вид:
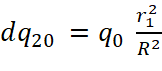ɛ ρ2 R0 sin α 
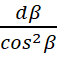. (11)
Тяготения в этом случае не возникает. Оно появляется из-за возникновения разности d(Δq2) = dq20 - dq2, которая, как следует из (10) и (11), равна:
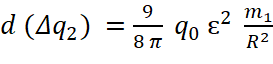ρ2 R0 sin α 
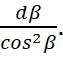(12)
Нас интересует в конечном итоге сила притяжения (F) всего второго тела к первому. Но сила F – это производная импульса по времени так же, как и поглощаемый в единицу времени поток импульса (ΔQ). Дифференциальное уравнение для ΔQ получаем умножением (12) на дифференциал площади по линии движения гравитонов, который равен dS = R2 sin α dα dφ (здесь φ – угол поворота вокруг оси O1 O2). Кроме того, поскольку тяготение вызывается только осевой составляющей сил, добавляем ещё множитель cos α и получаем:
d3(ΔQ)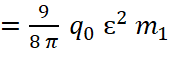
ρ2 R0 sin2α cosα dα
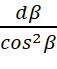dφ
Интегрируя это уравнение по dφ от 0 до 2π, по dβ от -βm до βm и по α от 0 до αm, получаем: ΔQ =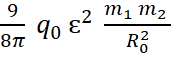 
. Вводя обозначение
ϓ =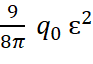 
, (13)
и поскольку F = ΔQ, получаем известную формулу Ньютона:
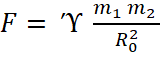. (14)
Не трудно убедиться, что формула Ньютона применима и в случае произвольной формы второго тела при условии, что R0> r1>> l2, где l2 – максимальный линейный размер второго тела. А если расстояние между телами много больше линейных размеров и первого тела, то (14) применимо и в случае произвольной формы обоих тел – они тогда рассматриваются как точечные.
Теперь рассмотрим случай, когда первое тело достаточно массивно, и входную плотность потока для второго тела нужно брать не по (9), а по (8). Действуя аналогично разобранному выше случаю, получаем:
F= (1-3 ψ1)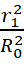 
q₀ ɛ m2. (15)
Внешне это выражение ещё можно привести к виду формулы Ньютона, но с другим значением ϓ:
ϓ1 =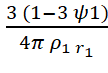 
q₀ ɛ.
Видим, что в данном случае это уже не константа, а функция, зависящая от параметров массивного притягивающего тела.
Некоторые новые результаты
Посмотрим, каким будет ускорение свободного падения, вызываемое сверхмассивным телом. Поделив обе части (15) на m2, получим формулу для ускорения:
gR= (1-3 ψ) q₀ ɛ. (16)
Вблизи поверхности массивного тела, когда R ≈ r, ускорение свободного падения максимально и равно:
g = (1-3 ψ) ɛ q0. (17)
При неограниченном росте массы притягивающего тела неограниченно растёт и величина a=2rɛρ. Зависящая от a величина ψ приобретает неопределённость типа ∞/∞, раскрытие которой даёт ψ=0. Следовательно, максимально возможная величина ускорения свободного падения тела равна:
g m ≈ ɛ q0. (18)
Отсюда видно, что в отличие от теории Ньютона в данной модели тяготения ускорение свободного падения при неограниченном росте массы притягивающего тела не увеличивается безгранично, а стремится к определённому конечному пределу. А наличие конечного предела для ускорения свободного падения означает и ограничения для значений гравитационных сил и энергий, которых нет в теории Ньютона. Ведь в ней формула для гравитационной силы в знаменателе имеет расстояние между центрами притягивающихся тел; при стремлении этого расстояния к нулю значение силы стремится к бесконечности. И для этого не видно каких-то естественных ограничений. Отсюда и возникла идея о существовании чёрных дыр. В предлагаемой здесь теории проблем с бесконечностью просто не возникает. Соответственно исчезает и причина для рассмотрения таких экзотических астрономических объектов как чёрные дыры.
Для получения количественных оценок необходимо определить численные значения коэффициентов ɛ и q0. На первый взгляд, здесь нет проблемы, для этого даже не требуются специальные эксперименты. С помощью (13) выразим q0 через ԑ и ϓ и подставим в (16). Затем после простейших преобразований получаем формулу для вычисления ԑ:
ԑ =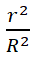 
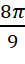
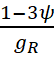ϓ. (19)
Здесь значения ψ являются функцией от a, в свою очередь, a=2 ɛ ρ r, так что значение ԑ имеется и в правой части формулы (19). Само по себе это не создаёт особых трудностей – в таких случаях применяется метод последовательных приближений. Но чтобы получить более или менее достоверное значение искомой величины, должны использоваться данные для достаточно массивного тела. В связи с этим расчёт был проведен с использованием параметров самого крупного тела нашей Солнечной системы – самого Солнца, по которому у нас имеются достаточно надёжные данные. Для расчёта использовались следующие параметры: радиус Солнца r = 7*108 м, ускорение свободного падения бралось на орбите Земли (R = 149,6*109 м) и вычислялось, исходя из её орбитальной скорости 30 км/с; плотность вещества Солнца ρ = 1,42*103 кг/м3. В результате получено значение коэффициента поглощения ԑ = 6*10-14 м2/кг.
Естественно, встаёт вопрос о точности полученной величины, тем более что масса Солнца (а значит и его плотность) получена на основе закона Ньютона, вследствие чего могла возникнуть значительная погрешность. Оценим величину погрешности, которую даёт использование формулы приближённых вычислений (4), заменяющей экспоненциальную зависимость линейной (что приводит к закону Ньютона). Подставляя в (4) значения x = a = 2 ɛ ρ r для Солнца и сравнивая левую и правую части приближённого равенства, можем оценить величину погрешности от линеаризации. В данном случае эта погрешность оказалась относительно небольшой, всего 0,7 % (a ≈ 0,12). Но для космических тел, масса которых в несколько раз превышает солнечную, она уже будет значительной – для тела, у которого a ≈ 0,5, она составит больше 10 %.
Итак, применение закона Ньютона для Солнца при решении связанных с ним гравитационных задач не приводит к большим погрешностям. В ещё большей степени это относится к планетам солнечной системы, поскольку масса даже Юпитера - самой крупной планеты нашей системы, на три порядка меньше массы Солнца. Таким образом, неточности в известном значении массы Солнца не могли привести к большим ошибкам в определении значения коэффициента поглощения. Тем не менее полной уверенности в хорошей точности этого коэффициента нет – всё-таки для его нахождения использовалась формула (19), выведенная для сверхмассивных тел, а расчёт вёлся для Солнца, имеющего массу, при которой ещё возможно применение закона Ньютона.
В этой ситуации, конечно, хотелось бы сравнить полученное здесь значение коэффициента поглощения гравитонов с его значениями, полученными другими исследователями и другими методами. К сожалению, материала в этом плане крайне мало. Конкретные значения данного коэффициента были получены в упоминавшихся выше экспериментах Мажораны. Было проведено две серии опытов. По результатам первой серии было получено значение коэффициента 6,7*10-13 м2/кг, во второй – 2,8*10-13 м2/кг [2, с. 7]. Эксперименты были очень сложными по техническому исполнению и, похоже, не все сложности удалось преодолеть, что сказалось на значительном разбросе полученных результатов. Поэтому рассчитывать на достаточную их точность не приходится.
В. Б. Брагинским, В. Н. Руденко и Г. И. Рукманом были поставлены эксперименты, результатом которых стало доказательство того, что коэффициент поглощения гравитонов меньше 10-13 м2/кг [1, с. 172]. Там же И.И. Кагальникова приводит верхнее значение такого коэффициента, полученное по результатам обработки данных о влиянии поглощения гравитации на морские приливы и равное 1,2*10-16 м2/кг [1, с. 177]. Как видим, полученное здесь значение коэффициента поглощения гравитонов удовлетворяет только первому условию (меньше 10-13 м2/кг). Что касается результатов экспериментов Мажораны, они несколько превышают даже это менее ограничивающее значение. В этой ситуации, по-видимому, наиболее достоверным следует считать полученное здесь значение коэффициента поглощения гравитонов – всё-таки оно получено на основе натурных данных по самому крупному объекту нашей солнечной системы. Из этого и будем исходить.
Определившись со значением ԑ, находим по (13) величину плотности потока импульса гравитонов: q0 = 5,2*1016 кг/ (м с2). Заодно определим ещё один параметр предлагаемой модели – массу (движения) гравитонов, находящихся в каждый момент времени в единичном объёме свободного пространства (n0 µ). Подставляя в (2) значения q0 и с, получаем n0µ = 3,46 кг/м3. Подсчитаем по (18) также величину максимально возможного ускорения свободного падения, оно получается равным gm ≈ 3100 м/с2.
Теперь посмотрим, что ещё нового можно получить, если применить рассматриваемую модель тяготения к сверхмассивным космическим объектам. Возьмём для примера звёзды-гиганты. Считается, что масса самых крупных из них составляет около пятидесяти солнечных, а размеры и светимость больше солнечных в десятки тысяч раз (светимость - до 105 солнечных) [8, с. 603]. Конкретно для примера взято: масса – 50 солнечных (m ≈ 1032 кг), радиус звезды равен r ≈ 45*1010 м (примерно радиус орбиты Марса). При таких параметрах по теории Ньютона ускорение свободного падения на поверхности звезды будет равно g = 3,33*10-2 м/с2. Очевидно, что для реальных космических тел делается наоборот – ускорение свободного падения определяется из наблюдений движения тел, ближайших к рассматриваемому объекту, а массу данного объекта вычисляют, используя закон тяготения. Так что ускорение свободного падения более достоверная величина. Поэтому на основе полученного выше значения g найдём массу звезды, исходя из полученных здесь зависимостей. Для этого по (17) найдём значение ψ, а по нему, используя (6), находим величину a, по ней – плотность ρ. Умножая последнюю на объём звезды, находим её массу. В данном примере получилось: ρ = 6,3 кг/м3 и m = 2,4*1036 кг. Видим, что масса получилась больше исходно принятой примерно на четыре порядка! И это более или менее согласуется со светимостью звезды, вследствие чего этот результат выглядит более правдоподобным. Действительно, если принять массу рассматриваемой звезды равной пятидесяти солнечным, средняя плотность её вещества будет всего 2,6*10-4 кг/м3. Не понятно, какие реакции могут обеспечить высокую светимость звезды при столь низкой плотности вещества?!
Не менее принципиальные отличия между данной моделью гравитации и теорией Ньютона возникают при рассмотрении очень массивных космических тел относительно малых размеров. Возьмём для примера нейтронную звезду. Примем её параметры, как и в [8, с. 610]: масса звезды порядка массы Солнца, её радиус равен 12,6 км, а плотность равна 2,4*1017 кг/м3. Ускорение свободного падения вблизи поверхности такого тела по теории Ньютона будет равно 1,06*1016 м/с2. Это примерно в 3,4*1012 раз больше максимально возможного ускорения по рассматриваемой модели тяготения. Соответственно во столько же раз будут меньше силы тяготения, что ставит под сомнение существование нейтронных звёзд.
Рассмотренные примеры показывают, что применение представленной здесь теории гравитации к решению вопросов астрофизики даёт принципиально иные результаты по сравнению с имеющимися на основе теории Ньютона и её геометрической интерпретации – общей теории относительности Эйнштейна.
О возможностях экспериментальной проверки
Из вышеизложенного следует, что для тел, имеющих форму шара и не слишком массивных, результаты предлагаемой модели и теории Ньютона неплохо совпадают. Однако такого совпадения не будет при отличии формы тел от предельно симметричной шаровой. Посмотрим это на конкретном примере. В [3, с.241] в качестве примера рассмотрена сила, с которой притягивают друг друга два тонких стержня, расположенных вдоль одной прямой. Приведена формула для этой силы:
F = G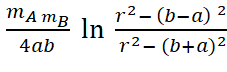 
, (20)
где G – гравитационная постоянная, mA – масса и 2a – длина стержня A; соответственно, mB – масса и 2b – длина стержня B; r – расстояние между центрами масс стержней. Из (20) видно, что при сближении стержней до соприкосновения их торцов значение силы притяжения стержней становится бесконечно большим, так как при этом r= a+b, и знаменатель дроби, от которой берётся логарифм, превращается в нуль. Следовательно, в данном случае теория Ньютона неприменима. Предлагаемая же здесь модель нормально работает и в этом случае – как было показано выше, при её использовании бесконечные значения сил принципиально не могут возникнуть. Ведь значения ускорения свободного падения ограничены величиной gm, а значит, ограничена и величина силы притяжения, равная произведению ускорения на массу рассматриваемого тела. Выводы по рассмотренному примеру можно распространить и на случай цилиндрических тел. Ведь стержень кругового поперечного сечения – это частный случай цилиндра, длина которого много больше радиуса его сечения.
Столь сильные отличия в описании сил притяжения для цилиндрических тел по закону Ньютона и на основе рассматриваемой модели можно использовать для экспериментальной проверки этой модели. Для этого, например, можно использовать схему известного эксперимента Кавендиша, если изменить форму используемых в эксперименте грузов с шаровой на цилиндрическую. В качестве подвешиваемых на коромысле грузов, которые должны быть достаточно лёгкими, нужно использовать очень короткие цилиндры (диски) массой около 1 кг. А на подставках должны устанавливаться цилиндры значительной длины с массой порядка 200 кг или даже больше, если позволят технические возможности эксперимента. Оси диска и цилиндра должны лежать на одной прямой. Если измеренные величины сил окажутся близкими к расчётным, можно считать, что эксперимент подтвердил правильность данной модели.
Чтобы получить расчётные значения сил притяжения в таком эксперименте выведем формулы для плотности потока импульса гравитонов на выходе из торцевой поверхности цилиндрического тела. При этом используем ту же методику, что и в изложенном выше выводе для шарового тела. Отличие только в том, что в данном случае искомая плотность потока будет складываться из двух величин: одна из учёта гравитонов, достигающих выходную торцевую поверхность, пройдя через входную торцевую поверхность, а вторая – из учёта гравитонов, прошедших сначала через боковую поверхность цилиндра.
При этом строгое решение обозначенной задачи (для всех точек выходного торца на произвольном расстоянии от оси цилиндра) оказалось математически довольно сложным, результат не удаётся получить в компактном виде. Поэтому оставим его на потом, когда (если) будет осуществляться подобный эксперимент. На данном этапе достаточно получить качественное решение – пусть менее точное, но зато существенно более простое. Оно заключается в том, что искомая величина определяется только для центральной точки, лежащей на оси цилиндра, где условия симметрии значительно упрощают задачу. И при расчёте плотности выходящего потока она используется как средняя для всей площади выходного торца цилиндра. Расчётная схема для данного случая приведена на рис.4.
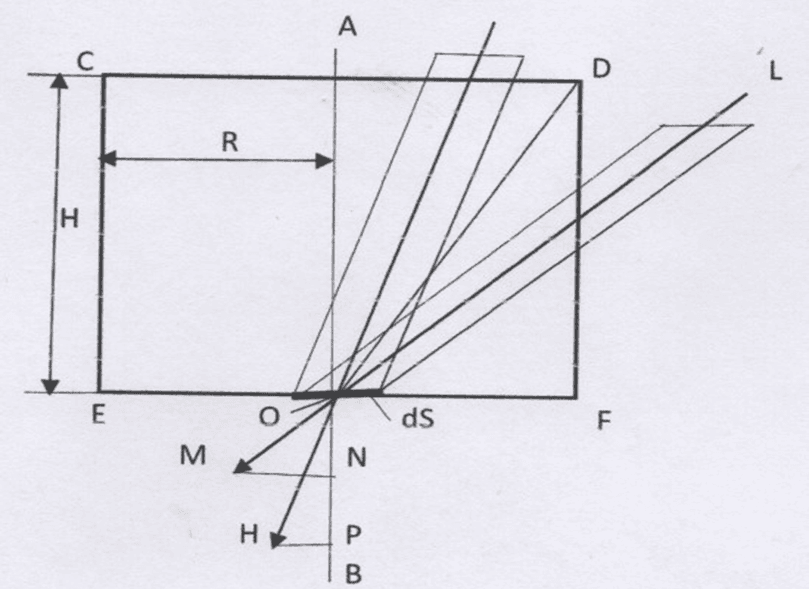
Рис. 4
Поскольку методика вывода интересующей нас зависимости принципиально та же, что и для шара, опуская вывод, приводим сразу полученное выражение для плотности потока импульса гравитонов на выходе из цилиндрического тела в направлении его оси:
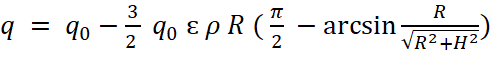. (21)
Таким образом, на диск, приближаемый к цилиндру практически до соприкосновения, со стороны цилиндра будет воздействовать плотность потока импульса гравитонов, определяемая по (21), а с противоположной стороны - плотность потока равна q0. Их разность Δq = q0 - q обусловливает возникновение силы притяжения
F = Δq ɛ ρ δ S = Δq ɛ m,
где δ, S и m – толщина, площадь торцевой поверхности и масса диска.
В итоге имеем:
.
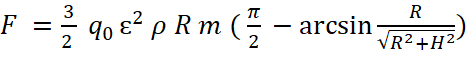Или, если ɛ2 выразить из (13) через ϒ:
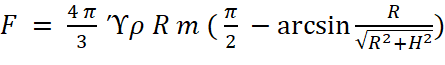. (22)
Точность расчёта будет выше, если радиус диска принимать в разы меньше радиуса цилиндра. Однако здесь нужна мера. Ведь при этом, чтобы не уменьшать и без того малую массу диска, придётся увеличивать его толщину. И из диска может получиться небольшой цилиндр, в который через его боковую поверхность будут попадать гравитоны, прошедшие перед этим через первый (большой) цилиндр, что не учитывается предлагаемой схемой расчёта.
Рассмотрим конкретный пример. Чтобы было с чем сравнивать получаемые результаты, примем массы тел, рассматриваемых в этом примере (цилиндра и диска), примерно равными массам большого и малого шаров в эксперименте Кавендиша (158 кг и 0,729 кг [3, с. 243]). Пусть радиус цилиндра будет равным 12,1 см при его длине 30 см, а радиус диска – 5 см при толщине 0,8 см; их массы при этом будут соответственно 158 кг и 0,716 кг (материал, как и в эксперименте Кавендиша – свинец). Параметры цилиндра приняты таковыми из тех соображений, что при заданной массе цилиндра принятое соотношение между радиусом цилиндра и его длиной соответствует примерно максимальному значению силы притяжения по (22). В результате сила притяжения между цилиндром и диском в момент, близкий к соприкосновению, получилась для одной пары тел равной 33*10-8 Н, т.е. того же порядка, что и в эксперименте Кавендиша (там было примерно 25*10-8 Н). Результат правдоподобный, и никаких бесконечностей!
При значительном увеличении длины цилиндра при неизменной массе точность формулы (22) возрастает за счёт того, что при этом относительная разность путей прохождения гравитонов в цилиндре (где происходит поглощение) у гравитонов, выходящих затем из цилиндра по его оси и гравитонов, выходящих на различных расстояниях от неё, уменьшается. Правда, при этом уменьшается и сила притяжения. В приведенном выше примере был рассмотрен предельный случай увеличения длины цилиндра до того, что его радиус уменьшился до радиуса диска. При этом длина цилиндра стала равной 1,76 м. То есть, по существу, уже получился стержень. Сила притяжения в этом случае оказалась равной 18*10-8 Н, т.е. получилась почти вдвое меньше. Но порядок величины остался тем же. Так что можно рассмотреть и этот вариант для использования в эксперименте по проверке предложенной здесь новой теории.
Отметим, что q0 здесь полагалось величиной постоянной. Ведь за сотни лет наблюдений за движением космических тел не замечено малейших изменений в закономерностях их движений. Но вполне возможно, что в очень далёком прошлом и будущем, а также в участках вселенной, отстоящих от нас на миллионы световых лет, значения q0 могут быть иными. Не рассматривалось здесь и влияние конечности скорости распространения носителей поля гравитации.
Выводы
- Модель гравитации Лесажа с учётом современных знаний об элементарных частицах явилась хорошей основой для разработки теории гравитации, более общей, чем теория Ньютона, вошедшая в неё как частный случай.
- Результаты обеих теорий практически совпадают для не слишком массивных по космическим масштабам тел, имеющих форму шара, а также если взаимодействующие тела можно считать точечными, т.е. размерами которых можно пренебречь по сравнению с расстоянием между ними.
- Применение закона тяготения Ньютона к объектам солнечной системы даёт достаточно точные результаты. Только для самого Солнца, в котором сосредоточена большая часть массы системы, возникают погрешности около одного процента. А применение закона Ньютона к объектам, масса которых в несколько раз больше, чем у Солнца, и параметр a = 2 ɛ ρ r равен примерно 0,5 (для Солнца он равен 0,12) даёт погрешность более 10%.
- Принципиально новые результаты получаются в результате применения рассмотренной здесь модели гравитации к сверхмассивным объектам астрофизики. В частности, выявлено наличие верхнего предела ускорения свободного падения в поле тяготения тел сколь угодно большой массы, а также что массы звёзд-гигантов оказываются на много порядков больше рассчитанных по теории Ньютона. С позиции данной модели вызывает сомнение существование нейтронных звёзд и совершенно не видно места для чёрных дыр.
- Для тел небольшой массы и имеющих форму, отличную от шаровой, при расстояниях между телами, сопоставимыми с их линейными размерами, закон Ньютона может давать явно неверные значения для сил тяготения, вплоть до бесконечно больших. Этого нет в предложенной здесь модели тяготения, что можно использовать для экспериментальной проверки данной модели.
