Задание №10 по теме «Графики функций» ЕГЭ по математике профильного уровня 2023 года

Задача на тему “Графики функций” в едином государственном экзамене по математике профильного уровня появилась только в 2022 году, на данный момент это самая молодая и мало изученная задача на экзамене.

В перечне требований к результатам освоения основной образовательной программы среднего общего образования указано, что для успешного выполнения этой задачи экзаменуемый должен уметь:

• определять значение функции по значению аргумента при различных способах задания функции; описывать по графику поведение и свойства функции, находить по графику функции наибольшее и наименьшее значения; строить графики изученных функций, описывать с помощью функций различные реальные зависимости между величинами и интерпретировать их графики;
• моделировать реальные ситуации на языке алгебры, составлять уравнения и неравенства по условию задачи; исследовать построенные модели с использованием аппарата алгебры, а именно – решать уравнения, простейшие системы уравнений, используя свойства функций и их графиков; использовать для приближенного решения уравнений и неравенств графический метод;

В перечне элементов содержания, проверяемых на едином государственном экзамене по математике задачей на тему “Графики функций” указаны:

• Линейная функция, её график
• Функция, описывающая обратную пропорциональную зависимость, её график
• Квадратичная функция, её график
• Степенная функция с натуральным показателем, её график
• Тригонометрические функции, их графики
• Показательная функция, её график
• Логарифмическая функция, её график

А также преобразования графиков функций: сдвиг, умножение на число, отражение относительно координатных осей.

Количество заданий по теме графики функций, представленных на сайте fipi.ru [2] в открытом банке задач, на данный момент невелико, поэтому при подготовке к экзамену мы можем дополнительно использовать задачи из сборников, рекомендованных ФИПИ [1], варианты ЕГЭ, тренировочных [3] и диагностических работ этого и прошлого года и собственную фантазию.

Примерное время выполнения задания выпускником, изучавшим математику на профильном уровне, 8 минут.

Перейдём к разбору задач. Первая группа из трёх заданий решается подстановкой координат единственной точки в указанную функцию, получением недостающего параметра и вычислением искомого значения.

Задача 1. На рисунке 1 изображён график функции вида 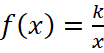. Найдите значение f(10).

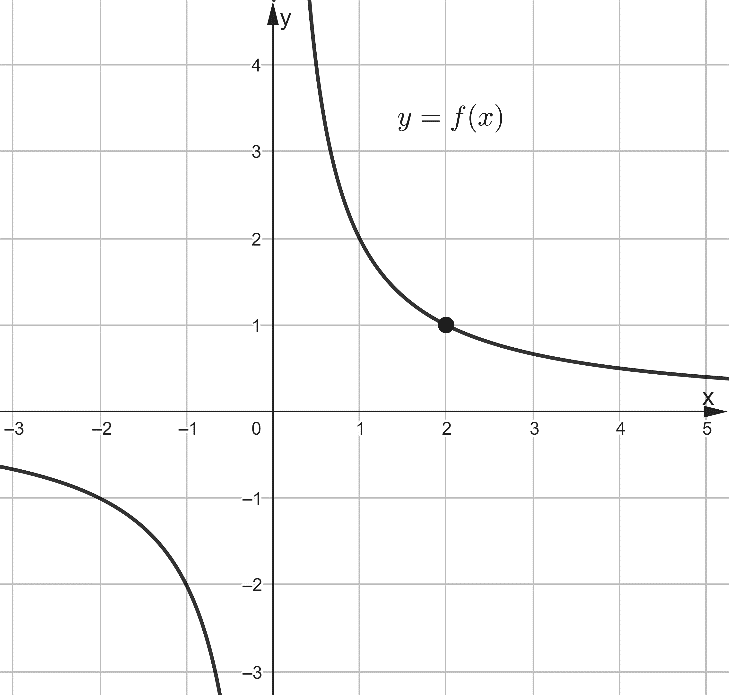
Рис. 1

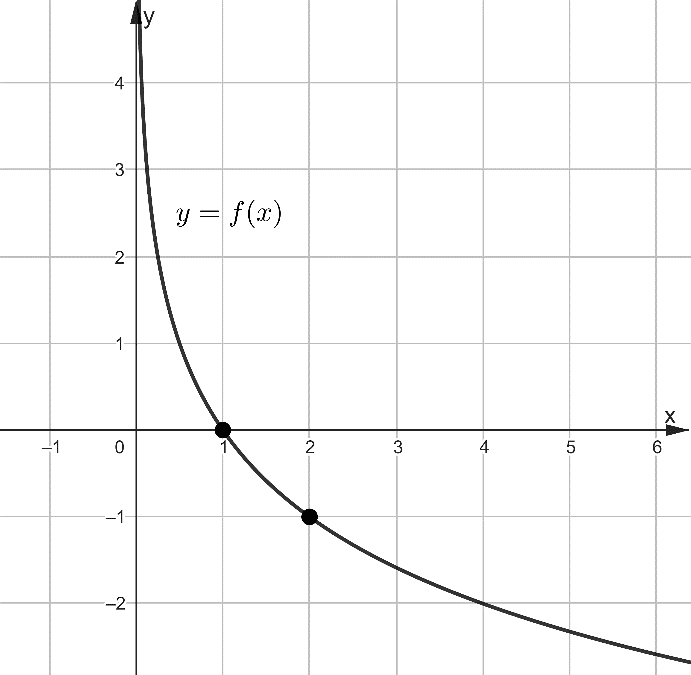
Рис. 2

Решение: Координаты точки, указанной на рисунке, (2;1), подставляем в равенство, получаем 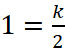 или k=2, значит, изображённая функция имеет вид  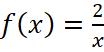 а .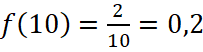

Ответ: 0,2.

Задача 2. На рисунке 2 изображён график функции вида 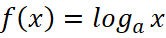. Найдите значение переменной, при которой f(x)=-4.

Решение: На приведённом рисунке указаны две точки, координаты первой (1;0) не позволяют найти значения параметра a, так как все логарифмические функции данного вида проходят через эту точку. Подставляя в равенство координаты второй точки (2;-1), получаем 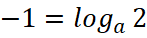 или 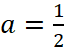, значит, изображённая функция имеет вид  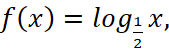а f(x)=-4, если  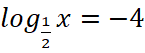или x=16.

Ответ: 16.

Задача 3. На рисунке 3 изображён график функции вида 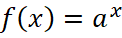. Найдите значение f(-3).

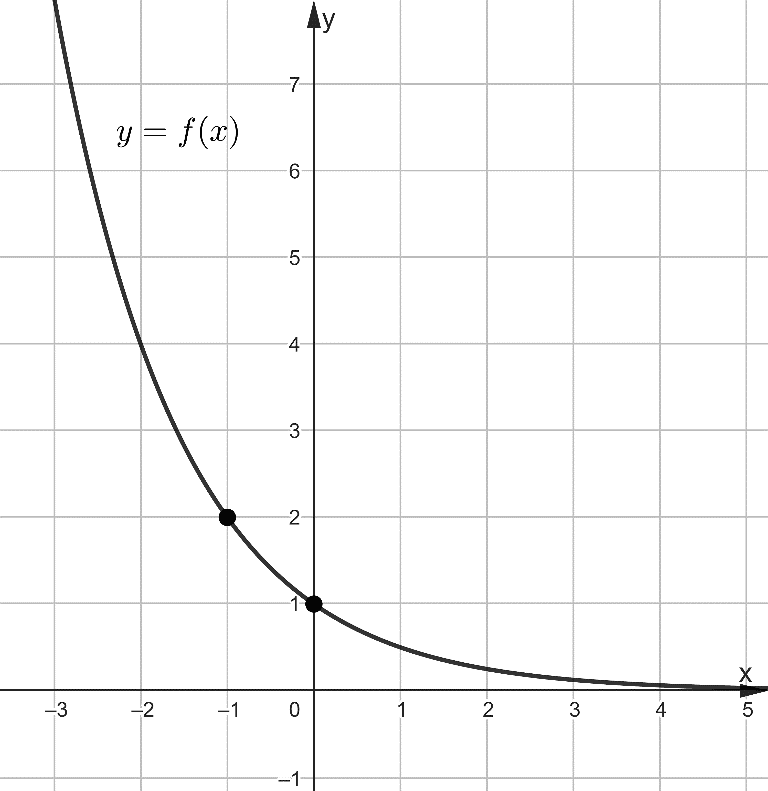
Рис. 3

Решение: На приведённом рисунке указаны две точки, координаты первой (0;1) не позволяют найти значения параметра a, так как все показательные функции данного вида проходят через эту точку.

Подставляя в равенство координаты второй точки (-1;2), получаем 2=a^-1 или 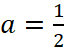, значит, изображённая функция имеет вид 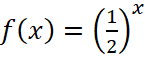, а 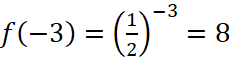. Ответ: 8.

В следующей группе задач будут рассмотрены линейные функции, напомним основные сведения о них.

Линейную функцию можно задать уравнением с угловым коэффициентом y=kx+b, где коэффициент k отвечает за угол наклона α прямой к оси O_x (рис.4).

В случае когда свободный коэффициент b равен нулю, функция превращается в прямую пропорциональность y=kx, если нулю равен угловой коэффициент k, то графиком функции будет горизонтальная прямая y=b (рис.5).

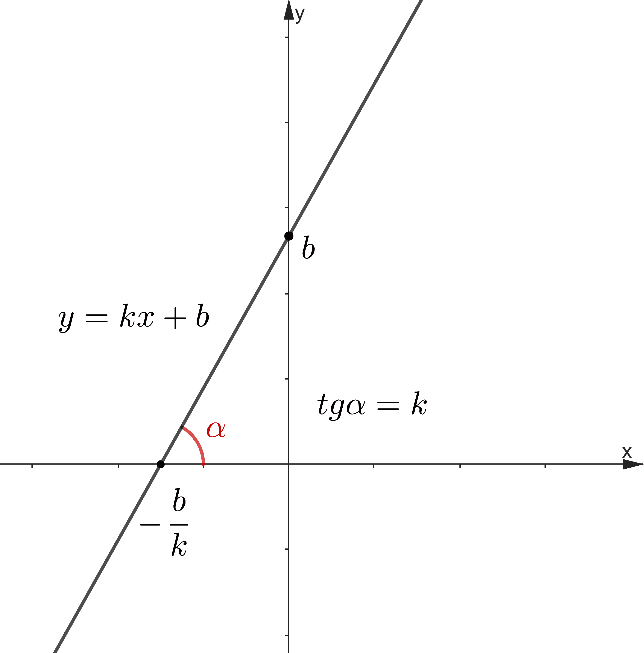
Рис. 4

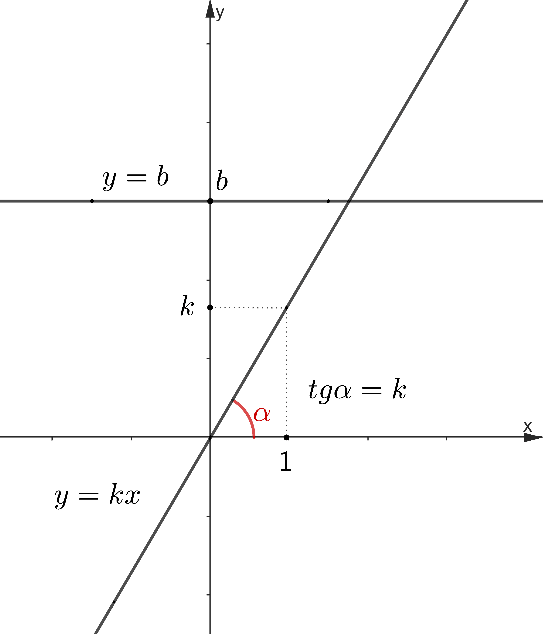
Рис. 5

Следует напомнить, что существует ещё один способ задания линейной функции, эффективный на ЕГЭ, – это уравнение прямой, проходящей через две точки с координатами (x₁;y₁) и .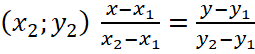

Задача 4. На рисунке 6 изображён график функции вида f(x)=kx+b. Найдите значение f(5).

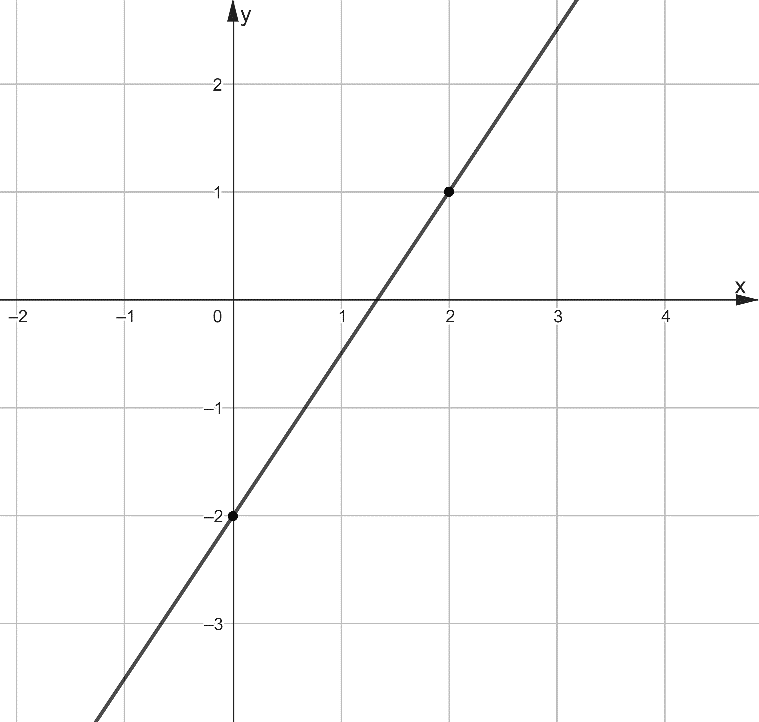
Рис. 6

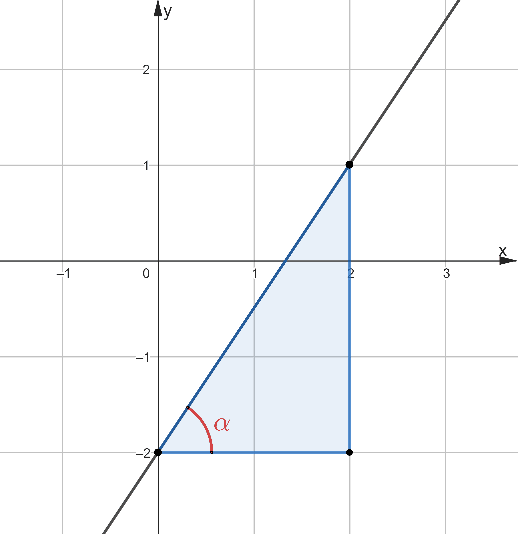
Рис. 7

Решение: Способ 1. Определим координаты выделенных точек A(2;1)  и B(0;-2). Самым простым способом решения задачи является подстановка координат выделенных точек в функцию и решение полученной системы уравнений 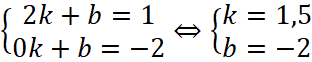. Следовательно, на рисунке изображён график функции y=1,5x-2, а f(5)=1,5⋅5-2=5,5.

Способ 2. Построив вспомогательный прямоугольный треугольник (рис.7), проходящий через две выделенные точки, получим, что тангенс угла наклона прямой к оси O_x равен 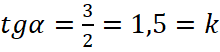, а прямая пересекает ось O_y в точке с ординатой равной b, значит, b=-2, следовательно, на рисунке изображён график функции y=1,5x-2, а f(5)=1,5⋅5-2=5,5.

Способ 3. Воспользуемся уравнением прямой, проходящей через две точки и подставим в него координаты выделенных точек A(2;1) и B(0;-2), через которые проходит наша прямая. Получим, что 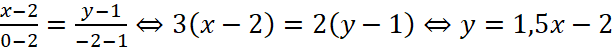. Ответ: 5,5.

Задача 6. На рисунке 8 изображён график функции вида f(x)=kx+b. Найдите сумму коэффициентов k и b.

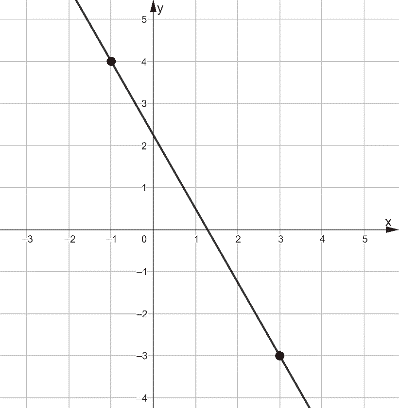
Рис. 8

Решение: Эту задачу опять можно решить подстановкой двух точек в исходную функцию или с помощью уравнения прямой, проходящей через две точки. При решении с помощью нахождения тангенса угла наклона (рис.9) могут возникнуть трудности, связанные с тем, что ученики неверно находят угол α между прямой и осью O_x, путая его со смежным углом β.

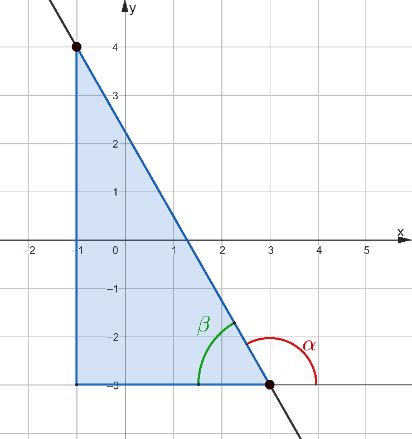
Рис. 9

, .

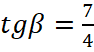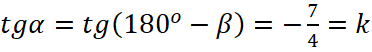Коэффициент b можно найти, подставив координату одной из точек, например (-1;4), в уравнение 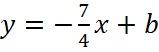. Получаем 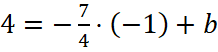или 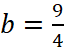, тогда 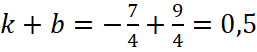. Ответ: 0,5.

Задача 7. На рисунке 10 изображены графики двух линейных функций, пересекающиеся в точке A. Найдите абсциссу точки A.

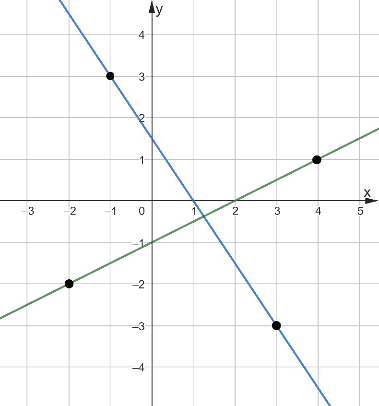
Рис. 10

Решение: Уравнения линейных функци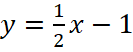й  и 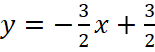, абсцисса точки пересечения x=1,25.

Ответ: 1,25.

Перейдём к задачам на квадратичную функцию.

Задача 8. На рисунке 11 изображён график функции вида 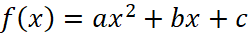. Найдите значение f(-6).

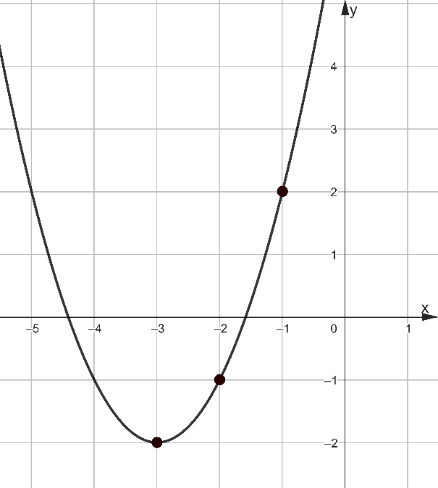
Рис. 11

Решение: у этой задачи опять существует несколько способов решения, ученикам с минимальным уровнем знаний о квадратичной функции проще будет воспользоваться первым способом, а более продвинутым школьникам – последующими.

Способ 1. Найдём координаты выделенных точек (-3;-2), (-2;-1) и (-1;2) и решим систему, подставив их в уравнение функции. 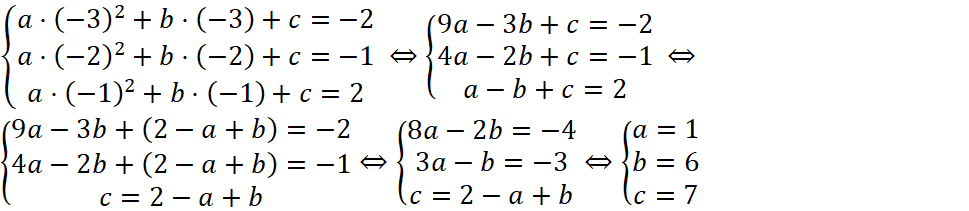, , 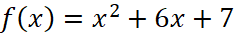а .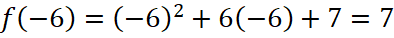

Способ 2. Для решения задачи можно использовать значение абсциссы вершины параболы 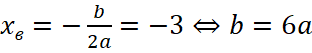 и подставить только две точки в функцию 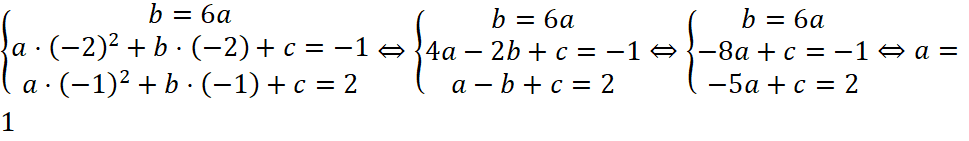, b=6, c=7. При таком способе решения системы решается несколько быстрее и выглядит менее громоздко.

Способ 3. Этот способ подойдёт для школьников, которые знакомы с элементарными преобразованиями графиков функций, претендует на высокие баллы за экзамен и хочет потратить на решение задачи минимум времени.

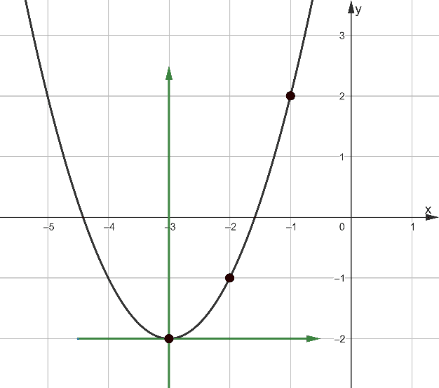
Рис. 12

Введём вспомогательную систему координат с центром в вершине параболы (рис.12) и заметим, что в новой системе координаты точек равны (0;0), (1;1) и (2;4), то есть в новой системе координат эта парабола задаётся уравнением y=x².

Из этого мы можем сделать вывод, что график искомой функции получается линейными преобразованиями квадратичной функции y=x², а именно сдвигом на 3 единицы влево и на 2 вниз, то есть искомая функция имеет вид 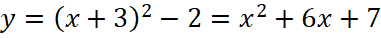, а f(-6)=7.

Ответ: 7.

Задача 9. На рисунке 13 изображён график функции вида 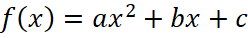. Найдите значение c.

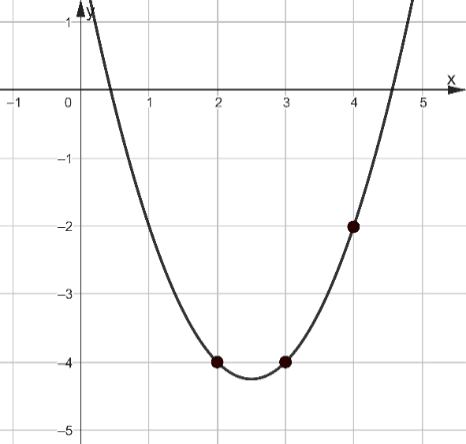
Рис. 13

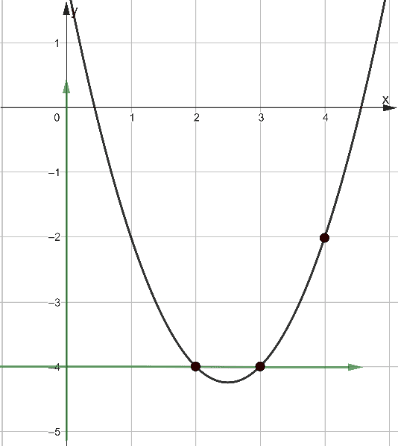
Рис. 14

Решение: Этот номер можно решать подстановкой трёх точек в уравнение функции, а можно опять ввести вспомогательную систему координат (рис.14), в которой у параболы будут два пересечения с осью O_x – точки 2 и 3. Следовательно, квадратичная функция в новой системе координат описывается равенством y=a(x-2)(x-3). Подставив точку (4;2) получим, что a=1. А далее, легко видеть, что искомый график получается из графика y=(x-2)(x-3) сдвигом на 4 по вертикали, то есть уравнение имеет вид y=(x-2)(x-3)-4 или y=x²-5x+2, значит, c=2.

Ответ: 2.

Задача 10. На рисунке 15 изображены графики функций видов f(x)=2x²-5x+5 и g(x)=ax²+bx+c, пересекающиеся в точкаx A и B. Найдите ординату точки B.

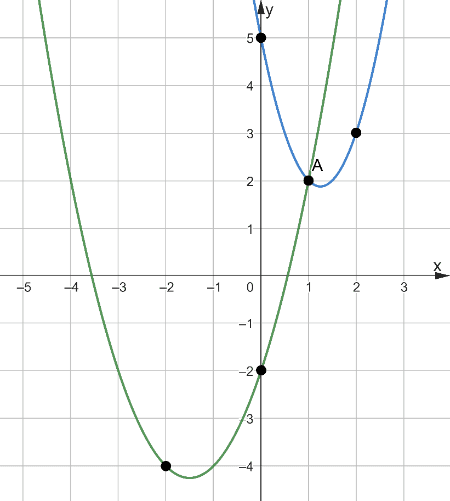
Рис. 15

Решение: При решении этой задачи учащиеся сталкиваются с двумя проблемами: не все школьники могут сопоставить функции и их графики, и не все школьники понимают где расположена точка B, так как она не указана на рисунке.

Задача о сопоставлении графиков быстро решается нахождением вершины параболы, заданной уравнением f(x)=2x²-5x+5, абсцисса её вершины 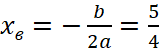, значит, график функции y=f(x) расположен справа. Находим коэффициенты a, b и c для функции y=g(x) и получаем, что g(x)=x²+3x-2.

Для того, чтобы найти точки пересечения двух функций, нужно решить систему уравнений 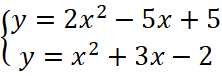. Решениями системы являются две пары чисел (1;2) и (7;68), первая пара является координатами точки A, изображенной на рисунке, значит, второе решение соответствует координатам точки B, ордината которой равна 68.

Ответ 68.

Задача 11. На рисунке 16 изображён график функции вида f(x)=ax²+bx+c. Найдите произведение абсцисс точек, для которых f(x)=-13.

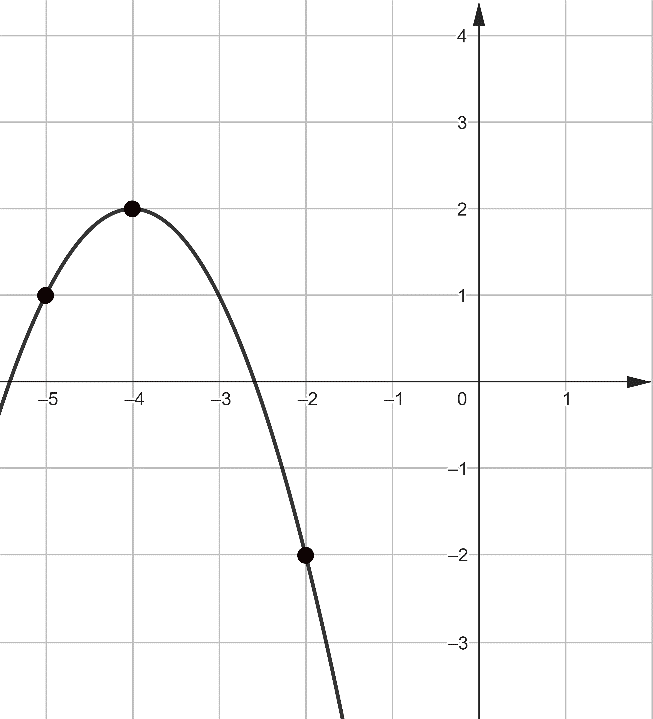
Рис. 16

Решение: Находим коэффициенты a, b и c для функции y=f(x) и получаем, что f(x)=-x²-8x-14.

Для того, чтобы найти абсциссы точек, при которых f(x)=-13, нужно решить уравнение -x²-8x-14=-13⇔x²+8x+1=0. Произведение корней уравнения находится по теореме Виета и равно .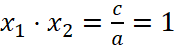

Ответ: 1.

Успешному решению задач на графики дробно-рациональных функций помогает знание того, что график функции 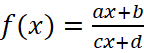 имеет две асимптоты: вертикальную  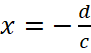и горизонтальную 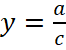, к которой график функции стремится при x→∞. График дробно-рациональной функции вида 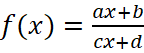симметричен относительно точки пересечения асимптот.

Задача 12. На рисунке 17 изображён график функции вида 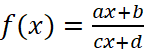. Найдите значение f(6).

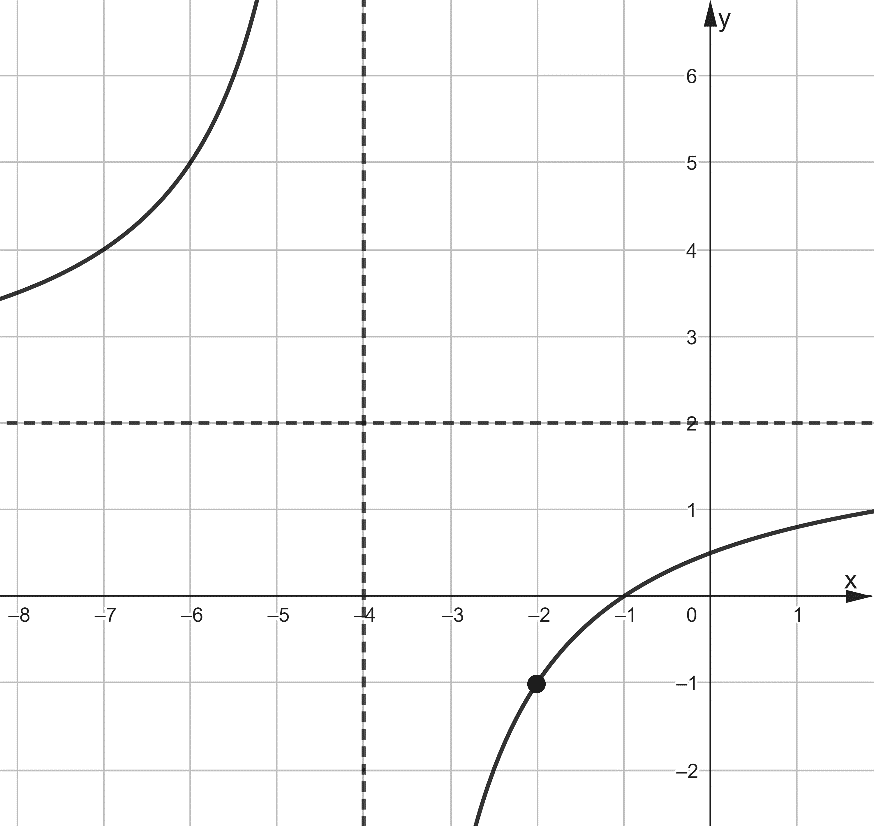
Рис. 17

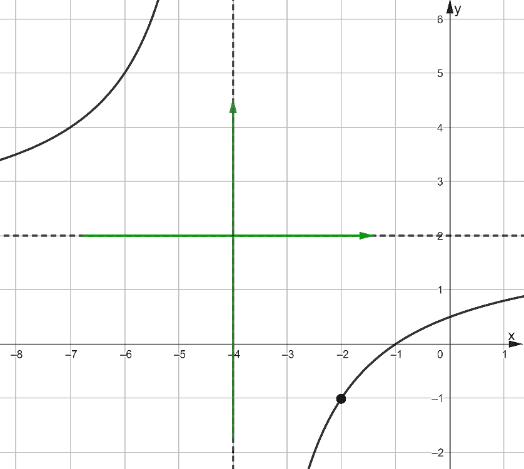
Рис. 18

Решение: Способ 1. График функции 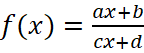имеет две асимптоты: вертикальную  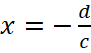и горизонтальную 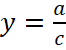, получаем что  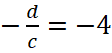 и 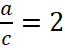, откуда d=4c и a=2c. Из рисунка видно, что график функции проходит через точку (-2;-1). Подставив всю известную информацию в уравнение функции, получим 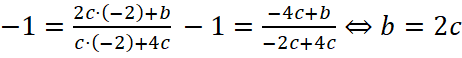, следовательно, 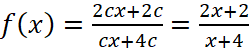, а .

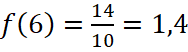Способ 2: Введём новую систему координат, так что оси будут направлены вдоль асимптот исходной функции (рис.18).

В этой системе координат наш график является графиком обратной пропорциональности 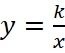. В новой системе координат график проходит через точку с координатами (2;-3), значит 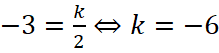, получаем .

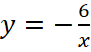График искомой функции получается линейными преобразованиями функции 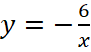, а именно сдвигом на 4 единицы влево и на 2 вверх, то есть искомая функция имеет вид 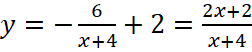, а .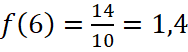

Ответ: 1,4.

Задача 13. На рисунке 19 изображён график функции вида 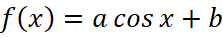. Найдите значение a.

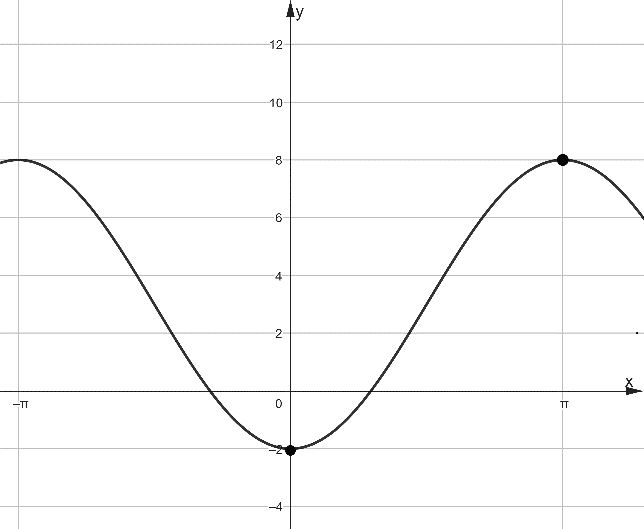
Рис. 19

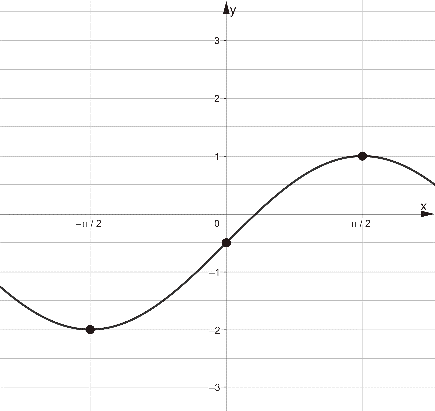
Рис. 20

Решение: Способ 1. Найдём координаты точек, через которые проходит график функции, (0;-2), (π;8) и решим систему, подставив их в уравнение функции 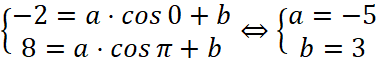, значит, искомая функция имеет вид .

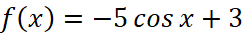Способ 2. Коэффициент a у искомой функции отвечает за сжатие-растяжение графика функции вдоль оси O_y. Мы видим, что амплитуда у графика, изображённого на рисунке, равна 10 и делаем вывод, что 2|a|=10, то есть a=5 или a=-5, чтобы выбрать нужное значение, заметим, что в точке 0 у изображённой функции достигается минимальной значение, тогда как у обычной функции y=cosx точка 0 является точкой локального максимума, значит, график был не только растянут вдоль оси O_y, но и симметрично отражён относительно оси O_x, а коэффициент a=-5. Последнее преобразование графика – сдвиг на 3 вверх, значит, искомая функция имеет вид 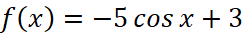. Ответ: -5.

Задача 14. На рисунке 20 изображён график функции вида 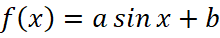. Найдите значение.

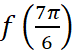Решение: График искомой функции – синусоида, растянутая в 1,5 раза и сдвинутая на 0,5 вниз, то есть функция имеет вид 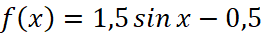, 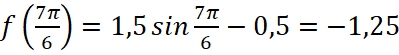. Ответ: -1,25.

Мы видим, что для успешного решения задач на тему “Графики функций” учащийся должен не только быть знакомым с графиками элементарных функций, а ещё и моделировать реальные ситуации на языке алгебры, составлять уравнения и системы уравнений по условию задачи; исследовать построенные модели с использованием аппарата алгебры, быть знакомым с элементарными преобразованиями графиков функций.