Модификации алгоритма Дейкстры для поиска кратчайшего пути

Актуальность исследования

Исследования по модификациям алгоритма Дейкстры для поиска кратчайшего пути остаются актуальными и востребованными. Алгоритм Дейкстры является одним из основных и широко применяемых алгоритмов для решения задач на графах, включая поиск кратчайшего пути во многих приложениях, таких как маршрутизация сетевых пакетов, планирование маршрутов в транспортных системах, оптимизация процессов и т.д.

Однако классический алгоритм Дейкстры имеет свои ограничения и предполагает наличие неотрицательных весов ребер в графе. В реальных приложениях часто возникают ситуации, когда ребра могут иметь отрицательные веса или когда важны дополнительные ограничения и факторы, которые нужно учесть при поиске кратчайшего пути.

Цель исследования

Целью исследования является проведение анализа новых подходов, модификаций или улучшений алгоритма Дейкстры с целью расширения его возможностей, учета дополнительных ограничений или повышения его эффективности.

Материал и методы исследования

Изучением вопросов, посвященных модификации алгоритма Дейкстры, занимались такие ученые как А.Н. Назаров, К.И. Сычев, Ю.Ю. Громов, В.О. Драчев, К.А. Набатов, О.Г. Иванова, Р.Л. Михайлов и др.

Методами исследования являются: теоретический анализ, эмпирические эксперименты, математическое моделирование, сравнительный анализ.

Результаты исследования

Модифицированный алгоритм Дейкстры для поиска кратчайших путей между вершинами графовой модели функциональных блоков представляет собой важную технику в области информационных технологий. Этот алгоритм позволяет эффективно оптимизировать процесс поиска кратчайшего пути в неориентированных взвешенных графах с единичной длиной ребра.

Одна из основных особенностей модифицированного алгоритма Дейкстры заключается в том, что он исключает уже найденные на предыдущем этапе конечные числовые метки из процесса сложений и сравнений. Это значительно сокращает количество операций, улучшая производительность алгоритма.

Алгоритм Дейкстры является одним из основных алгоритмов для нахождения кратчайшего пути в графе. Однако существуют некоторые модификации и оптимизации этого алгоритма. Можно выделить несколько из них.

1. Очередь с приоритетом на базе кучи (Heap-based Priority Queue). Алгоритм Дейкстры требует постоянного обновления приоритета вершин в процессе выполнения. Использование очереди с приоритетом, реализованной на базе кучи (например, двоичной кучи или Фибоначчиевой кучи), позволяет эффективно обрабатывать операции вставки и извлечения элементов с наименьшим приоритетом.
2. Ограничение числа релаксаций (Relaxation Count Limit). В некоторых случаях, особенно при работе с большими графами, можно ограничить число релаксаций для каждой вершины. Это может привести к быстрому завершению алгоритма и уменьшению общего времени выполнения.
3. Использование более эффективной структуры данных. Вместо использования обычного массива или списка для хранения графа, можно применить более эффективную структуру данных, такую как разреженная матрица смежности или список смежности. Это позволит сократить время доступа к соседним вершинам и улучшить производительность алгоритма.
4. Параллельная реализация. Алгоритм Дейкстры можно эффективно распараллелить на множество потоков или процессов, чтобы ускорить его выполнение. Различные вершины могут быть обработаны независимо друг от друга, что позволяет снизить общее время работы.
5. Двунаправленный поиск (Bidirectional Search). Вместо применения алгоритма Дейкстры от начальной вершины до целевой вершины, можно выполнить два поиска одновременно: один от начальной вершины к цели и один от цели к начальной. Как только эти два поиска встретятся, можно найти кратчайший путь. Это может существенно сократить количество релаксаций и улучшить производительность алгоритма [1, c, 103].
6. Алгоритм Дейкстры с ограничением на расстояние (Dijkstra’s Algorithm with Distance Constraint). Вместо нахождения кратчайшего пути до всех вершин в графе, можно ограничиться поиском кратчайшего пути до вершин, находящихся на заданном расстоянии от исходной вершины. Это может быть полезно, когда требуется найти пути только до ближайших вершин, что позволяет сократить количество операций и ускорить выполнение алгоритма.
7. Алгоритм Дейкстры с использованием двоичной кучи и улучшенным обновлением приоритета (Dijkstra’s Algorithm with Binary Heap and Improved Priority Update). Вместо обычной операции обновления приоритета, можно применить улучшенную версию, которая избегает дублирования элементов в очереди с приоритетом. При обновлении приоритета вершины ее новое значение приоритета помещается в очередь, и только если новое значение меньше предыдущего. Это позволяет снизить количество операций и повысить эффективность алгоритма.
8. Алгоритм Дейкстры с использованием отсечения (Dijkstra’s Algorithm with Pruning). Во время выполнения алгоритма некоторые вершины могут быть отсечены из рассмотрения на основе определенных условий или эвристических оценок. Например, можно отсечь вершины, расстояние до которых превышает некоторую верхнюю границу. Это позволяет сократить количество вершин, которые нужно обрабатывать, и ускорить выполнение алгоритма.
9. Алгоритм Дейкстры с учетом стоимости ребер и времени (Dijkstra’s Algorithm with Edge Cost and Time Consideration). В некоторых ситуациях, помимо стоимости ребер, также может быть важно учитывать время, необходимое для прохождения ребра. В этом случае, при выборе следующей вершины для посещения, можно учитывать, как стоимость ребра, так и время, чтобы оптимизировать кратчайший путь с учетом обоих факторов.

Реализацию алгоритма Дейкстры в области информационных технологий можно представить в виде схемы (рисунок).

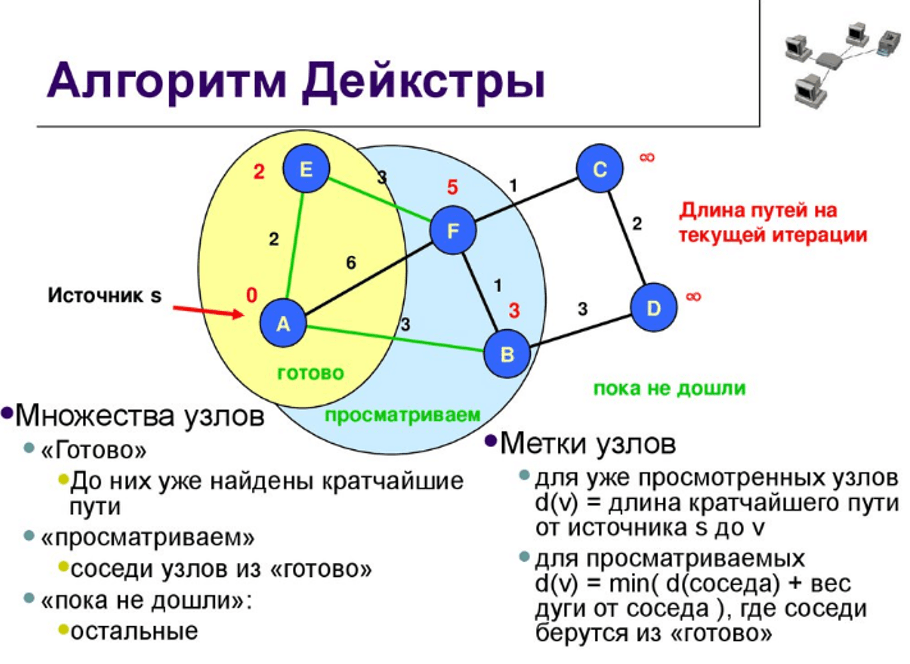
Рис. Механизм реализации алгоритма Дейкстры в IT сфере

В информационных технологиях при использовании модификаций алгоритма Дейкстры для поиска кратчайшего пути могут возникать некоторые проблемы. Можно выделить несколько из них и возможные пути их решения:

1. Сложность работы с большими графами. При работе с графами большого размера обычный алгоритм Дейкстры может быть слишком медленным и требовать значительных вычислительных ресурсов. Для решения этой проблемы можно применить оптимизации, такие как использование разреженной структуры данных для представления графа, распараллеливание алгоритма, а также применение ограничений и эвристик для сокращения количества вершин, которые нужно рассматривать.
2. Обработка отрицательных весов ребер. Алгоритм Дейкстры не может корректно работать с графами, содержащими отрицательные веса ребер. В таких случаях можно применить модификацию алгоритма, такую как алгоритм Беллмана-Форда или алгоритм Дейкстры с ограничением на количество итераций, которые способны обнаружить отрицательные циклы и предотвратить зацикливание [2, c. 273].
3. Неоднозначность пути с равными весами ребер. Если в графе существуют ребра с одинаковыми весами, алгоритм Дейкстры может найти несколько различных кратчайших путей. Если требуется найти только один из них, можно применить дополнительные эвристики или правила выбора пути, такие как предпочтение определенного направления или выбор случайного пути.
4. Эффективность обновления приоритетов. Обновление приоритетов вершин в очереди с приоритетом может быть затратной операцией. Для улучшения эффективности можно использовать улучшенные структуры данных, такие как Фибоначчиева куча, которая позволяет выполнять операции обновления приоритетов за константное время.
5. Недоступность определенных вершин. Если в графе имеются недоступные вершины или ребра, которые невозможно пройти, алгоритм Дейкстры может продолжать их рассматривать и выполнять лишние операции [3, c. 181].
6. Циклы в графе. Если в графе есть циклы, алгоритм Дейкстры может зациклиться, так как он не предусматривает обработку циклов. Одним из путей решения этой проблемы является применение алгоритма Дейкстры с ограничением на количество итераций, чтобы избежать бесконечной обработки циклов.
7. Несвязный граф. Если граф не является связным, алгоритм Дейкстры может не найти путь до некоторых вершин. Для решения этой проблемы можно проверить связность графа перед запуском алгоритма или использовать модификации, такие как алгоритм Дейкстры с ограничением на расстояние, чтобы найти пути только до ближайших вершин.
8. Выбор оптимальной модификации. В зависимости от конкретной задачи и свойств графа, определенная модификация алгоритма Дейкстры может быть более эффективной. Выбор оптимальной модификации может потребовать экспериментов и анализа производительности для конкретного случая.
9. Сложность времени выполнения. Некоторые модификации алгоритма Дейкстры могут иметь более высокую сложность времени выполнения в сравнении с базовым алгоритмом. При выборе модификации следует учитывать требования к производительности и масштабируемости системы.

Можно представить затраты (время выполнения в худшем случае) различных реализаций алгоритма Дейкстры. При соответствующих реализациях очередей с приоритетами алгоритм выполняется за линейное время (пропорциональное V² для насыщенных сетей и пропорциональное E для разреженных сетей), за исключением очень разреженных сетей.

Таблица

Трудоемкость реализаций алгоритма Дейкстры

Название алгоритм Дейкстры обычно используется для обозначения как абстрактного метода построения SPT пошаговым добавлением вершин в порядке их расстояния от истока, так и его реализации в виде алгоритма со временем выполнения, пропорциональным V2, для представления матрицей смежности, поскольку Дейкстра представил и то, и другое в своей статье, опубликованной в 1959 г. (а также показал, что этим методом можно вычислить и MST) [4, c. 94].

Можно выделить следующие основные механизмы, которые часто используются при модификации алгоритма Дейкстры для поиска кратчайшего пути в компьютерных приложениях:

1. Использование очереди с приоритетом. Для эффективного выбора вершин с наименьшим приоритетом (т.е. минимальным расстоянием до текущей вершины), в модифицированном алгоритме Дейкстры обычно применяют очередь с приоритетом. Это позволяет выбирать и обрабатывать вершины в порядке их приоритетов, снижая сложность времени выполнения алгоритма.
2. Релаксация ребер. Основной шаг алгоритма Дейкстры – релаксация ребер. В процессе релаксации алгоритм обновляет расстояние до смежных вершин, если новый путь оказывается короче текущего. Релаксация выполняется для каждого ребра, выходящего из текущей вершины, и может быть адаптирована в соответствии с конкретной модификацией алгоритма.
3. Проверка посещенных вершин. Для избежания повторного посещения вершин и зацикливания алгоритма, модифицированный алгоритм Дейкстры должен отслеживать посещенные вершины. Это можно осуществить с помощью массива или структуры данных, где для каждой вершины хранится информация о ее посещении.
4. Учет ограничений и эвристик. Различные модификации алгоритма Дейкстры могут учитывать дополнительные ограничения или эвристики для нахождения кратчайшего пути. Например, ограничения на расстояние, ограничения на количество релаксаций или использование эвристических оценок для приоритизации вершин.
5. Обновление приоритетов. В процессе выполнения алгоритма Дейкстры могут возникать необходимость обновления приоритетов вершин в очереди с приоритетом. Это может происходить при нахождении более короткого пути к вершине или при использовании эвристик для изменения приоритетов. Обновление приоритетов требует эффективной реализации в соответствии с выбранной структурой данных для очереди с приоритетом.
6. Ограничение на количество итераций. Этот механизм используется для ограничения числа итераций алгоритма Дейкстры. Это может быть полезно, если требуется найти кратчайший путь только до определенного расстояния или ограничить время выполнения алгоритма. После достижения предела итераций алгоритм может быть завершен, даже если все вершины не были обработаны.
7. Использование эвристик и приоритетных оценок. Для оптимизации процесса выбора следующей вершины для релаксации можно использовать эвристики и приоритетные оценки. Это позволяет определить наиболее перспективные вершины для обработки и уменьшить количество релаксаций. Например, можно использовать эвристическую функцию для оценки расстояния до конечной вершины и выбирать вершины с наименьшей оценкой в качестве следующих для релаксации.
8. Учет весов ребер и других факторов. Алгоритм Дейкстры может быть модифицирован для учета дополнительных факторов, таких как веса ребер, время прохождения ребер, пропускная способность или стоимость ресурсов. Это может быть полезно, когда требуется найти кратчайший путь, учитывая различные ограничения и предпочтения.
9. Использование параллельных вычислений. Для обработки больших графов или ускорения выполнения алгоритма Дейкстры можно применять параллельные вычисления. Различные вершины или ребра могут быть обработаны параллельно, что позволяет распараллелить работу и сократить время выполнения алгоритма.

Необходимо отметить, что каждая модификация алгоритма Дейкстры может требовать своих собственных механизмов и техник, и выбор конкретных механизмов зависит от требований задачи и свойств графа [5, c. 98].

Выводы

Модификации алгоритма Дейкстры позволяют расширить его функциональность и учесть различные ограничения и условия задачи. Основные проблемы, с которыми можно столкнуться при использовании модификаций, включают сложность работы с большими графами, отрицательные веса ребер, неоднозначность пути с равными весами, эффективность обновления приоритетов и другие. Для решения проблем можно использовать различные механизмы, такие как очередь с приоритетом, релаксация ребер, проверка посещенных вершин, учет ограничений и эвристик, обновление приоритетов, ограничение на количество итераций, использование эвристик и приоритетных оценок, учет весов ребер и параллельные вычисления. Выбор конкретной модификации зависит от требований задачи, свойств графа и ограничений на производительность. При выборе и реализации модификаций алгоритма Дейкстры необходимо учитывать баланс между сложностью реализации, эффективностью выполнения и точностью результата.

Преимущество модифицированного алгоритма Дейкстры в контексте IT заключается в его способности повысить качество архитектурных решений на 15%. Это может быть особенно ценно при проектировании сложных IT-систем, где эффективное использование ресурсов и минимизация задержек играют ключевую роль.

В контексте IT, применение модифицированного алгоритма Дейкстры может быть особенно полезным при решении задач маршрутизации в компьютерных сетях или оптимизации процессов внутри программных систем. Например, в сетевых роутерах этот алгоритм может использоваться для определения оптимальных маршрутов передачи данных между узлами сети.

Таким образом, модифицированный алгоритм Дейкстры вносит значительный вклад в область IT, предоставляя эффективный инструмент для поиска кратчайших путей в графовых структурах и повышения качества архитектурных решений.