Базовая ставка дисконта и оптимизация финансовой политики в условиях неопределенности

Инвестиционный проект – это процесс реализации инновационной идеи и ее экономическое обоснование, в результате которого принимается решение о целесообразности воплощения в жизнь.

Не секрет, что существуют разные условия, в которых функционирует тот или иной инвестор. И именно от этих условий зависит ставка дисконтирования, которую он будет использовать при реализации предложенного ему инвестиционного проекта. Рассмотрим некоторые ситуации:

1. Не существует безрисковых направлений вложений денежных средств;
2. Привлекаемый объем кредита не ограничивается по детерминированной ставке p-1, которая не обязательно будет совпадать с депозитной ставкой;
3. На начальном этапе инвестор располагает некоторым капиталом K;
4. Перед инвестором открыто множество Ω всех возможных состояний рынка на шаге 1;
5. Инвестор располагает значениями брутто-доходности ξi(ω) каждого i-го ФТ на шаге 1, которые отвечают каждому состоянию рынка ω Є Ω.

Рассматривая данные ситуации будем считать, что инвестор параллельно не ведет операционной деятельности и не участвует в других инвестиционных проектах. Данная модель, конечно, нереалистична, но она позволяет выявить ряд особенностей оценки эффективности проектов в условиях неопределенности.

Допустим, что на шаге 0 инвестор берет кредит D и вкладывает сумму К + D в некоторый пакет ФТ, имеющий структуру х и зависящую от состояния рынка ω доходность 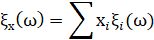, где  – доля i-х ФТ. Тогда на шаге 1 наращенный капитал инвестора составит V(ω) = (K + D)*ξx(ω) – Dρ. Оптимальному пакету отвечает наибольшая ожидаемая полезность: U = M{u[V(ω)]}, где u(V) - функция полезности инвестора, зависящая от его наращенного капитала V, а символ М здесь и далее означает усреднение соответствующего выражения по мере Р. В дальнейшем указание на зависимость доходностей от состояния рынка со будем опускать.

Таким образом, оптимальный пакет будет решением задачи:

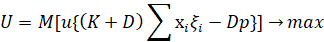  (1)

При ограничениях

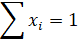;  (2)

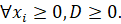 (3)

Для разных инвесторов, отличающихся функциями полезности и или, тем более, набором доступных для них ФТ, оптимальные пакеты будут, вообще говоря, различаться.

Вначале рассмотрим нереальный случай нейтрального к риску инвестора: u(V) = V. Здесь целевая функция будет зависеть только от средних доходностей ФТ:

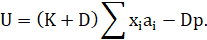 (4)

Поэтому решение оказывается тривиальным: все средства инвестор должен вложить в ФТ с наибольшей средней доходностью. Если ставка кредита больше средней нетто-доходности этого ФТ, кредит не должен привлекаться, если она больше, то кредит следует взять в бесконечно большом (практически - как можно большем) объеме. Если же ставка кредита равна средней нетто-доходности «лучшего» ФТ, то привлечение кредита не изменяет целевую функцию. Реальные инвесторы обычно осторожны. Однако из изложенного вытекает, что если на финансовом рынке есть участники с почти линейной функцией полезности (т.е. почти нейтральные к риску), то либо кредитные ставки должны быть достаточно высоки, либо кредиты должны лимитироваться, чтобы ограничить спрос инвесторов на "дешевые" кредиты.

Для осторожных инвесторов функция u(V) строго выпукла вверх. Тогда хi и D будут максимизировать: 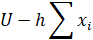 при ограничениях 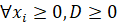, где h - двойственная оценка ограничения 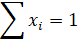. При этом будут выполняться следующие соотношения:

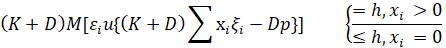(5)

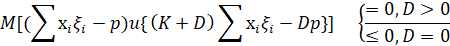(6)

Далее, если мы обозначим 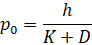 из (5), тогда получим упрощенное выражение:

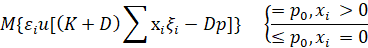(7)

Умножая (7) на  и складывая значения по всем i, найдем уравнение, которое отражает ценность денег для инвестора на шаге 0:

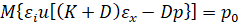(8)

Вычитая из 6 из 8 получим:

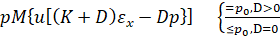  (9)

Как мы видим, равенство ставки кредита и депозита и квадратичной функции полезности приводит к условиям дополняющей нежесткости, которые имеют место в бета-модели. Стоит заметить, что в данной модели не обязательно должна выполняться теорема разделения, то есть оптимальный портфель не должен быть составлен из безрисковых вложений и рыночного портфеля, а также акций с большей или меньшей доходностью, требуемой CAPM. При заданном уровне цен некоторых ФТ инвесторам с одной функцией полезности выгодно купить их, включив в свой оптимальный портфель, а другим инвесторам – выгодно их продать.

Для того чтобы из полученной модели получить ставку дисконта, нужно обратить к величине 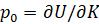, отражающая ценность денег для инвестора на шаге 0. При этом ценность денег на шаге 1 будет рассчитываться по формуле:

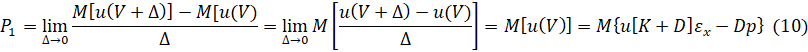
Благодаря формуле 10 можно определить темп падения ценности денег во времени:

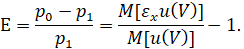 (11)

Значение ставки Е зависит как от параметров рыночной конъюнктуры, так и от функции полезности инвестора, а также от его начального капитала. В силу того, что на рынке может возникнуть ситуация отсутствия безрисковых ФТ, эту ставку называют базовой ставкой дисконта.

Проведя анализ финансовой политики в условиях неопределенности, можно сделать вывод, что разные инвесторы по-разному оценивают возможные изменения на финансовом рынке в будущем, разные методы принятия решений и разные ставки дисконтирования. Финансовое положение инвестора ухудшится только тогда, когда ухудшится конъюнктура финансового рынка. Поэтому успешность деятельности инвестора в длительной перспективе зависит только от его степени возможности, а не от того, согласованы ли его методы и оценки с методами и оценками других инвесторов.