Система поддержки экипажа при экстренной ситуации летательного аппарата

Введение

Ежедневно по всему миру самолеты совершают 120 тысяч полетов и перевозят примерно 12 млн пассажиров. Сегодня число авиапассажиров составляет 4 млрд человек в год, т.е. большая часть населения земли. Ежедневно в мире совершается около 85,000 гражданских авиарейсов, причем речь идет только о гражданской авиации.

Но, согласно статистике [1], в 2018 году в общей сложности случилось 157 несчастных случаев с самолетами и в них погибли 534 человека. Всего за 2019 год в мире произошло 86 авиапроисшествий, восемь из которых закончились летальными исходами, а число жертв авиакатастроф составило 257 человек. В отчетах экспертов констатируется, что наряду с отказами техники одной из частых причин авиакатастроф является попадание самолета в так называемые критические режимы полета.

Так, 29 октября 2018 года произошла одна из наиболее крупных авиационных катастроф. Авиалайнер Boeing 737 MAX выполнял очередной рейс. Остатки самолёта были найдены в море. Все пассажиры и члены экипажа погибли. Позже компания «Boeing» сообщила, что произошел отказ в системе предупреждения сваливания.

Таким образом, можно сделать вывод, что за многолетнюю историю развития авиации проблема обеспечения безопасности летательных аппаратов до сих пор является актуальной.

При проектировании приложений, предназначенных для содействия пилотам, в последнее время активно используются различные способы машинного обучения, что значительно улучшило процент ожидаемых результатов решаемых задач при сравнении со стандартными алгоритмами.

Целью данной работы является описание программного комплекса, предназначенного для следующих задач:

• Классификации критических ситуаций летательного аппарата на основе автоматического анализа данных телеметрии.
• Предупреждение летчика о нештатной ситуации.
• Предоставление пилоту рекомендуемых значений для успешной посадки летательного аппарата.

1. Критические ситуации

Во время проведения полёта может возникнуть ситуация, при которой летчику потребуется полная мобилизация сил, для предотвращения катастрофы. Такие опасные формы, в которые может попасть летательный аппарат, обычно называют критическими ситуациями. По большей части, данные режимы, происходят по причине ошибки пилотирования, отказа одной из систем. Поэтому оценка границ области таких критических ситуаций и разработка способов разрешений нештатных ситуаций являются неотъемлемой частью при моделировании нового летательного аппарата.

Для действующих воздушных судов свойственны следующие типичные критические формы движения [2]: сваливание, штопор, срыв, кренение.

Для критических форм движения самолёта присуще сильное влияние нелинейности аэродинамических характеристик, кинематических связей и т.д. Из-за этих нелинейных эффектов развитие критических форм движения зависит от исходных условий полёта, начальных значений параметров движения и т.п.

2. Отказы

Нормативный уровень надёжности самолёта закладывается при проектировании. Для удобства проектирования и анализа, самолёт разделяется на следующие основные функциональные группы (системы): планер, силовая установка, гидро- и пневмосистемы, взлётно-посадочные устройства, система управления, пилотажно-навигационное оборудование, система электроснабжения, радиоэлектронное оборудование, система кондиционирования и жизнеобеспечения, погрузочно-разгрузочное, пассажирское и специальное оборудование [3].

Приведённое разделение, впрочем, как и любое другое, не строгое, но общепринятое.

3. Недостатки современных методов защиты летательных аппаратов от критических режимов пилотирования

Обеспечение безопасности летательного аппарата одной из наиболее первостепенных задач. Данный вопрос стал более актуален по причине непрерывного роста перелетов в год. Рациональный выбор типа самолёта, его свойств и органов управления создают определенные возможности для улучшения качества безопасности [4].

На рисунке 1 представлена схема центральных величин, проверяемых вычислительной системой. Именно благодаря данным параметрам существует вероятность предупреждения пилота и возможной критической ситуации

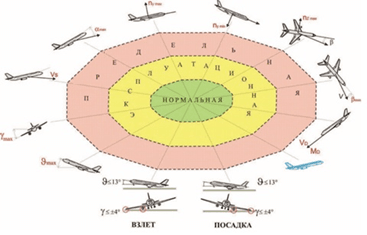
Рис. 1. Схема ключевых параметров летательного аппарата

Применение современного оборудования позволяют значительно снизить количество авиационных крушений, особенно, за счёт снижения человеческого фактора, который, зачастую, оказывает существенное влияние при нештатной ситуации.

Но к большому сожалению, современные методы защиты летательных аппаратов имеют ряд недостатков:

• Большое количество обрабатываемой информации.
• Отсутствие обрабатывания параметров как единой системы [5].

Важно отметить, что второй недостаток напрямую связан с первым. Так, во время полёта, вычислительные системы ежесекундно получают и обрабатывают свыше 700 параметров [6]. Для обработки такого большого объема данных необходима новейшая аппаратура, которой могут похвастаться только самолёты военной и большой авиации. В остальных же случаях, бортовой компьютер не рассматривает данные как единую систему, а проверяет параметры по-отдельности на предмет их приближения к критическому значению.

Решением этих параметров может стать вычислительная система, способная обрабатывать данные параллельно, а не один за одним, как это происходит сейчас. За счет этого, значительно снизится время обработки данных, и, как следствие, появится возможность рассматривать входящую информацию как единую систему.

4. Анализ вычислительной системы с аппаратом дискретной математики

В МГТУ им. Н.Э. Баумана разработана вычислительная система с многими потоками команд и одним потоком данных, в которой на аппаратном уровне реализован аппарат дискретной математики. Данная компьютерная система позволит сократить время обработки информации, поступающей на бортовой компьютер, и рассматривать полученные данные как единую систему. Процессор «Leonhard» новая универсальная вычислительная система. Она позволила сократить время обработки больших объемов данных за счет аппаратного ускорения действий над множествами и структурами данных. Процессор реализует набор команд высокого уровня над множествами и структурами данных. Новая архитектура позволяет более эффективно решать задачи дискретной оптимизации, основанные на моделях множеств, графов, и отношений.

Данная система основана на следующих принципах:

Принцип 1. Для возможности параллельной обработки структур данных в состав вычислительной системы вносится аппаратное устройство (Процессор обработки структур), который обрабатывает лишь ту часть информации, которая определяет взаимные отношения хранимых данных, т.е. структурную часть структур данных. Универсальный Центральный процессор обрабатывает информационную составляющую структур данных [7].

Рис. 2. Вычислительная система с аппаратной поддержкой операций над множествами и структурами данных

Принцип 2. В вычислительной системе с аппаратной поддержкой операций над структурами данных один поток данных обрабатывается несколькими потоками команд. Для обработки каждого потока команд используется отдельное устройство: Центральный процессор применяется для обработки данных потоком команд из локальной оперативной памяти; Процессор обработки структур также связан с локальной памятью команд, а также памятью для хранения структур (рисунок 3).

Рис. 3. Взаимодействие устройств в вычислительной системе с аппаратной поддержкой операций над множествами и структурами данных

5. Алгоритм «К Ближайших Соседей»

Иcходя из способностей микропроцессора «Leonhard» метод машинного обучения «К Ближайших Соседей», в основе которого лежит [8] построение графов и поиск кратчайшего расстояния до соседней вершины подходит лучше, чем другие методы машинного обучения.

Подробно, алгоритм работы «К Ближайших соседей» описан в [9], сейчас же будут описаны только основные аспекты.

Первым этапом необходимо обучить систему с помощью авиасимулятора на предмет распознавания той или иной критической ситуации.

При поступлении нового «предмета изучения» сначала необходимо рассчитать евклидово расстояние, путем суммирования квадрата расстояния между точками по формуле (1):

,  (1)

В случае точного определения критической ситуации работа алгоритма закончена, если же не все результаты одного класса, то необходимо воспользоваться взвешенным голосованием. Известно, чем больше евклидово расстояние, тем менее значимый вклад вносит голос. Голоса за класс находятся по формуле (2):

,  (2)

где 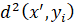  – квадрат расстояния от известной записи Yi, до новой X’, n – количество известных записей класса, для которого рассчитываются голоса.

Полученные значения сравниваются, и выбирается то, которое является наибольшим.

Данный метод считается одним из наиболее точных в машинном обучении. Его ключевым недостатком являлась потребность в использовании больших вычислительных ресурсов. Однако, благодаря применению системы на основе микропроцессора «Leonhard» с набором команд дискретной математики [7], данный недостаток нивелируется.

6. Выбор наилучшей альтернативы

В случае приближения критической ситуации или отказа одной из систем – время, затраченное экипажем на принятие дальнейших действий может играть решающую роль. Требуется выбрать и выдать пилоту наиболее предпочтительный вариант развития событий по глобальному критерию.

Для простоты визуализации будут рассматриваться только 3 параметра (скорость летательного аппарата, дальность до цели, отказ топливной системы) и 3 возможных альтернативных сценариев продолжения полета, проведенных заранее. Важно отметить, что данные примеры взяты исключительно для простоты понимания читателем и не несут под собой физического смысла.

Вектор представлен ниже:

F(x)={f₁(x), f₂(x), f₃(x)}.

Каждый из параметров является лингвистическая переменна, область которых определяется термами):

"Скорость летательного аппарата (км/ч) " = {"Минимальная" (0..38), "низкая" (39..80), "Средняя" (81..120), "Высокая" (119..160), "Оптимальная" (>161)};

"Расстояние до посадки (км)" = {"Очень далеко" (>3300), "Далеко" (2200..3300), "Приемлемо" (1799..2200), "Близко" (799..1798), "Очень близко" (0..798)};

"Отказ топливной системы" = {" Слив топлива на Земле ", " Заправка заданного количества топлива ", " Перекачка топлива в предрасходные и расходные баки, междубачковая перекачка", " Хранение топлива ", "Подача топлива в двигатель" };

Опыт использования метода анализа иерархий показывает результаты высокого качества при применении девятибалльной шкалы предпочтений по Саати [10]:

{9, 8, 7, 6, 5, 4, 3, 2, 1, 1/2, 1/3, 1/4, 1/5, 1/6, 1/7, 1/8, 1/9}.

Целочисленные значения этой шкалы имеют следующую значимость:

1 – одинаковая;

3 – низкая;

5 – высокая;

7 – очень высокая;

9 – полная доминация;

2, 4, 6, 8 – равные с нечётными значениями.

В таблице 1 представлены значения отношений термов на примере критерия «Высота». Остальные сравнения происходят аналогично.

Таблица 1

Значения отношений термов на примере критерия «Высота»

Высота	Минимальная	Низкая	Средняя	Высокая	Оптимальная
Минимальная	1	1/3	1/5	1/7	1/9
Низкая	3	1	1/2	1/3	1/4
Средняя	5	2	1	1/2	1/3
Высокая	7	3	2	1	1/2
Оптимальная	9	4	3	2	1

В качестве возможных альтернативных сценариев также рассмотрим 3 случая: A={A₁,A₂,A₃}, где – A₁ сценарий полета №1; A₂ – сценарий полета №2; A₃ – сценарий полета №3.

В таблице 2 указан анализ сравнения альтернативных сценариев полёта летательного аппарата по параметрам.

Таблица 2

Анализ сравнения альтернативных сценариев полёта летательного аппарата по параметрам

Частные критерии	Альтернативные варианты продолжения действий экипажем
	A1	A2	A3
f1(x)	Оптимальная	Средняя	Средняя
f2(x)	Очень близко	Очень далеко	Очень далеко
f3(x)	Перекачка топлива	Перекачка топлива	Подача топлива в двигатель

В качестве входных критериев примем случайные величины и определим их термы, соответствующие их численным значениям:

f₁(x) =89 км\ч;

f₂(x) = 2257 км;

f₃(x) = Слив топлива на Земле.

6.1. Расчет вектора приоритета глобальных параметров

Сначала следует рассчитать матрицу сравнений [A_f nXn], которая показывает отношение параметров относительно их самих. Каждый параметр сопоставляем с нечетным числом по девятибалльной шкале предпочтений Саати. К примеру: Расстояние до посадки = {"Очень далеко" (1), "Далеко" (3), "Приемлемо" (5), "Близко" (7), "Очень близко" (9)}.

Следующим этапом, необходимо расставить коэффициенты превосходства между параметрами. Полученные результаты, приведены в таблице 3.

Таблица 3

Матрица парных сравнений глобальных критериев

	f1(x)	f2(x)	f3(x)
f1(x)	1	1/2	5
f2(x)	2	1	7
f3(x)	1/5	1/7	1

Чтобы определить вектор приоритетов критериев 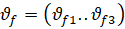 матрицы [A_f nXn], требуется рассчитать величину по формуле 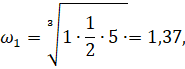(3):

 (3)

Данную операцию надо выполнить для каждой строки матрицы. Элементы вектора ϑ_f  будут определяться по формуле 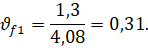(4):

(4)

Например, первая координата  будет вычисляться по формуле (3) и (4):

Остальные элементы вычисляются аналогично. В итоге получаем вектор приоритетов глобальных критериев:

6.2. Расчет векторов приоритета превосходства альтернатив

По принципу расчета определения приоритета глобальных критериев, необходимо получить коэффициенты превосходства альтернатив. Также следует составить матрицу парных сравнений для всех параметров. Для составления матрицы, сопоставляются альтернативы к определённому параметру. Чем меньше разница между входным параметром и эталонными значениями из таблицы 2, тем сильнее приоритет. Матрица имеет размерность 3х3. Затем будет необходимо рассчитать вектор приоритетов, по той же схеме, что и ϑ_f.

В таблицах 4-6 представлены матрицы сопоставления альтернатив по каждому параметру. Также для каждой матрицы определен ситуационный вектор.

Таблица 4

Матрица сопоставления альтернатив по параметру «Расстояние до посадки»

Дальность до цели	A1	A2	A3
A1	1	1	1
A2	1	1	1
A3	1	1	1

Результирующий вектор: .

Таблица 5

Матрица сопоставления альтернатив по параметру «Скорость летательного аппарата»

Видимость	A1	A2	A3
A1	1	1	1
A2	1	1	1
A3	1	1	1

Результирующий вектор: .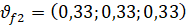

Таблица 6

Матрица сопоставления альтернатив по параметру «Отказ топливной системы»

Высота	A1	A2	A3
A1	1	1	3
A2	1	1	3
A3	1/3	1/3	1

Результирующий вектор: .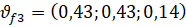

6.3. Формирование итоговых значений каждой из альтернатив

Следующим этапом предстоит рассчитать набор предпочтительных весовых коэффициентов. Данное значение рассчитывается по формуле (6):

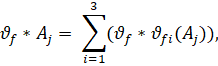   (5)

где j=1..3.

Итоговые результаты глобального приоритета показаны в таблице 7.

Таблица 7

Итоговые результаты глобального приоритета

Альтернативы	Веса частных критериев			Вес ϑf*Aj
	ϑf1	ϑf2	ϑf3	0,41+0,011
A1	0,33	0,33	0,43	0,34
A2	0,33	0,33	0,43	0,64
A3	0,33	0,33	0,14	0,04
ϑf	0,31	0,59	0,08

С помощью полученных результатов можно увидеть, что наиболее благоприятной альтернативой, при данных начальных параметров, является «второй сценарий».

7. Алгоритм работы программы

Исходя из всего вышесказанного можно составить схему работы нового метода защиты летательного аппарата от попадания в критические ситуации. Ее можно разделить на следующие этапы:

• Отправление авиа-симулятором данных для обучения системы.
• Обучение системы.
• Внедрение в бортовую систему самолёта.
• Предупреждение пилота о возможной критической ситуации.
• Вывод наиболее благоприятного сценария о продолжении полёта.

Функциональная схема итогового программного продукта представлена на рисунке 4.

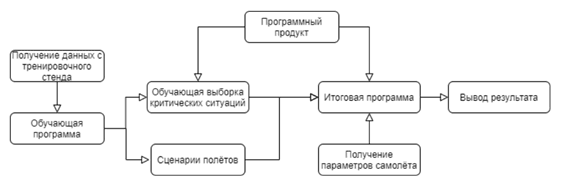
Рис. 4. Функциональная схема программного продукта

Заключение

В работе выполнен анализ различных отказов летательного аппарата, кратко рассмотрены критические ситуаций самолета и недостатки современных способов защиты.

В качестве решения был предложен метод, основанный на алгоритмах машинного обучения и аппаратной платформы дискретной математики. Выполнен анализ данной платформы. В качестве метода машинного обучения был выбран алгоритм «К Ближайших Соседей». Также был предложен метод выбора наилучшей альтернативы продолжения полёта в случае возникновения нештатной ситуации.

В результате получена функциональная схема итогового программного продукта.