Необходимость усовершенствования уравнений Максвелла с целью описания корпускулярно-волнового дуализма

Необходимость усовершенствования обычных уравнений Максвелла назрела давно, так как в том виде записи, в котором они были представлены, они не только не могли сами описать наипростейшие объекты мироздания, но и не могли обеспечить связь корпускулярных и волновых свойств в объектах мироздания. Более того, переход от уравнений Максвелла к электромагнитным волновым уравнениям был также сделан с парадоксами и ошибками. При этом такие объекты мироздания как электронные и мюонные нейтрино, которые двигались со скоростью света, вообще не поддавались описанию с помощью обычных уравнений Максвелла, хотя при такой скорости движения они обязаны были быть представлены через электромагнитные компоненты. Поэтому в данной статье мы покажем, как путём исключения парадоксов получаются усовершенствованные уравнения Максвелла, на основе которых обеспечивается формирование корпускулярно-волновых свойств и определяется отношение массы протона к массе электрона.

Надо отметить, что требование необходимости усовершенствования уравнений Максвелла уже практически было введено в обычные уравнения Максвелла, например, через сторонние токи и через комплексную электрическую и магнитную проницаемость. Надо было только признать очевидное, это наличие проекций электрических и магнитных составляющих на время. Вначале покажем вывод усовершенствованных уравнений Максвелла на основе наличия комплексной магнитной проницаемости.

Берём известное обычное уравнение Максвелла в частных производных в виде:

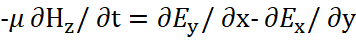           (1)

При представлении в электродинамике значения магнитной проницаемости в комплексном виде, что, кстати, позволяет решить проблему изменения направления движения по принципу Гюйгенса-Френеля в силу взаимодействия со средой распространения, имеем:

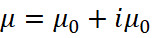        (2)

Здесь i=(-1)^1/2. При подстановке получаем:

         (3)

То есть классическая электродинамика при допущении наличия комплексных значений электрической и магнитной проницаемости потребовало и комплексный вид для уравнений Максвелла. Здесь значение μ₀ одинаковой величины в действительной и мнимой части, так как среда не изменяет объект, движущийся со скоростью света. В противном случае объект распадается или будет расти до бесконечности, в силу отсутствия закона сохранения количества. Иными словами, среда характеризует взаимодействие без изменений при сохранении движущегося объекта. То есть, мы при условии закона сохранения количества имеем:

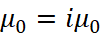    (4)

Здесь мнимая единица i выступает как атрибут противоположности и фактически выражает закон, по которому на действие одной противоположности происходит противодействие, что и выражается возвратом со знаком минус при возведении в квадрат. Некоторые читатели могут подумать, что приравнивание действительной части к мнимой части – это наша выдумка. Однако в квантовой механике давно известно равенство iФ=А₄=A_t, при А₁=A_х, А₂=A_у, А₃=A_z [1]. Собственно приравнивание А₄ к проекции на время A_t также было сделано в электродинамике Фейнманом [2]. Далее не нарушая вида уравнения мы умножаем числитель и знаменатель мнимой производной на скорость света:

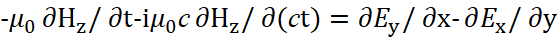    (5)

С математической точки зрения ничего не поменялось, а с физической точки зрения мнимая производная отражает противоположность, где за счёт скорости света длина и время меняются местами. Иначе при сохранении одинакового вида представления объектов нет отличий и это исключает наличие противоположностей. При этом, на основе преобразований Лоренца-Минковского, время однозначно преобразовывается в длину, а длина во время в равных количествах в соответствии с СТО и ОТО Эйнштейна. Соответственно, переход в противоположность от времени к длине связан со скоростью света по формуле [3]:

x⁰=ct.     (6)

В данном случае х⁰ отражает длину координаты, в которую происходит преобразование длины при движении (изменении). Иными словами, среда распространения – это не некий вакуум, а объект, состоящий из противоположностей, выраженных через длину и время в соответствии с СТО и ОТО Эйнштейна. Если бы не было взаимного преобразования длины во время, и наоборот, в соответствии с СТО и ОТО Эйнштейна, то длина и время были бы независимы друг от друга, а это означает, что они были бы замкнуты на себя и друг для друга не существуют, и о противоположностях в одном объекте не было бы речи, но это не наблюдается на практике.

Кроме того, раз мы наблюдаем на практике противоположности в объекте, выраженные через длину и время (другого описания при движении нет), то говорить не о чём без этих величин. С учётом того, что противоположности связаны через скорость света (скорость обмена), то покой и движение в противоположности меняются местами, а это выражается и сменой проекций, где длина переходит во время, а время в длину. Повторяем, иначе не было бы и самих противоположностей, если бы вид сохранялся. Отсюда имеем:

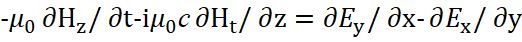    (7)

Понятно, что левая часть уравнения (7) характеризует замкнутый обмен между противоположностями, аналогично тому, как такой же замкнутый обмен характеризует и правая часть уравнения (7). И в данном случае для составляющей Н под мнимой производной не остаётся других проекций как проекции на время, так как в противном случае для Н нет преобразований и в противоположностях сохраняется одинаковый вид, что исключает наличие самих противоположностей и противоречит преобразованиям Лоренца-Минковского по СТО и ОТО Эйнштейна. Таким образом, мы получили вывод необходимости усовершенствования уравнений Максвелла из соблюдения формул классической электродинамики и преобразований Лоренца-Минковского по СТО и ОТО Эйнштейна. Собственно и сам комплексный вид уравнения с мнимой составляющей это не наша выдумка, и это уже было сделано Дираком, а до него Шредингером. Несколько ниже мы покажем, что усовершенствованные уравнения Максвелла представляют собой и простейшие объекты мироздания в виде электронных и мюонных нейтрино и антинейтрино на основе уравнений квантовой механики. Однако, чтобы доказать необходимость усовершенствования уравнений Максвелла надо обеспечить формирование объектов от простого вида к сложному виду, и показать, например, переход от усовершенствованных уравнений Максвелла к электромагнитной волне. С этой целью мы должны вспомнить, что в уравнениях Максвелла при описании принципа Гюйгенса-Френеля в среде распространения электромагнитной волны не смогли обойтись без использования неких сторонних токов j_E, j_H (с исключением при этом неких движущихся реальных зарядов, которые в среде распространения нет) в виде [4]:

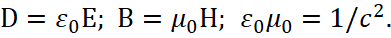    (8)

Значения плотности сторонних токов мы представили с разными знаками аналогично тому, как замкнутые величины rot H и rot Е дают разные знаки производных по времени ∂D/∂t и -∂B/∂t, что обеспечивает замкнутый взаимный переход. Далее пойдём по общепринятому пути и применим к первому уравнению операцию ротора (rot). По сути, это означает воздействие другого объекта, что даёт его изменение за счёт взаимодействия:

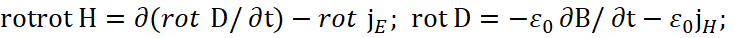
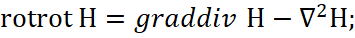                (9)

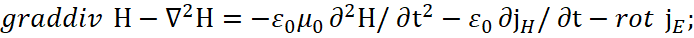
Аналогично применим операцию ротор и ко второму уравнению, что, по сути, означает влияние объектов друг на друга, выраженных через дифференциальные уравнения, а операция ротора соответствует изменениям за счёт воздействия. В итоге имеем:

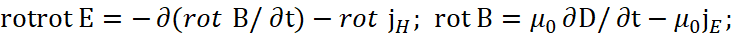
             (10)

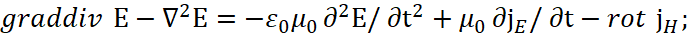
Очевидно, что значения divE и divH не относится к определению значений реальных зарядов, так как их в среде распространения нет. Поэтому вместо обычных зарядов в соответствии с классической электродинамикой [4] для сторонней плотности зарядов имеем:

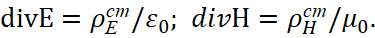    (11)

Но вот тут проблема, связанная с тем, что нет проекций E и Н ни на одну из проекций по длине, так как сторонние заряды не имеют ничего общего с обычной плотностью зарядов на проекции по длине и зафиксировать их на практике нельзя. Отсюда, так как нельзя использовать значения Е и Н на основе проекций на значения по координатам длин, только и остаётся, что считать Е и Н проекциями на время, раз по координатам их зафиксировать нельзя. Соответственно при этом такие проекции Е_t и Н_t должны иметь противодействие друг к другу, что выражается через знак перед значениями сторонней плотности зарядов, кроме того мы учитываем из квантовой механики по преобразованию сторонних токов по Лоренцу формулу j^ст=cρ^ст [5].

Отсюда следует:

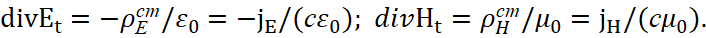 (12)

После подстановки имеем:

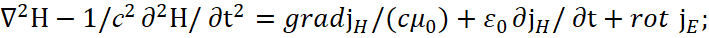
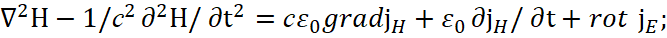     (13)

Понятно, что сторонние токи – это четырёхмерные вектора в пространстве и времени, аналогично тому, как это было предложено Фейнманом для вектор потенциалов.

В левых частях уравнений (13) мы имеем уравнения волны, а в правых частях уравнений сторонние токи. Но, одновременно, по теории классической электродинамики [6] вектор потенциалы имеют вид:

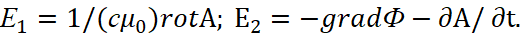    (14)

При этом по классической электродинамике также известно, что вектор потенциалы имеют однозначную связь в нашей системе наблюдения при описании движения заряженной частицы [7]:

     (15)

Но, в варианте наличия только среды распространения, заряженных частиц нет. Отсюда единственный вариант, при котором v=c, а A=Ф/с. Соответственно, используя аналогичный принцип суперпозиции плотности сторонних электрических токов [8], который используется в классической электродинамике, можно определить значение вектора Е=Е₁+Е₂ в виде:

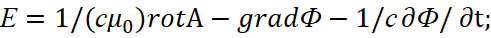    (16)

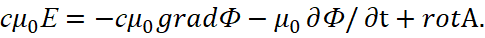
Отсюда имеем два уравнения для сравнения:

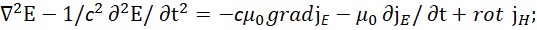
    (17)

Мы видим, что если считать что Ф=j_E, а А=j_H, то мы при совпадении правых частей уравнений фактически получаем уравнение Гельмгольца [9] для левых частей уравнений вида:

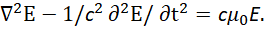    (18)

При нормировке на величину Е с переходом на нормированную функцию W получим:

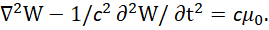    (19)

Далее мы считаем, что константы электрической и магнитной проницаемости среды отражают динамику движения объектов в противоположности. В этом случае наличие изменений в нашей системе наблюдения, не может происходить без изменений в противоположности, тоже в виде движения, которая связана с нашей системой через скорость света. В противном случае противоположности не имели бы взаимного обмена с сохранением количества и в этом случае отсутствовали бы корпускулярно-волновые объекты. Так как противоположности связаны через скорость света, то эквивалент представления движения в противоположности можно выразить в виде величины:

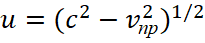    (20)

Здесь v_пр – отражает интегральное усреднённое значение скорости в противоположности от всех объектов связанное с кинетической энергией. Далее с учётом того, что ε₀μ₀=1/c² мы можем выразить значения констант электрической и магнитной проницаемости с отражением движения в противоположности в виде:

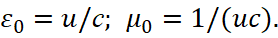    (21)

С учётом такого представления констант электрической и магнитной проницаемости, а также при m₀=1/c [10], мы можем выразить уравнение (19) в виде:

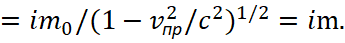    (22)

Здесь, мы введением в правой части мнимой единицы i учитываем то, что имеется связь электромагнитной волны со скоростью движения по СТО и ОТО не в нашей системе наблюдения, а в противоположной системе. Иными словами, электромагнитное излучение это результат движения объектов в противоположности, что соответствует идее Луи де Бройля. Повторим, что здесь мы считаем, что m₀=1/c и этот результат соответствует формуле энергии Эйнштейна, что мы показали в [10]. По сути m₀=h, где h – постоянная Планка (именно эта величина отражает минимально возможный объект в мироздании), что характеризует общую взаимосвязь глобальных противоположностей по нашей теории через формулу сh=1 [11]. Подчеркнём, что данная формула соответствует количественным преобразованиям в мироздании, и мироздание ничего не знает о системе измерения СИ и СГС, которые привели к парадоксу чёрных дыр связанному с радиусом Шварцшильда. Таким образом, мы видим, что волновые процессы в одной противоположности связаны с массой в другой противоположности. То есть шумовое электромагнитное излучение определяется не спонтанным появлением и исчезновением неких виртуальных фотонов из вакуума, а определяется пространственно-временным искривлением на основе СТО и ОТО Эйнштейна. Действительно, чтобы иметь решение уравнения (22), мы должны иметь функцию W вида:

     (23)

Понятно, что мы имеем не соответствие с функцией Луи де Бройля для отдельной частицы, хотя имеем зависимость от массы, получаемой от движения в противоположности, что связано с тем, что функция W отражает процесс двойного дифференцирования и электромагнитного волнового движения со скоростью света уже в нашей системе наблюдения. В то же время волновая функция Луи де Бройля связана с движением частицы со скоростью меньшей, чем скорость света и она фактически характеризуется функциями в системе уравнений Дирака. Этот парадокс будет нами разрешён при описании корпускулярно-волновых объектов через уравнение энергии Эйнштейна и связан он с тем, что электромагнитная волна представляет собой взаимодействие противоположных объектов. Собственно необходимую зависимость от массы с учётом функции Луи де Бройля можно было бы получить на основе вектор потенциалов в последнем уравнении (17) при однократном дифференцировании. Однако указанный вид через вектор потенциалы не соответствует виду дифференциальных уравнений в системе Дирака, и поэтому необходимо показать, каким образом можно перейти от представления через вектор потенциалы к дифференциальным уравнениям в системе Дирака, через которые отражается движение частицы как корпускулярно-волнового объекта со скоростью меньшей, чем скорость света. Выше мы показали, как из классической электродинамики на основании комплексной электрической и магнитной проницаемости получаются усовершенствованные уравнения Максвелла вида (7). Если представить указанную запись в векторном виде, то мы при замене в (8) сторонних токов на проекции электромагнитных составляющих на время получим:

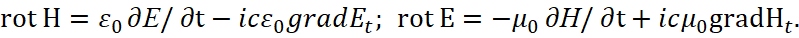     (27)

И повторим ещё раз, что появление мнимой составляющей связано с выполнением принципа Гюйгенса-Френеля по огибанию волной препятствия на основании комплексных значений электрической и магнитной проницаемости. Аналогичный вид можно получить и на основе вектор потенциалов при равенстве Е₁=Е₂ в системе уравнений (14), так как иное означало бы что изменения в противоположностях которые представлены через А и Ф не равны, что противоречит закону сохранения количества. Отсюда мы можем записать:

 (28)

Так как в варианте наличия только среды распространения, заряженных частиц нет, то на основе уравнения (15) возможен единственный вариант, при котором v=c, а A=Ф/с. Если учесть, что значение Ф в grad Ф при росписи в частных производных также будет выражаться через проекцию на время (иных проекций просто не остаётся), то в результате имеем уравнение:

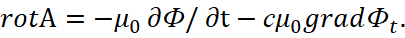     (29)

В этом случае изменения в одной противоположности равны изменениям в другой противоположности. Физически, изменение электромагнитных составляющих в нашей системе наблюдения выражается законом Фарадея и описывается обычными уравнениями Максвелла. Понятно, что в силу закона сохранения количества (иначе одна из противоположностей исчезает) мы имеем симметрию физических законов в противоположностях, что и дало вид (29) для вектор потенциалов. Однако симметрия физических законов в противоположностях также означает, что для выполнения физического закона огибания волной препятствия мы в противоположности также должны иметь комплексные значения констант электрической и магнитной проницаемости (иное исключает совпадение законов физики), что, кстати, означает представление этих констант как корпускулярно-волновых объектов. При этом переход в противоположность, как это было показано на основе комплексной проницаемости в (7) должен выражаться за счёт умножения члена grad Ф_t на мнимую единицу. Мы видим, что уравнение (29) при умножении на –i величины grad Ф_t будет полностью соответствовать второму уравнению в (27) в виде:

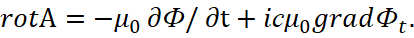     (30)

И это соответствует симметрии физических законов в противоположностях. Как было показано выше, взаимодействие усовершенствованных уравнений Максвелла, с представлением производных от проекций на время электромагнитных составляющих в виде сторонних токов, выразилось в воздействии оператора rot на два первых уравнения в системе (8). И это взаимодействие привело к формированию нового объекта в виде электромагнитной волны в соответствии с уравнениями Гельмгольца. Фактически мы имеем реакцию на изменения вектор потенциалов по закону Фарадея в нашей системе наблюдения в виде электромагнитной волны. А так как электромагнитные составляющие являются противоположностью к вектор-потенциалам, то отсюда, как и для проекций на время, противоположное значение мы должны выразить через умножение на мнимую единицу, так как только действительный вид даёт обнуление величин, а это означает чудеса. Отсюда мы должны записать:

    (31)

При этом, меняя знак в члене grad Ф на противоположный знак по отношению к варианту уравнения (30), мы вычитание меняем на сложение, что соответствует условию, по которому сложение в одной противоположности означает вычитание в другой противоположности. Иное бы означало, что при переходе в противоположную систему наблюдения у нас нет изменений в физических процессах, а это отрицает и наличие самих противоположностей и исключает формирование новых объектов при изменениях.

Так как физические процессы в противоположностях реализуются одинаково, то аналогичная форма записи должна быть и для электромагнитных составляющих в виде:

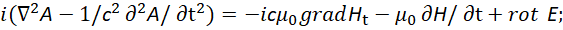
    (32)

Здесь А – функция, которая отражает волновые процессы в противоположности с выполнением уравнения Гельмгольца. Фактически это вектор-потенциал, так как в противоположности ничего другого и быть не может в волновом виде, что, кстати, показано и в классической электродинамике. И это происходит в результате взаимодействия на основе двух усовершенствованных уравнений Максвелла, которое выразилось в изменениях через применение к уравнениям операции ротора (rot). По сути, на основании (31) и (32) мы видим, что изменения по закону Фарадея в одной противоположности формируют излучаемый корпускулярно-волновой объект в другой противоположности.

Так как воздействие может быть применено к чему-то реально существующему, то соответственно возникает вопрос, а что в реальности представляют усовершенствованные уравнения Максвелла как объекты?

Чтобы ответить на этот вопрос надо вспомнить систему уравнений Дирака, которая получается из уравнения энергии Эйнштейна для описания движения частицы.

Взятое изначально Дираком уравнение энергии Эйнштейна имеет вид количественной зависимости кинетической и потенциальной энергии друг от друга в статике. Чтобы перейти к динамике изменений через количественные превращения надо представить уравнение энергии Эйнштейна через функциональные зависимости между объектами мироздания. С этой целью Дирак в качестве функций, характеризующих объекты мироздания, использовал волновые функции Луи де Бройля - Ψ, а количественные превращения в виде изменений обозначил через воздействие операторов на эти функции. При этом он получил систему уравнений из этих объектов мироздания, которые при взаимодействии через подстановку одних уравнений в другие должны были давать исходное уравнение энергии Эйнштейна, что обеспечивало устойчивость полученной частицы-объекта с соблюдением закона сохранения количества. В этом случае он провёл так называемую «линеаризацию» уравнения энергии Эйнштейна в виде [12]:

E = c (P² + m₀²c²)^1/2 = c (Σα_k∙P_k),           (33)

здесь k изменяется от 0 до 3; P₀=M₀c; P₁=P_x; P₂=P_y; P₃=P_z.

При этом мы имеем:

E² = c² (P² + m₀²c²)= c² ∙ 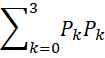     (34)

Чтобы установить, каким условиям должны удовлетворять величины α_k, с учётом разложения уравнения энергии Эйнштейна на систему начальных уравнений в динамике через функции, возведём обе части соотношения (33) в квадрат.

E² = c² (P² + m₀²c²)= c²  =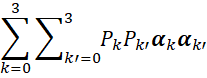

= c²/2 .     (35)

Чтобы соблюсти соответствие данной формы исходному уравнению энергии Эйнштейна Дирак использовал матрицы для разложения:

α1 =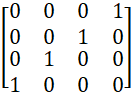, α2 =,    (36)

α3 =, α4 =ρ3=.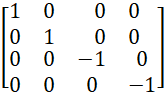

Далее он вместо реальных значений энергии и импульсов ввёл операторы Е и р в виде:

E=iћ , p=-iћ,     (37)

Соответственно эти операторы он применил к неким вероятностным волновым функциям Ψ в системе уравнений:

(Е-m₀c²)Ψ₁-c(P_x-iP_y)Ψ₄-cP_zΨ₃=0,

(Е-m₀c²)Ψ₂-c(P_x+iP_y)Ψ₃+cP_zΨ₄=0,    (38)

(Е+m₀c²)Ψ₃-c(P_x-iP_y)Ψ₂-cP_zΨ₁=0,

 (Е+m₀c²)Ψ₄-c(P_x+iP_y)Ψ₁+cP_zΨ₂=0.

В дифференциальном представлении указанная система будет выглядеть:

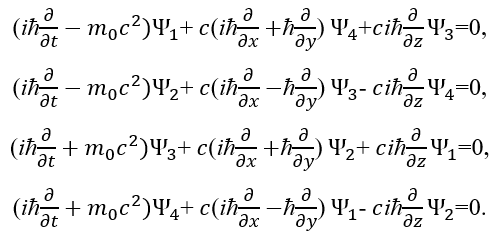    (39)

В соответствии с классикой квантовой механики эта система уравнений Дирака при массе покоя равном нулю m₀=0 превращается в волновые уравнения нейтрино и антинейтрино (рис.).

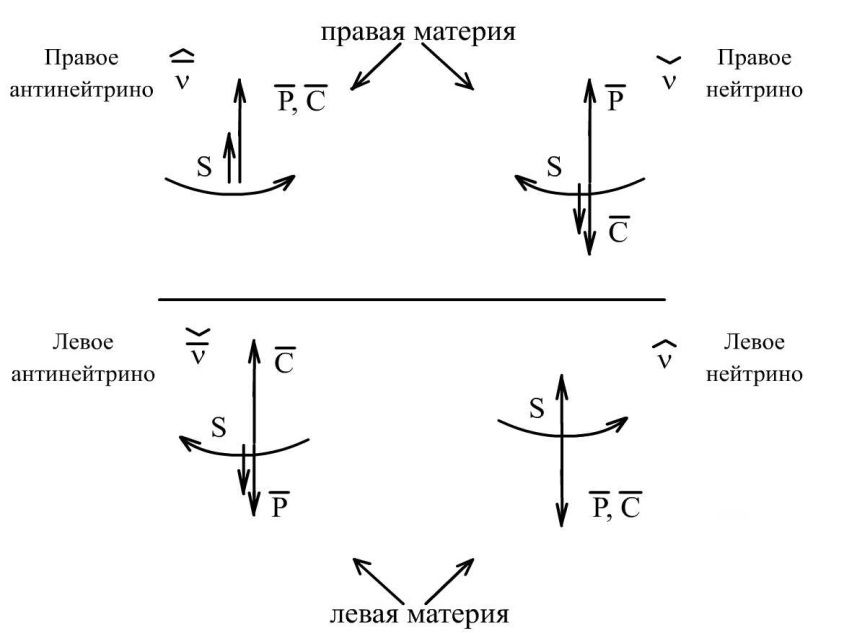
Рис. Нейтрино и антинейтрино

Понятно, что понятие материи не имеет в теории никакого физического обоснования, так как не имеет математического описания с наличием количества, и оно связано с непониманием учёными происходящих в мироздании процессов. Для описания нейтрино и антинейтрино используется уравнение с двухрядными матрицами Паули (уравнение Вейеля), либо уравнение Дирака, расщепляющееся на два независимых уравнения [13].

     (40)

Мы видим, что отличия между первой и второй парой в системе (40) только в обозначении функций. При этом мы не можем оставить прежние обозначения функций, отражающих составные объекты, так как нейтрино и антинейтрино отражают объекты, двигающиеся со скоростью света, что конечно подразумевает иное взаимодействие составных объектов, которое было для частицы изначально, иначе бы не было изменений. Так как распространение нейтрино и антинейтрино происходит со скоростью света, то понятно, что в этом случае волновые функции могут быть только электромагнитными функциями. Отсюда сравним на соответствие второго и четвёртого уравнения системы (40) с видом усовершенствованных уравнений Максвелла:

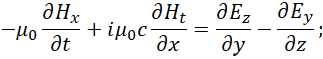
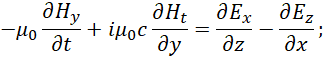
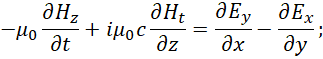    (41)

 

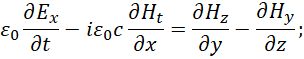
То есть мы можем представить второе и четвёртое уравнение в системе (40) аналогично уравнениям (41) в виде:

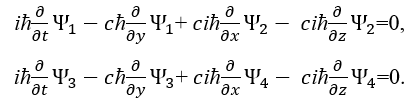    (42)

Сократив на постоянную Планка ћ, и умножив на –i получим:

=0,

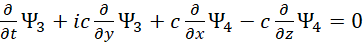.     (43)

Иными словами, мы имеем два идентичных уравнения, которые могут только отличаться через функции. Однако, если исходить из усовершенствованных уравнений Максвелла, то мы можем их выразить как:

,    (44)

.

Иными словами мы получаем физические аналоги реализаций функций Ψ₁ и Ψ₂, а также Ψ₃ и Ψ₄, выраженных через реальные электромагнитные составляющие по (41) с учётом констант электрической и магнитной проницаемости, то есть состояния среды. Это означает, что усовершенствованные уравнения Максвелла отражают реальные объекты в виде электронных и мюонных нейтрино и антинейтрино. Собственно это объясняет эффект аннигиляции электрона и позитрона, которые описываются системой уравнения Дирака с получением фотонов. Понятно, что данный эффект превращения может быть связан только с взаимодействием электронных и мюонных нейтрино и антинейтрино, так ничего иного и нет. Кроме того, мы имеем физический смысл различий между электронными нейтрино (антинейтрино) и мюонными нейтрино (антинейтрино) за счёт констант электрической и магнитной проницаемости без выдумывания левой и правой материи по рисунку. Первое и третье уравнение в системе (40) отличается от второго и четвёртого уравнения в этой системе знаком сложения вместо знака вычитания, который обозначал ротор (rot) в виде:

,

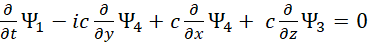.    (45)

Это связано с тем, что в системе уравнений Дирака (40), уравнения не могут иметь идентичный вид, так как в этом случае происходит ассоциативное сложение без взаимодействия. Разница в знаках между уравнениями, можно характеризовать как результат участия в формировании массы покоя нейтрино и антинейтрино, которые мы видим при распаде частиц, а наличие обратно-пропорциональной связи между функциями как противоположностей, показанная в квантовой механике [14] характеризует различие в виде электронных и мюонных нейтрино (антинейтрино). Это различие связано с движением объектов в противоположности и также есть на практике при распаде частиц. Понятно, что этот набор электронных и мюонных нейтрино и антинейтрино обеспечивает замкнутое взаимодействие в системе уравнений Дирака с соблюдением закона сохранения количества в соответствии с формулой уравнения энергии Эйнштейна и отражает движущуюся частицу (корпускулярно-волновой объект).

Таким образом, через усовершенствованные уравнения Максвелла на основе (8), где проекции на время электромагнитных составляющих заменены плотностью сторонних токов, с учётом взаимодействия через операцию rot получается представление электромагнитной волны с подчинением уравнениям Гельмгольца через функции вектор потенциалов (иное исключало бы связь противоположностей) для магнитной напряжённости поля волны в виде:

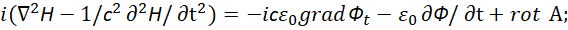
     (46)

И для электрической напряжённости поля волны в виде:

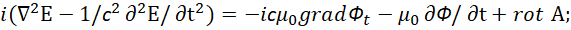
    (47)

С учётом симметрии физических законов в противоположностях мы должны записать вид для волны от вектор потенциала Ф как:

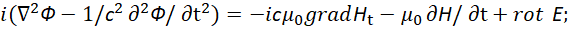
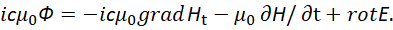    (48)

И для вида волны от вектор потенциала А как:

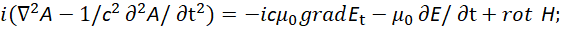
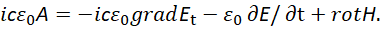    (49)

Мы знаем, что уравнения Дирака выводятся из уравнения энергии Эйнштейна. При этом связь функций Дирака с электромагнитными составляющими нами установлена, так как при массе покоя равном нулю мы получаем, что функции усовершенствованных уравнений Максвелла соответствуют функциям уравнений Дирака. Отсюда естественно предположить, что использование электромагнитных функций в системе уравнений Дирака также должно приводить к соответствию уравнению энергии Эйнштейна, тем более, что объекты, при взаимодействии с другими объектами, описываются электрическими и магнитными составляющими. При умножении на мнимую единицу i уравнений из системы Дирака (39) получаем вид:

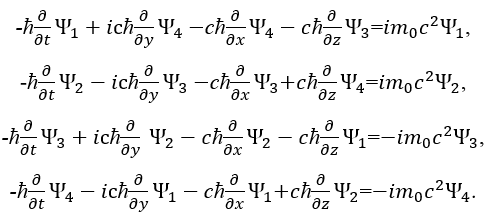    (50)

Аналогично мы можем выписать нижние уравнения в частных производных из (48) и (49) с представлением совпадения по знакам:

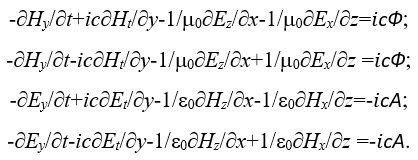    (51)

При этом, первое и третье уравнение по знакам не совпадают с уравнениями два и четыре, что говорит об ином порядке взаимодействия составляющих, так как в противном случае было бы ассоциативное сложение или вычитание.
Ясно, что при сравнении системы уравнений Дирака (50) и системы (51) на основе электромагнитных функций необходимо показать идентичность функций, так как сам вид уравнений совпадает. Следует отметить, что волновые функции Луи де Бройля в системе уравнений Дирака и электромагнитные функции в (51) совпадут лишь в том случае, если каждое уравнение в (51) рассматривается в системе наблюдения аналогичной той, которая используется Дираком. Иными словами, электромагнитные составляющие, аналогично функциям Луи де Бройля, должны отражаться в системе уравнений Дирака как производные от разных переменных по координатам длины и значению времени. Мы покажем этот переход ниже. Видно, что для того, чтобы привести функции в (51) к единообразному виду, как в (50) надо поменять значения ET на HT, и наоборот. 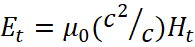Это можно сделать, если учесть разницу на константы электрической и магнитной проницаемостей в среде по координатам длины, исходя из равенства  и , то есть ‒ это связь, которая должна быть в противоположности между подвижным и неподвижным объектом по СТО с учётом отсчёта от системы координат, перемещающейся со скоростью света. Действительно, в соответствии с формулой (21), имеем 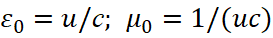, и в этом случае Ht=uEt, и Et=1/uHt, где u определяется по формуле (20), и связывается с интегральной усреднённой скоростью, характеризующей кинетическую энергию объектов в противоположности. Так как у нас симметричные преобразования по формулам (46-49), то для вектор потенциалов при проекции их на время, мы будем иметь аналогичные преобразования, так как меняется только система наблюдения, а законы физики остаются те же. Отсюда верны уравнения:

    (52)

Если учесть, что 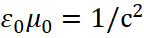, то получим следующий вид уравнений:

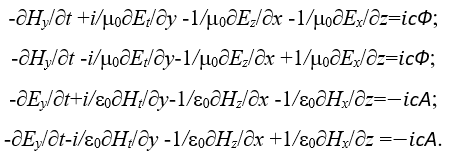    (53)

Мы видим, что первые два уравнения в системе (53) отличаются по электромагнитным функциям от последних двух, а для представления в виде системы уравнений Дирака с подчинением уравнению энергии Эйнштейна их надо привести в одинаковый вид. С этой целью константы электрической и магнитной проницаемости в соответствии с формулой (21) представим в виде некоторой общей переменной u и тогда система уравнений (53) примет вид:

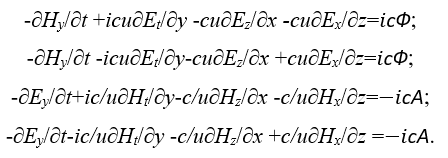    (54)

Учитывая связь между электрическими и магнитными составляющими в виде Н=сЕ (это изначальная связь между противоположностями через скорость света без учёта СТО, так как нет зарядов в пространстве) мы можем записать:

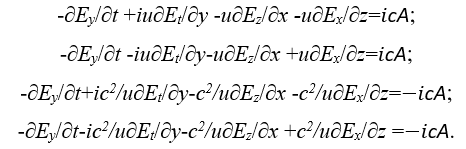    (55)

При этом в (55) считаем, что вектор потенциалы также связаны через скорость света (свойство симметрии при наблюдении из противоположности относительно той системы, где Н=сЕ), так как мы ещё не имеем представления корпускулярного объекта при дифференцировании электромагнитных функций через значение скорости в нашей системе наблюдения:

Ф=сА.     (56)

Учитывая, что в системе уравнениях Дирака коэффициент при волновой функции Ψ без наличия производной отражает энергию массы покоя m₀ =1/c, то мы имеем связь в виде m₀c² Ψ =cΨ. Соответственно это условие будет выполняться, если А=Е. То есть, в данном случае мы выбрали вариант системы наблюдения, когда вектор потенциал А отражается через Е. В итоге имеем:

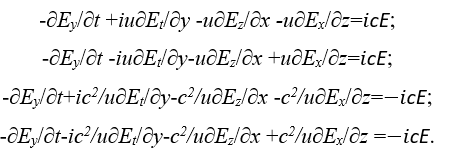    (57)

В этом случае, по аналогии с системой уравнений Дирака, мы получаем, что при начальных функциях E, E_x ,E_y, E_z, E_t мы должны удовлетворить четырём уравнениям для соответствия уравнению энергии Эйнштейна. Однако, это возможно только в том случае, если в каждом из уравнений (системы наблюдения) значения функций (объектов) E_x, E_y, E_z, E_t выступают в качестве значений изменяемых переменных, относящихся к разным системам представления систем координат, и отражают разные функции вида Ψ₁ и Ψ₂, а также Ψ₃ и Ψ₄, как это принято в системе уравнений Дирака. В этом случае значения функций – объектов E_x, E_y, E_z, E_t имеют представление по всем четырём координатам, то есть полностью определяются в пространстве и времени и не имеют независимости от пространства и времени.

В итоге имеем разложение по координатам, где волновые функции имеют вид:

Ψ₁=Е₁={E_x1, E_y1, E_z1, E_t1}, Ψ₂=Е₂={E_x2, E_y2, E_z2, E_t2},

Ψ₃=Е₃={E_x3, E_y3, E_z3, E_t3}, Ψ₄=Е₄={E_x4, E_y4, E_z4, E_t4}.        (58)

В этих функциях напряжённость электрического поля с проекцией на время Е_t в результате приведения к единообразному виду стала играть роль функций E_y1, E_y2, E_y3, E_y4. Это означает, что представление объекта и компонент зависит от системы наблюдения, что и определяет наличие противоположностей. Собственно это условие уже практически было установлено, когда в зависимости от системы наблюдения определяется представление электрических и магнитных компонент, а СТО и ОТО Эйнштейна утвердило преобразование длины во время и наоборот. А это и означает, что в зависимости от системы наблюдения одна и та же компонента отражает разное представление. Фактически мы имеем замкнутое взаимодействие четырех объектов (аналогично замкнутому взаимодействию по координатам длины и величине времени в инвариантной форме) с отражением этих объектов в пространственно-временной среде. Представим эти функции аналогично волновым функциям Шрёдингера [15], но без нормировочного коэффициента в виде постоянной Планка:

Ψ(t,r)=exp[-i(E_tt-P_xx-P_yy-E_zz)]=exp[-i(Еt-Рr)].    (59)

В этом случае уравнения (57) распишем по функциям в соответствии с системой Дирака в виде:

-∂Ψ₁/∂t-icΨ₁ +iu∂Ψ₄/∂y -u∂ Ψ₄/∂x -u∂Ψ₃/∂z=0;

-∂Ψ₂/∂t -icΨ₂-iu∂Ψ₃/∂y-u∂Ψ₃/∂x +u∂ Ψ₄/∂z=0;     (60)

-∂Ψ₃/∂t+icΨ₃+ic²/u∂ Ψ₂/∂y-c²/u∂ Ψ₂/∂x -c²/u∂Ψ₁/∂z=0;

-∂Ψ₄/∂t+icΨ₄-ic²/u∂Ψ₁/∂y-c²/u∂Ψ₁/∂x +c²/u∂ Ψ₂/∂z =0.

C учётом операции дифференцирования по Ψ имеем:

i(Е-c)Ψ₁-iuP_xΨ₄-uP_yΨ₄-iuP_zΨ₃=0,

i(Е -c)Ψ₂-iuP_xΨ₃+uP_yΨ₃+iuP_zΨ₄=0,    (61)

i(Е+с)Ψ₃-iс²/uP_xΨ₂-с²/uP_yΨ₂-iс²/uP_zΨ₁=0,

i(Е+с)Ψ₄-iс²/uP_xΨ₁+с²/uP_yΨ₁+iс²/uP_zΨ₂=0.

Далее умножаем уравнения на –i:

(Е-c)Ψ₁-uP_xΨ₄+iuP_yΨ₄-uP_zΨ₃=0,

(Е -c)Ψ₂-uP_xΨ₃-iuP_yΨ₃+uP_zΨ₄=0,    (62)

(Е+с)Ψ₃-с²/uP_xΨ₂+iс²/uP_yΨ₂-с²/uP_zΨ₁=0,

(Е+с)Ψ₄-с²/uP_xΨ₁-iс²/uP_yΨ₁+с²/uP_zΨ₂=0.

С учётом выражения одних функций через другие для свободной частицы без внешнего электромагнитного поля получаем:

Ψ₁=(uP_xΨ₄-iuP_yΨ₄+uP_zΨ₃)/(Е-c),

Ψ₂=(uP_xΨ₃+iuP_yΨ₃-uP_zΨ₄)/(Е-c),    (63)

Ψ₃=(с²/uP_xΨ₂-iс²/uP_yΨ₂+с²/uP_zΨ₁)/(Е+с),

Ψ₄=(с²/uP_x Ψ₁+iс²/uP_yΨ₁-с²/uP_zΨ₂)/(Е+с).

Далее подставляем одни функции вместо других, что собственно и характеризует взаимодействие, и сокращаем подобные члены:

Ψ₁=c²[P_x(P_xΨ₁+iP_yΨ₁-P_zΨ₂)-iP_y(P_xΨ₁+iP_yΨ₁-P_zΨ₂)+

+P_z(P_xΨ₂-iP_yΨ₂+P_zΨ₁)]/[(Е-c)(Е+с)],     (64)

Ψ₁=c²[P_x²Ψ₁+iP_xP_yΨ₁- P_xP_zΨ₂-iP_yP_xΨ₁+P_y²Ψ₁+iP_yP_zΨ₂+

+P_zP_xΨ₂-iP_zP_yΨ₂+P_z²Ψ₁]/[(Е-c)(Е+с)].

При m₀=1/c, получаем уравнение корпускулярно-волновых объектов соответствующего возведению формулы энергии Эйнштейна в квадрате:

(Е²-m₀²c⁴)Ψ₁=c²(P_x²Ψ₁ +P_y²Ψ₁+P_z²Ψ₁).    (65)

При взятии квадратного корня из обеих частей уравнения (65) получаем уравнение энергии для отдельных частиц в виде:

ЕΨ₁^1/2=±[m₀²c⁴+c²(P_x²+P_y²+P_z²)] ^1/2Ψ₁^1/2.    (66)

При сравнении с (23) мы видим, что функция Ψ₁^1/2 соответствует функции W, и это означает, что корпускулярное движение в виде противоположных частиц (зарядов) в одной противоположности описывает электромагнитное излучение в другой противоположности.

Сокращая на волновую функцию, получаем уравнение энергии Эйнштейна для частицы в чистом корпускулярном виде:

Е=±[m₀c⁴+c²(P_x² +P_y²+P_z²)]^1/2.    (67)

Аналогичный результат мы можем получить и для других волновых функций, которые отображают иные системы наблюдения. Здесь следует отметить, что мы в соответствии с (67) имеем фактически отражение заряда частицы за счёт знака, то есть по (67) характеризуется движение электрона или позитрона. Однако как быть с описанием таких частиц как протон и антипротон, которые также присутствуют при взаимодействиях? Здесь следует вспомнить, что в (57) мы выбрали вариант А=Е, то есть, вариант системы наблюдения от вектор потенциал А. Однако при выборе отражения другой системы наблюдения через вектор потенциал Ф, с учётом (56) мы получаем систему уравнений:

    (68)

Учитывая связь между электрическими и магнитными составляющими в виде Н=сЕ (это изначальная связь между противоположностями через скорость света без учёта СТО) мы можем записать:

    (69)

Понятно, что система наблюдения от вектор потенциала Ф уже не совпадает с системой наблюдения от вектора Е, и эта связь имеет вид: Ф=сЕ/ε₀=с²/uE. Иными словами при замене Е на А мы имеем аналог формулы (15).

В итоге имеем:

    (70)

Далее по аналогии в соответствии с системой Дирака имеем:

-∂Ψ₁/∂t-ic²/uΨ₁ +iu∂Ψ₄/∂y -u∂ Ψ₄/∂x -u∂Ψ₃/∂z=0;

-∂Ψ₂/∂t -ic²/uΨ₂-iu∂Ψ₃/∂y-u∂Ψ₃/∂x +u∂ Ψ₄/∂z=0;    (71)

-∂Ψ₃/∂t+ic²/uΨ₃+ic²/u∂ Ψ₂/∂y-c²/u∂ Ψ₂/∂x -c²/u∂Ψ₁/∂z=0;

-∂Ψ₄/∂t+ic²/uΨ₄-ic²/u∂Ψ₁/∂y-c²/u∂Ψ₁/∂x +c²/u∂ Ψ₂/∂z =0.

C учётом операции дифференцирования по Ψ получаем:

i(Е-c²/u)Ψ₁-iuP_xΨ₄-uP_yΨ₄-iuP_zΨ₃=0,

i(Е -c/u)Ψ₂-iuP_xΨ₃+uP_yΨ₃+iuP_zΨ₄=0,    (72)

i(Е+с²/u)Ψ₃-iс²/uP_xΨ₂-с²/uP_yΨ₂-iс²/uP_zΨ₁=0,

i(Е+с²/u)Ψ₄-iс²/uP_xΨ₁+с²/uP_yΨ₁+iс²/uP_zΨ₂=0.

Далее умножаем уравнения на –i:

(Е-c²/u)Ψ₁-uP_xΨ₄+iuP_yΨ₄-uP_zΨ₃=0,

(Е -c²/u)Ψ₂-uP_xΨ₃-iuP_yΨ₃+uP_zΨ₄=0,

(Е+с²/u)Ψ₃-с²/uP_xΨ₂+iс²/uP_yΨ₂-с²/uP_zΨ₁=0,    (73)

(Е+с²/u)Ψ₄-с²/uP_xΨ₁-iс²/uP_yΨ₁+с²/uP_zΨ₂=0.

С учётом выражения одних функций через другие для свободной частицы без внешнего электромагнитного поля получаем:

Ψ₁=(uP_xΨ₄-iuP_yΨ₄+uP_zΨ₃)/(Е-c²/u),

Ψ₂=(uP_xΨ₃+iuP_yΨ₃-uP_zΨ₄)/(Е-c²/u),    (74)

Ψ₃=(с²/uP_xΨ₂-iс²/uP_yΨ₂+с²/uP_zΨ₁)/(Е+с²/u),

Ψ₄=(с²/uP_x Ψ₁+iс²/uP_yΨ₁-с²/uP_zΨ₂)/(Е+с²/u).

Далее подставляем одни функции вместо других, что собственно и характеризует взаимодействие, и сокращаем подобные члены:

Ψ₁=c²[P_x(P_xΨ₁+iP_yΨ₁-P_zΨ₂)-iP_y(P_xΨ₁+iP_yΨ₁-P_zΨ₂)+

+P_z(P_xΨ₂-iP_yΨ₂+P_zΨ₁)]/[(Е-c²/u)(Е+с²/u)],    (75)

Ψ₁=c²[P_x²Ψ₁+iP_xP_yΨ₁- P_xP_zΨ₂-iP_yP_xΨ₁+P_y²Ψ₁+iP_yP_zΨ₂+

+P_zP_xΨ₂-iP_zP_yΨ₂+P_z²Ψ₁]/[(Е-c²/u)(Е+с²/u)].

В результате получаем уравнение корпускулярно-волновых объектов соответствующего возведению формулы энергии Эйнштейна в квадрате:

(Е²-c⁴/u²)Ψ₁=c²(P_x²Ψ₁ +P_y²Ψ₁+P_z²Ψ₁).    (76)

С учётом формулы (20) имеем:

(Е²-m₀²c⁴/(1-v_пр²/с²)Ψ₁=c²(P_x²Ψ₁ +P_y²Ψ₁+P_z²Ψ₁).     (77)

При переходе к движущимся частицам только в корпускулярном виде имеем:

Е=±[ m₀²c⁴/(1-v_пр²/с²)+c²(P_x² +P_y²+P_z²)]^1/2.    (78)

В этом случае мы приходим к описанию частицы с массой покоя большей, чем масса покоя электрона или позитрона, чего не могла описать классическая квантовая механика.

Ранее по (22) и (23) мы убедились, что частота волновых процессов напрямую связана с константами электрической и магнитной проницаемости. При этом мы показали, что при наличии массы покоя большей, чем масса покоя электрона (позитрона), скорость движения, формирующая такую массу, может относиться только к противоположной системе наблюдения относительно абсолютной системы отсчёта в соответствии с ОТО. И в этом случае потенциальная энергия в одной противоположности выглядит кинетической энергией в другой противоположности. Соответственно возникает вопрос о стабильности частиц с массой покоя выше, чем масса электрона и позитрона и необходимо объяснить, с чем это связано. Для решения этого вопроса надо обратиться к изначальной формуле связи глобальных противоположностей [16] в виде:

cos²(x)+sin²(x)=ch²(w) – sh²(w) =1= const,

exp(ix)exp(-ix)=exp(w)exp(-w) =1.    (79)

Фактически этот закон отражает основную идею представления объектов в противоположностях с условием, что вычитание в одной противоположности представляется сложением в другой противоположности, так как иначе была бы идентичность. Однако по уравнению (79), мы видим, что если в левой части уравнений от знака равенства наблюдается равенство противоположно направленных электромагнитных составляющих, то в правой части, из-за обратно пропорциональной связи противоположностей, будет неравенство, то есть неоднородность, для равенства справа необходимо иметь значение аргумента равное нулю, то есть объект должен отсутствовать. Отсюда вывод - получить одновременно однородность в противоположностях невозможно. Тогда соответственно встаёт вопрос: "При каком неравномерном электромагнитном распределении по частоте и пространственно-временной неоднородности может наступить равновесный замкнутый обмен между глобальными противоположностями?" На основании общей формулы мироздания (79) мы видим, что процесс распада от некоторой начальной величины можно представить в виде: ехр(-g) или 1/ехр(g). В таком виде мы имеем нормированное к единице количество в соответствии с наличием констант. В противоположности распад представиться синтезом с законом сохранения количества: 1-ехр(-g), 1-1/ехр(g). Собственно это эквивалентно принципу радиоактивного распада в [17], а обратный процесс даёт синтез. Соответственно мы имеем распределение аналогичное формуле Планка [18]:

<g>= g·exp(-g)/[1-exp(-g)] = g/[exp(g)-1].     (80)

Данная формула (80) исключает "ультрафиолетовую катастрофу" и соответствует замкнутой системе. То есть, на основании формулы (80) с учётом числа частот, приходящихся на единицу объёма полости, была получена известная формула Планка, откуда вычисляется энергетическое распределение по частотам и определяется максимум спектра излучения ω_мах. Далее мы вспомним, что пространственно-временное искривление в мироздании определяется соотношением констант электрической и магнитной проницаемости по формуле: 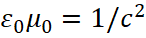. С учётом μ₀=1/(cu), ɛ₀=u/с, где u=(c²-v_пр²)^1/2, а v_пр – значение интегральной усреднённой скорости движения объектов в противоположности (то есть это отображение кинетической энергии), отношение констант магнитной и электрической проницаемости в этом случае даст значение:

(m₀/e₀)^1/2={[1/(uc)]/[u/c]} ^1/2=1/u=

=1/[c(1-v_пр²/c²)^1/2]=120π    (81)

Мы видим здесь расхождение с системой СИ, которая даёт безразмерный коэффициент, а у нас получается значение измерения в единицах скорости. Однако, значение скорости – v_пр относится к противоположности, а сами противоположности связаны через скорость света, как длина и время, поэтому при переходе в противоположную систему наблюдения, мы должны эту связь учесть через умножение величины 1/u на скорость света, и в результате будем иметь безразмерный коэффициент. Кроме того, мироздание ничего не "знает" о системах измерения и оперирует только количеством, а оно безразмерно. Собственно системы измерения, придуманные учёными дали парадокс радиуса Шварцшильда, когда свет не может выйти из гравитационного поля притяжения так называемой «чёрной дыры», то есть нарушается основной принцип термодинамики, где поглощение равно излучению. Отсюда и была придумана телепортация из «чёрной дыры», то есть пошли чудеса.

Поэтому у нас, полученное соотношение является эквивалентом выполнения СТО Эйнштейна и разница определяется в скорость света, то есть в величину взаимодействия противоположностей. Далее, это значение оказалось в полном соответствии с отношением массы протона к массе электрона с учётом перехода от среднего интегрального значения к максимуму спектра излучения в противоположности за счёт коэффициента 4,965, который был вычислен в [19]:

m_пр/m₀=4,965×(m₀/e₀)^1/2=4,965/u₀=

=4,965/[c(1-v_пр²/c²)^1/2]= 4,965×120π=1871,76.     (82)

Здесь m_пр – масса протона, m₀ – масса электрона. Значение, полученное в (82), отличается от значения, вычисленного в физике m_р/m₀=1836, менее, чем на 2%. И это отличие связано с разным пространственно-временным искривлением в мироздании, то есть неоднородностью. Собственно по (82) следует определять и энергетические характеристики корпускулярно-волновых объектов, так как масса имеет однозначную связь с энергией за счёт умножения на с². Понятно, что взаимодействие меняет параметры электрической и магнитной проницаемости в среде, и это изменяет соотношение масс, в противном случае тока в катушке индуктивности после снятия разницы потенциалов на концах проводов не наблюдалось бы. Таким образом, объект изменяет окружающую среду с формированием противодействия на его действие. Когда влияние объекта прекращается, окружающая среда уже влияет на объект, так как среда не может мгновенно изменить свои параметры из-за наличия скорости света. Иными словами, среда имеет обмен с объектом (а он, не может быть без первоначальных простейших объектов, какими являются электронные и мюонные нейтрино и антинейтрино) и это, кстати, определяет помимо поля излучения и наличие квазистатического электромагнитного поля. Именно это взаимодействие объекта и среды и даёт функцию Луи де Бройля определённой частоты. Иными словами мы имеем некую замкнутую резонансную систему взаимодействия через обмен между объектом и средой.

Таким образом, на основе усовершенствованных уравнений Максвелла нам удалось описать связь электромагнитных волновых процессов с образованием корпускулярных свойств с различной массой покоя от простого представления к сложному представлению, и объяснить устойчивость и разницу масс между протоном и электроном. Именно эту проблему не могла решить классическая электродинамика и квантовая механика для объединения корпускулярных и волновых свойств с получением закона взаимного перехода, хотя фактически для этого все необходимые уравнения были уже практически получены. Иными словами наш анализ с учётом наличия общего пространственно-временного и электромагнитного континуума с описанием любого объекта в 4-х мерном представлении (иное даёт независимость объекта) позволил описать формирование объектов от простого представления к сложному на основе корпускулярно-волнового дуализма.