Актуальность исследования
Актуальность исследования обусловлена широким внедрением цифровых двойников в промышленности, энергетике, транспорте и других высокотехнологичных отраслях. Цифровой двойник опирается на сложные, часто высокоразмерные и нелинейные математические модели, прямое использование которых требует значительных вычислительных ресурсов и затрудняет получение результатов в ограниченные временные интервалы.
Работа в режиме мягкого реального времени предполагает, что расчёты выполняются с допустимой, но строго ограниченной задержкой, обеспечивающей устойчивость и эффективность системы. В условиях непрерывного поступления данных от датчиков и необходимости оперативного обновления состояния объекта задача снижения вычислительной сложности моделей становится ключевой. Недостаточная скорость вычислений приводит к запаздыванию прогнозов и управляющих воздействий, что повышает риск технологических сбоев и потерь.
В этой связи особое значение приобретает разработка и применение алгоритмов редукции сложности, позволяющих существенно уменьшить размерность и ресурсоёмкость моделей при сохранении приемлемой точности и устойчивости. Исследование данных алгоритмов является важным условием практической реализуемости и масштабируемости цифровых двойников в реальных киберфизических системах и обладает высокой теоретической и прикладной значимостью.
Цель исследования
Целью данного исследования является анализ алгоритмов редукции сложности математических моделей и вариантов их интеграции в архитектуру цифровых двойников для обеспечения работы в режиме мягкого реального времени при сохранении требуемой точности и устойчивости моделирования.
Материалы и методы исследования
В качестве материалов использованы научные статьи, обзоры и отраслевые отчёты, посвящённые цифровым двойникам, системам реального времени, методам MOR/ROM и их применению в энергетике, машиностроении и ветроэнергетике.
Методический аппарат включает сравнительный анализ требований к моделям в офлайн-режиме и в режиме мягкого реального времени, классификацию алгоритмов редукции сложности, систематизацию практических кейсов с количественной оценкой выигрыша по времени расчёта и эксплуатационным показателям, а также структурно-функциональный анализ архитектур цифровых двойников с разделением на офлайн- и онлайн-этапы.
Результаты исследования
Цифровой двойник представляет собой многослойную архитектуру, включающую физический уровень оборудования, уровень вторичных систем, коммуникационную инфраструктуру и уровень автоматизированных систем управления. Для каждого из слоёв используются собственные типы математических моделей, которые взаимодействуют друг с другом через обмен данными в реальном масштабе времени.
Для наглядной демонстрации структуры цифрового двойника и взаимосвязи его основных уровней представлена типовая архитектура, характерная для предприятий энергетики и промышленной автоматизации (рис. 1). Она отражает разграничение моделей по функциональным уровням и их роль в формировании единого вычислительного контура цифрового двойника.
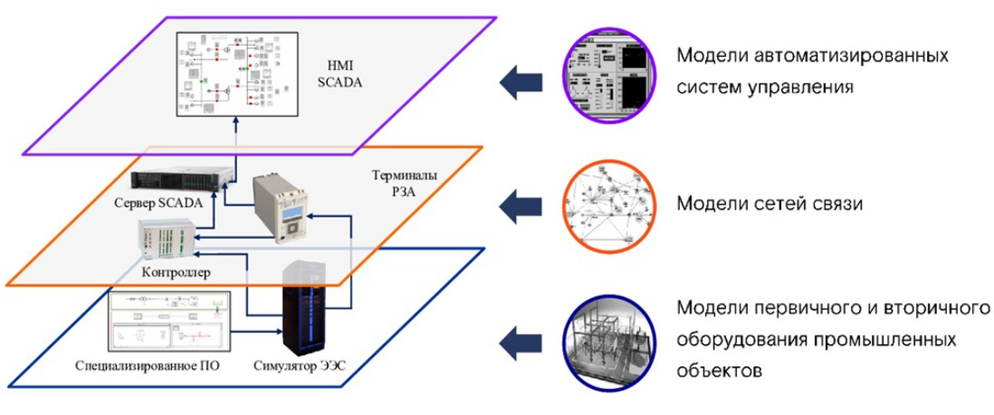
Рис. 1. Архитектура цифрового двойника промышленного объекта [1]
Развитие цифровых двойников тесно связано с динамикой рынка и технологическими трендами. По оценкам аналитических обзоров начала 2020-х годов, мировой рынок технологий цифровых двойников оценивался примерно в 6,9 млрд долларов США в 2022 году и прогнозировался на уровне порядка 73,5 млрд долларов к 2027 году, что соответствует очень высоким темпам роста (более 30% в год) [2].
Стремительный рост объясняется тем, что цифровые двойники внедряются в ключевых сегментах «Индустрии 4.0» – энергетике, машиностроении, транспорте, строительстве, городском хозяйстве – как инструмент повышения эффективности эксплуатации, снижения простоев, оптимизации обслуживания и снижения рисков.
Требования к математическим моделям различаются в зависимости от режима их использования: для традиционного офлайн-моделирования допустимы длительные расчёты и максимальная детализация, тогда как цифровой двойник требует регламентированного по времени пересчёта и устойчивой работы в условиях непрерывного потока данных. Для наглядного сопоставления этих режимов представляется целесообразным свести основные критерии в обобщённую сравнительную таблицу 1, основанную на типичных требованиях, описанных в работах по системам реального времени и прикладным исследованиям цифровых двойников.
Таблица 1
Сравнение требований к моделям при офлайн-моделировании и в режиме мягкого реального времени цифрового двойника
Характеристика | Традиционная численная модель (офлайн) | Модель цифрового двойника (мягкое реальное время) |
Цель вычислений | Проектный анализ, валидация, исследование чувствительности | Непрерывный мониторинг, прогноз и поддержка оперативных решений |
Допустимое время расчёта | Минуты-сутки | Миллисекунды-секунды |
Обновление входных данных | Разово, по сценариям | Непрерывные потоки телеметрии |
Отношение к нарушению дедлайна | Не критично (результат всё равно полезен) | Допустимы редкие нарушения, но задержка ухудшает качество сервиса |
Типичные методы | Полные FEM/CFD-модели, сложные нелинейные постановки | Редуцированные модели, гибрид «полная модель + ROM», ML-аппроксимации |
Вычислительная платформа | Кластеры, суперкомпьютеры, офлайн-серверы | Встраиваемые системы, edge-серверы, облако с жёсткими SLA по задержке |
Алгоритмы редукции сложности (model order reduction, MOR) позволяют заменить исходные крупноразмерные модели динамических систем низкоразмерными приближениями при сохранении ключевых свойств – устойчивости, формы отклика, приемлемой точности. В инженерной практике они используются для ускорения расчётов в задачах управления, оптимизации, многовариантного моделирования и особенно востребованы там, где модель включена в контур цифрового двойника и должна работать в режиме мягкого реального времени.
К классическим проекционным методам относятся сбалансированное усечение, методы Крылова и редуцированный базис (RB). В них строится маломерное подпространство состояний, на которое проецируются матрицы системы; в результате размерность может снижаться с десятков или сотен тысяч до нескольких десятков переменных при контролируемой погрешности. Для задач механики и гидродинамики широко применяется корректное ортогональное разложение (Proper Orthogonal Decomposition, POD), основанное на анализе «снимков» решения полной модели. В нелинейных и параметрических задачах проекция дополняется гиперредукцией (например, методами выборки опорных точек), что снижает стоимость вычисления нелинейных членов.
Наряду с этим интенсивно развиваются данные-ориентированные и гибридные подходы: автоэнкодеры, POD-DL-ROM и другие нейросетевые схемы, в которых динамика описывается в скрытом маломерном пространстве. Такие модели обучаются по результатам высокоточных расчётов и затем используются для очень быстрых прогнозов, что особенно важно при работе цифрового двойника на потоках данных.
Практический эффект MOR хорошо иллюстрирует сравнение времени расчёта полной и редуцированной модели. В инженерных примерах на базе ANSYS показано, что для задач с размерностью порядка десятков тысяч степеней свободы время одиночного стационарного расчёта полной модели сопоставимо с временем построения редуцированной модели порядка 30 уравнений, тогда как последующее многократное использование этой редуцированной модели даёт кратный выигрыш по времени [5].
В таблице 2 представлен пример сокращения времени расчёта при использовании редуцированной модели [4].
Таблица 2
Пример сокращения времени расчёта при использовании редуцированной модели
Размерность системы | Время решения полной модели, с | Время построения ROM (≈30 уравнений), с |
≈ 4 000 | ~0,6 | ~0,9 |
≈ 11 000 | ~2,2 | ~4,0 |
≈ 20 000 | ~15 | ~26 |
Практическое использование алгоритмов редукции сложности математических моделей в цифровых двойниках связано прежде всего с требованием обеспечить прогноз и оптимизацию состояния объекта в режиме мягкого реального времени при ограниченных вычислительных ресурсах. В типичных промышленных сценариях (энергетика, ветроэнергетика, сложное машиностроение) исходные высокоразмерные модели строятся на этапе проектирования и верификации, а затем на их основе создаются редуцированные или суррогатные модели, пригодные для быстрых расчётов в эксплуатационном контуре цифрового двойника.
Для наглядного обобщения типичных эффектов от внедрения алгоритмов редукции в цифровых двойниках различных отраслей можно привести сводную таблицу 3 с данными из опубликованных исследований.
Таблица 3
Примеры эффекта от использования редуцированных моделей в цифровых двойниках
Область применения | Объект/тип цифрового двойника | Выигрыш по вычислительным затратам | Эффект на эксплуатационные показатели |
Тепловая энергетика (УК пароблок) | Цифровой двойник паротурбинной системы 1030 МВт | Использование упрощённых моделей подсистем снижает нагрузку вычислительных ресурсов при онлайн-моделировании (без роста времени отклика) | Рост энергоэффективности блока ~на 0,35% |
Тепловая энергетика (динамика ротора, пуск) | Цифровой двойник ротора паротурбины с онлайн-обновлением | Оптимизация алгоритмов мониторинга уменьшила время расчётов при сохранении точности напряжений | Сокращение времени пуска на ~5,3% (около 32 минут) |
Ветроэнергетика (лопасть ВЭУ) | Структурный цифровой двойник лопасти с ROM | Сокращение времени расчёта отклика ≈ в 400 раз (≈ 7 ч → 1 мин) | Возможность приближённого онлайн-анализа деформаций лопасти |
Ветропарк/энергосистема | Цифровой двойник ветровой электростанции для анализа устойчивости | Уменьшение времени оценки устойчивости на ≈77 % благодаря редуцированным моделям | Увеличение запаса устойчивости примерно на 18% |
Тепловая генерация (контроль и оптимизация) | Гибридный цифровой двойник тепловой электростанции с серией упрощённых моделей подсистем | Сокращение вычислительной нагрузки примерно на 35% при предиктивной аналитике | Снижение времени реакции системы на возмущения и уменьшение простоев до 20–25% |
В архитектурном плане применение алгоритмов редукции подразумевает разделение жизненного цикла модели на тяжёлый офлайн-этап и облегчённый онлайн-этап. На офлайн-этапе, используя высокопроизводительные вычислительные ресурсы, проводится серия детальных расчётов полной модели (например, конечно-элементной модели турбины или лопасти, детального термодинамического цикла станции), выполняется построение снижающего отображения и формируется библиотека редуцированных моделей для различных режимов. На онлайн-этапе цифровой двойник использует выбранную ROM, подстраивая её параметры по потокам данных от датчиков и реализуя прогноз и оптимизацию в пределах допустимой задержки.
Для демонстрации практического применения алгоритмов редукции сложности в составе цифрового двойника целесообразно показать типовой цикл построения и эксплуатации редуцированной модели. На рисунке 2 отражены основные этапы: переход от реального электродвигателя к CAD-модели, дальнейшее формирование полноценной трёхмерной симуляционной модели, применение процедуры MOR для получения ROM-модели и её последующее использование в режиме эксплуатации в виде виртуальных датчиков и soft-sensor технологий. Такая последовательность хорошо иллюстрирует взаимосвязь офлайн-этапа построения цифрового двойника и онлайн-этапа его работы в режиме мягкого реального времени.
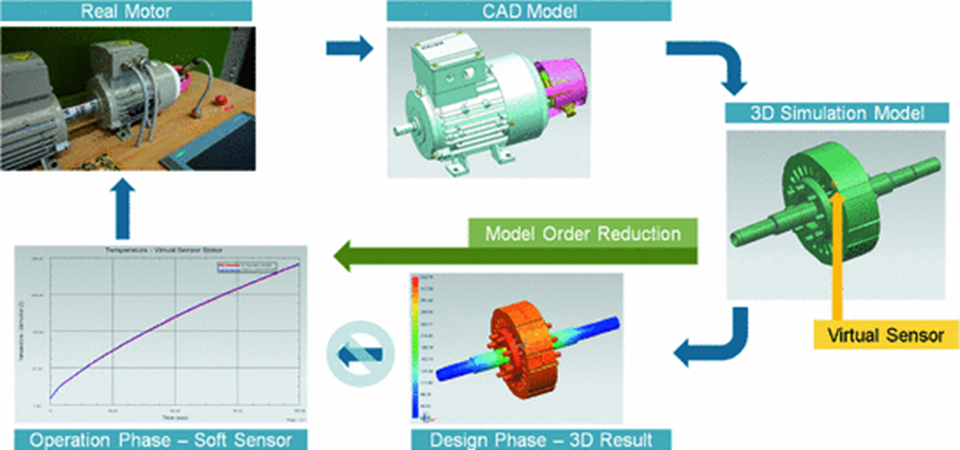
Рис. 2. Цикл разработки и применения редуцированной модели цифрового двойника электродвигателя [3]
Применение алгоритмов редукции сложности неизбежно связано с приближённым характером получаемых моделей. Основной риск состоит в потере точности и адекватности при выходе за диапазон режимов, использованный при построении ROM: при изменении параметров, появлении новых возмущений или переходе к запредельным режимам редуцированная модель может давать существенно искажённые прогнозы.
Дополнительную опасность представляет возможная утрата устойчивости и робастности: модель, корректно работающая в расчётных условиях, при небольшом дрейфе параметров способна становиться чувствительной к шуму и приводить к неверным управляющим воздействиям. Для data-driven и гибридных ROM к этому добавляется зависимость от качества обучающей выборки и риск некорректного поведения вне области данных.
Поэтому при внедрении редуцированных моделей в цифровые двойники необходимо чётко задавать область их применимости, регулярно сверять результаты с полной моделью или измерениями, а также предусматривать процедуры переобучения и актуализации ROM. Без такого контроля использование редукции в безопасностно-критичных системах (энергетика, транспорт, промышленная автоматизация) может приводить к росту технических и эксплуатационных рисков.
Перспективы развития методов редукции связаны с дальнейшим объединением физических моделей и методов машинного обучения. Гибридные модели позволяют сочетать интерпретируемость и устойчивость классических ROM с гибкостью нейросетевых аппроксимаций. Нейросетевые редукторы, включая автоэнкодеры и глубокие ROM-архитектуры, способны автоматически выделять оптимальные маломерные представления сложных процессов и обеспечивать почти мгновенный прогноз. Важным направлением становится онлайновая адаптация, при которой параметры редуцированной модели корректируются по текущим данным, что повышает точность и устойчивость цифрового двойника в меняющихся условиях эксплуатации.
Выводы
Таким образом, без применения алгоритмов редукции сложности реализация цифровых двойников в режиме мягкого реального времени для сложных инженерных объектов практически невозможна из-за высокой вычислительной нагрузки традиционных моделей. Использование проекционных, POD- и гибридных ROM-подходов позволяет многократно сократить время расчёта при приемлемой погрешности и обеспечивает переход от проектных симуляций к эксплуатационному мониторингу, прогнозу и оптимизации. В то же время редуцированные модели требуют строгого задания области применимости, регулярной валидации и механизмов актуализации параметров по текущим данным. Наиболее перспективным направлением развития являются гибридные физико-информационные модели с нейросетевыми редукторами и средствами онлайновой адаптации, способные повысить точность и надёжность цифровых двойников в условиях изменяющихся режимов эксплуатации.

.png&w=640&q=75)