Для повышения эффективности стрельбы из автоматического оружия в патентах [1, 2] предложена схема полусвободного запирания канала ствола, представляющая собой рычажный механизм с ползунами, движущимися в противоположных направлениях.
В процессе проектирования этого механизма возникает необходимость оценки прочности его деталей. С целью определения величин реакций в парах методами теоретической механики [3] составлена математическая модель динамики механизма, расчетная схема которого приведена на рис. 1.
На рис. 1 используются следующие обозначения: P – сила давления пороховых газов, Nk (k=1, …,7) – нормальные реакции связей (реакция N3 представлена проекциями на координатные оси), f – коэффициент трения, r – радиус рычага, h – расстояние от оси рычага 2 до линии действия выступа толкателя 1, φ – угол поворота рычага 2. Предполагается, что центр масс рычага 2 находится на оси его вращения, трением во вращательной паре пренебрегаем.
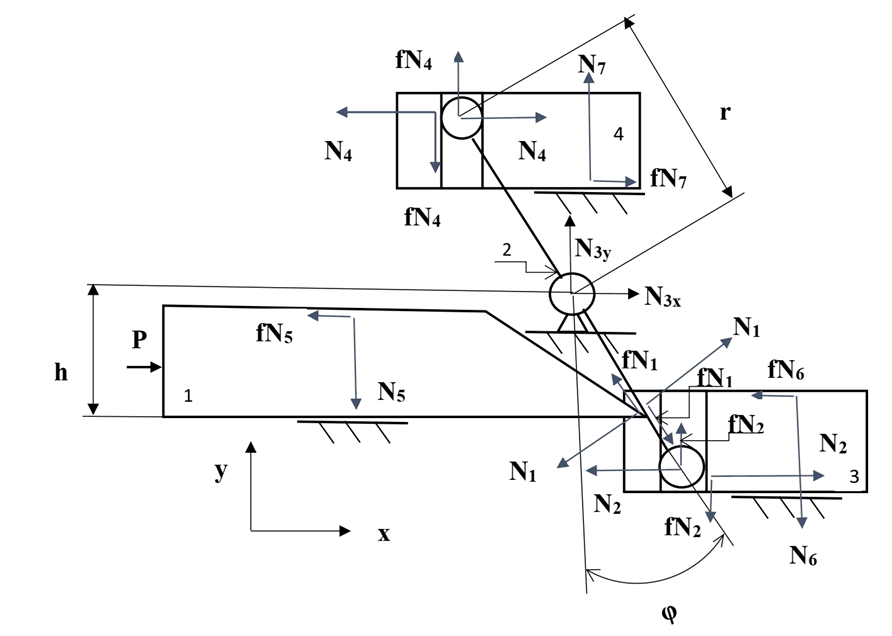
Рис. 1. Расчетная схема рычажного механизма с ползунами, движущимися в противоположных направлениях
Система уравнений, описывающая динамику механизма запирания, имеет следующий вид:
;
;
;
;
;
;
;
;
;
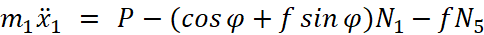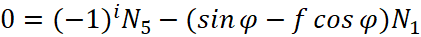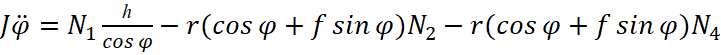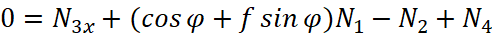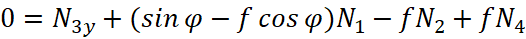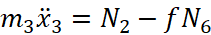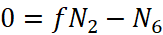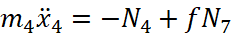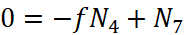где
;
;
;
;
;
, 
, 
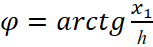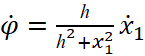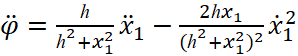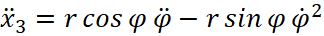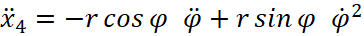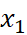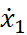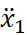– координата, скорость и ускорение затвора соответственно;
, 
, 
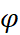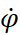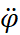– угол поворота, угловые скорость и ускорение рычага соответственно;
m1, m3, m4, J – массы и момент инерции соответствующих звеньев;
i – вариантный индекс [4-6], позволяющий обеспечить условие не отрицательности реакции N5.
Предлагаемое математическое описание было реализовано в виде программы в среде пакета MatLab. Работоспособность программы проверялась на примере моделирования механизма с гипотетическими конструктивными параметрами. Интегрирование проводилось на интервале времени 0 ≤ t ≤ 3.124·10- 3 с, соответствующем наиболее интенсивной нагрузке на механизм. Максимальная величина силы давления порохового газа составила P = 4,728*104 Н.
Расчет проводился при следующих исходных данных.
|
Масса толкателя 1, кг |
2,39. |
|
Массы разбегающихся ползунов m3 = m4. кг |
1,34. |
|
Момент инерции рычага 2 J, кг·м2 |
2,62·10-5. |
|
Радиус рычага r, м |
20·10-3. |
|
Расстояние от оси рычага 2 до линии действия выступа толкателя 1 h м |
10·10-3. |
|
Коэффициент трения f |
0,15. |
|
Вариантный индекс i |
1 |
Интегрирование системы дифференциальных уравнений модели проводилось методом Рунге-Кутта. Полученные при моделировании основные характеристики движения механизма приведены на рис. 2-8.
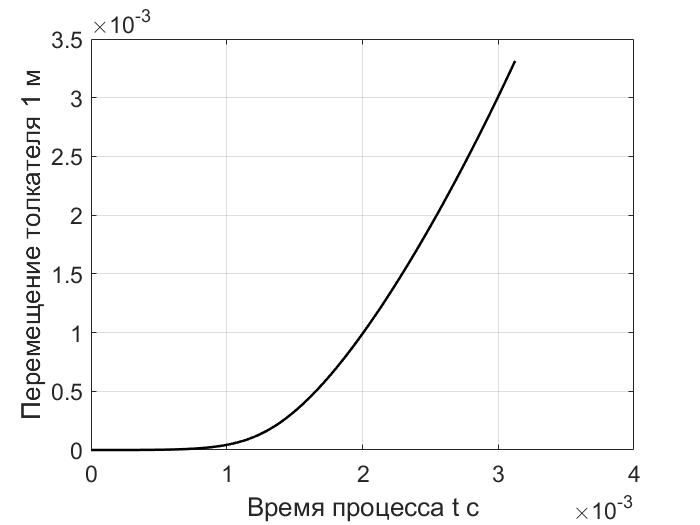
Рис. 2. Зависимость перемещения толкателя 1 от времени
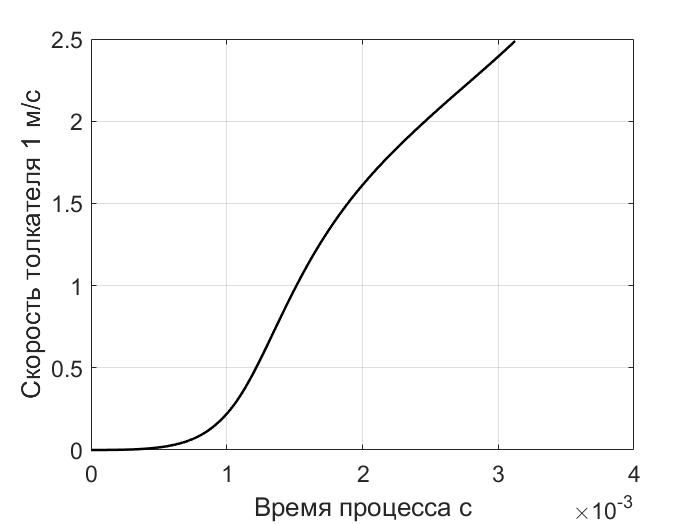
Рис. 3. Зависимость скорости толкателя 1 от времени
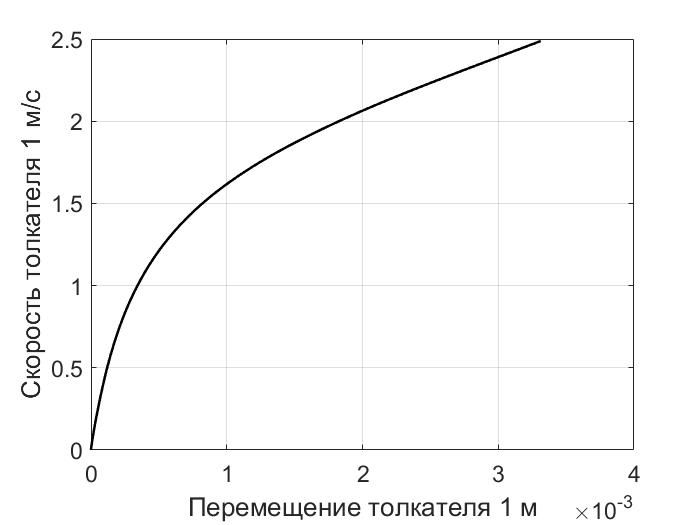
Рис. 3. Зависимость скорости толкателя 1 от его перемещения
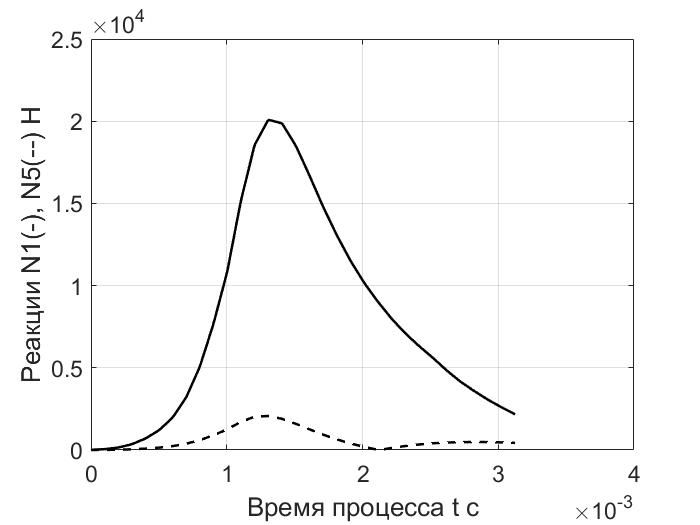
Рис. 4. Зависимость реакций N1, N5 от времени
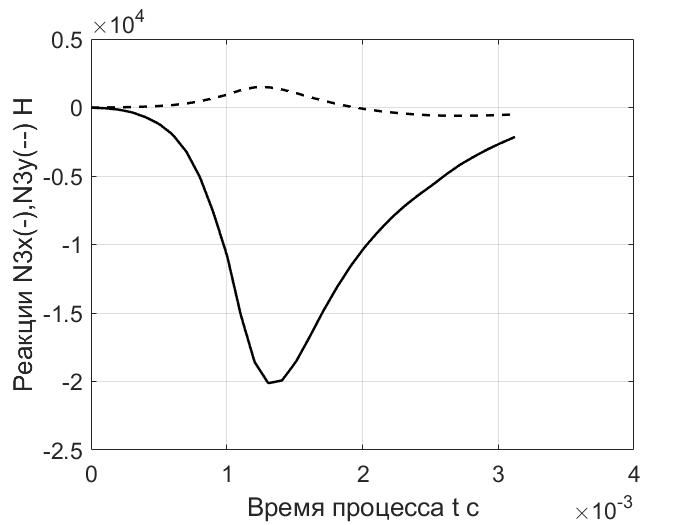
Рис. 5. Зависимость реакций в шарнире от времени
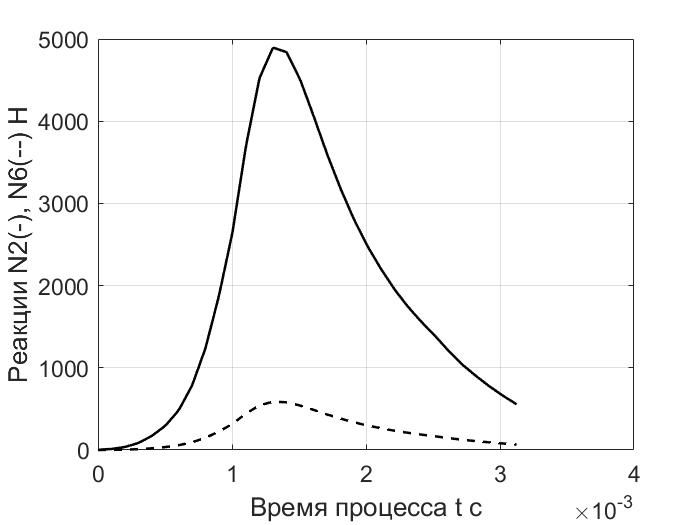
Рис. 6. Зависимость реакций N2, N6 от времени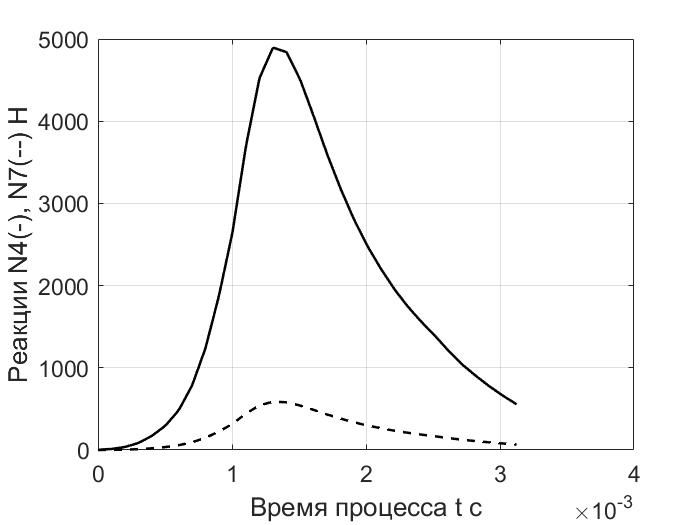
Рис. 7. Зависимость реакций N4, N7 от времени
Результаты расчета показывают работоспособность разработанного программного обеспечения и дают достаточно полное представление об особенностях динамики механизма. Величины нормальных реакций (рис.4-7) могут быть использованы для оценки прочности деталей механизма. Отметим, что в процессе движения (примерно при t = 2,28*10-3 с) значение вариантного индекса i поменялось с 1 на 2.
