Математическое моделирование параметрических термомеханических колебаний

Будем считать цилиндрический нагреватель тонким, если глубина проникновения в материал тепловых волн больше его диаметра d 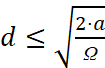[1]:

,    (1)

где a – температуропроводность материала,

Ω – частота температурных возмущений.

Если такой нагреватель подвергнуть периодическим термическим возмущениям, то его температура будет изменяться по периодическому релаксационному закону. При этом сам нагреватель будет испытывать периодические механические воздействия, обусловленные модуляцией натяжения s(t) за счет термического удлинения. Если частота Ω изменений натяжения будет связана с собственной частотой w поперечных вибраций нагревателя соотношением 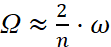[2]

,     (2)

где n=1, 2, 3 ,… , натуральное число,

то он может совершать поперечные параметрические вибрации, называемые термомеханическими колебаниями (ТМК) [3, 4].

В настоящее время известны лишь соотношения между порядком резонанса n и глубиной модуляции k колебательного параметра, в данном случае натяжения, при которых возникают параметрические колебания, она иллюстрируется диаграммой Айнса-Стретта [2]. Тем не менее, очень важной является функциональная зависимость амплитуды ТМК от глубины модуляции, соотношения между частотами Ω и w, которую прямыми опытами можно получить лишь с большими погрешностями.

Для нахождения указанной функциональной зависимости численным методом решено обобщенное уравнение динамики параметрических колебаний.

Будем считать вязкое трение линейно зависящим от средней скорости нагревателя, возвращающую силу, подчиняющуюся соотношению вида

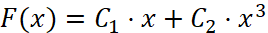, (3)

что подтверждается прямыми опытами. Тогда уравнение Матьё [2]

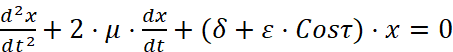    (4)

запишется в виде

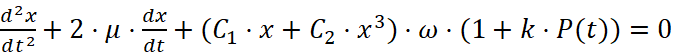.    (5)

Вышеприведенное уравнение (5) решалось численным методом с применением оператора OdeSolve программы MathCAD. Функция P(t) соответствовала релаксационному закону модуляций колебательного параметра [6] соответствующему закону изменения температуры. При решении релаксационная функция раскладывалась в ряд Фурье указанной программой до 21 гармоники включительно.

В начальных условиях (при t=0) задавалась амплитуда 0.01 условной единицы на уровне малых возмущений, второй опорной точке через время одного периода t=2×p¤w соответствовала амплитуда, большая начальной на величину, определяемую известным из [4] условием.

Численные исследования показали, что выбор амплитуды второй опорной точки влияет лишь на начальные стадии параметрической раскачки ТМК, но совершенно не влияет на установившуюся амплитуду. Результаты численных расчетов установившейся амплитуды показаны на рисунках 1–3.

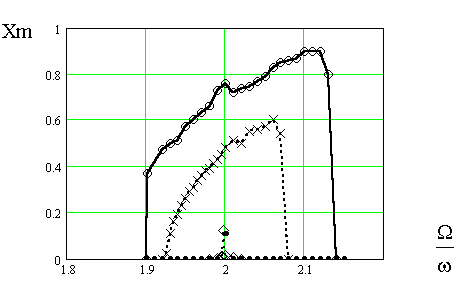
Рис. 1. Зависимость амплитуды ТМК первого порядка от соотношения основной и модулирующей частот и глубины модуляции. Глубина модуляции составляет: кривая ○ – 0,7; кривая × - 0,35; кривая <> - 0,05

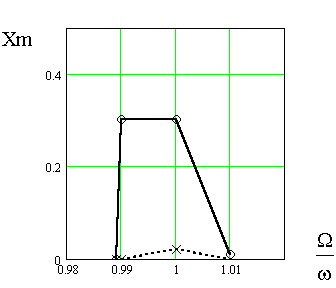
Рис. 2. Зависимость амплитуды ТМК второго порядка от соотношения между модулирующей и основной частотами. Глубина модуляции составляет: кривая для кривой ○ – 0,7; для кривой × - 0,25

Как видно из рисунка 1, для первого порядка, при глубинах модуляции от 0,05 до 0,1 параметрическое усиление наблюдается при условии Ω=2⋅ω, ширина области неустойчивости крайне мала, но она растет по мере возрастания глубины модуляции, что сопровождается также смещением частоты модуляции, соответствующей максимуму амплитуды ТМК в область более высоких частот, по всей видимости, из-за нелинейностей.

Аналогичная ситуация имеет место и для второго порядка, однако порог параметрического усиления соответствует большей глубине модуляции, а области неустойчивости значительно уже, чем для первого порядка – рисунок 2. При более высоких порядках резонанса (n больше 2) амплитуда ТМК резко падает.

Сравнение рисунка 3 с диаграммой Айнса-Стретта показывает, что области параметрического усиления при релаксационном типе модуляций оказываются значительно уже, чем при модуляциях типа меандра и гармонических. Как оказалось, отсутствует также область параметрической неустойчивости вблизи n=0,5, что, по всей видимости, связано с наличием сил вязкого трения.

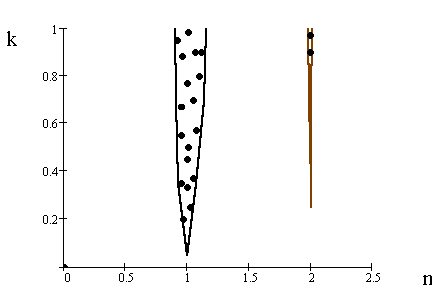
Рис. 3. Области неустойчивости (показаны точками), соответствующие параметрическому усилению термомеханических вибраций

Зависимости амплитуды ТМК от частоты  модуляции параметра для первого порядка можно выразить эмпирическим соотношением

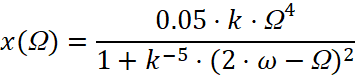.     (6)

Численным решением получены временные соотношения между модулирующими и основными колебаниями и зависимость амплитуды от времени на различных стадиях от начала до стационарного режима колебаний – рисунок 4. Из него следует, что установлению стационарной амплитуды ТМК первого порядка предшествуют участки биения, фиксируемые также экспериментально [6]. Модулирующие колебания s(t) опережают основные x(t) на угол 115° при втором и на угол 240° при первом порядках резонанса, что, по всей видимости, обуславливается формой модуляций натяжения проволоки.

Обнаруженные закономерности могут быть полезны в областях техники, где элементы устройств находятся под действием периодических температурных возмущений и для теории параметрических колебаний.

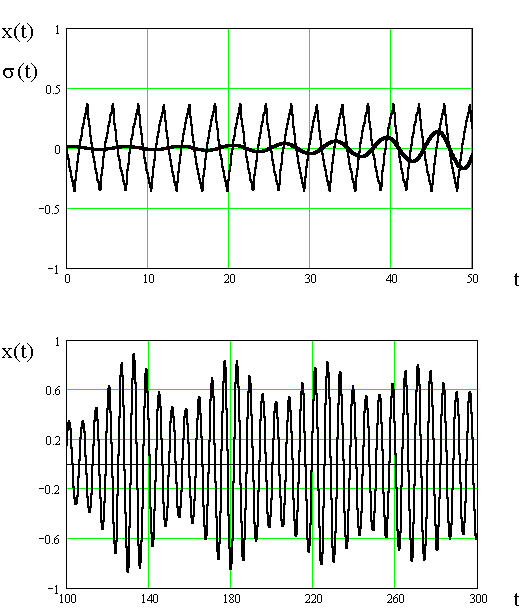
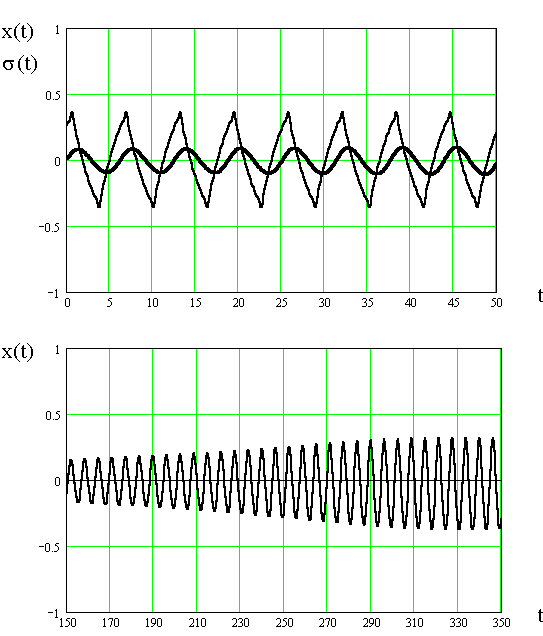
Рис. 4. Временные соотношения между релаксационными модулирующими s(t) и основными x(t) колебаниями для ТМК первого (два верхних графика) и второго порядков. Время и амплитуда отложены в условных единицах, глубина модуляции k=0,35