Задание 1. Упростить выражение: 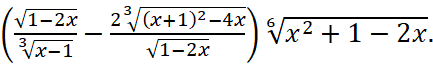
Решение. В этом задании проверяются следующие навыки ученика:
- Правильно упрощать выражение, содержащее корень n-ой степени,
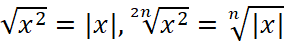 и тому подобное, то есть
и тому подобное, то есть 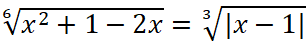 ;
; - Правильно раскрывать модуль, с учетом условия, |x-1|=1-x, так как, x<1/2;
- Правильно вносить отрицательный знак, находящийся перед дробью, в ее числитель, например,
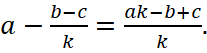
В результате один из вариантов правильного упрощения исходного выражения выглядит так:
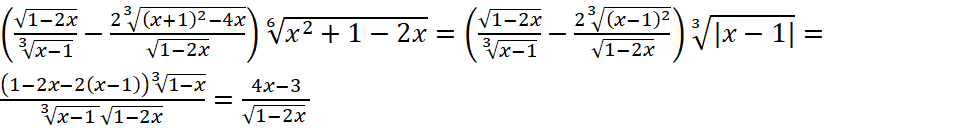 .
.
Замечание. Множество определения исходного выражения совпадает с множеством определения конечного выражения.
Ответ. 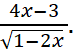
Задание 2.
Упростить выражение до одной функции и константы: 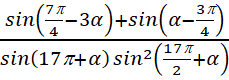 .
.
Решение. В этом задании проверяются следующие навыки ученика:
- Правильно применять формулы приведения,
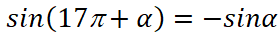 и
и 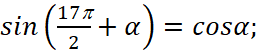
- Правильно применять формулы суммы (разности) синуса и косинуса, синуса двойного угла,
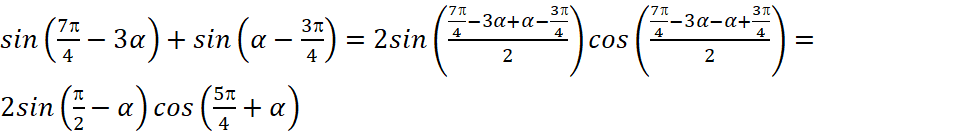 ;
;
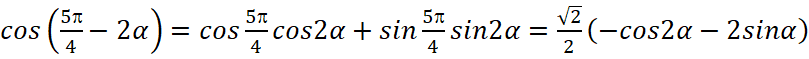 .
.
В результате, один из вариантов правильного упрощения исходного выражения выглядит так: 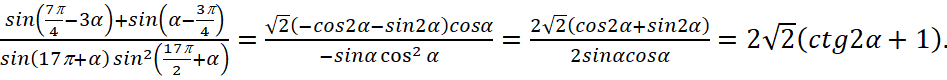
Замечание. Множество определения исходного выражения совпадает с множеством определения конечного выражения.
Ответ. 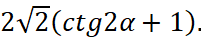
Задание 3. Решить неравенство: 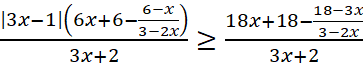 .
.
Решение. В этом задании проверяются навыки ученика при решении неравенства обобщенным методом интервалов:
1. Все выражения переносятся в одну, например, левую часть неравенства 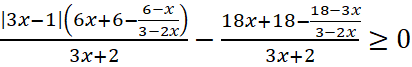 ;
;
2. Дроби приводятся к общему знаменателю 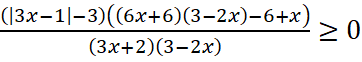 ;
;
3. Числитель полученной дроби раскладывается на множители 3x-1-34x+33x-43x+22x-3≥0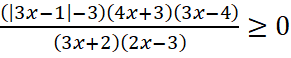 .
.
Нули сомножителей и числителя:
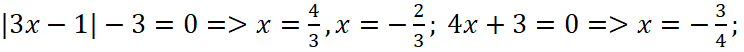
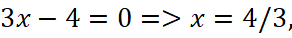
и знаменателя 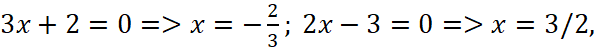 расставляются на числовой оси.
расставляются на числовой оси.
4. Определяются знаки полученных промежутков (рис. 1).
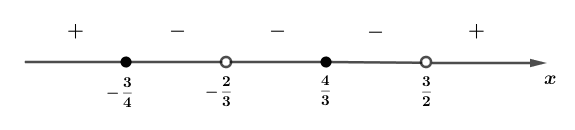
Рис. 1
Выписывается ответ 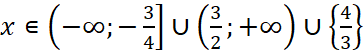 .
.
Замечание. Проверяется умение решать уравнения с модулем: |3x-1|-3=0.
Ответ. 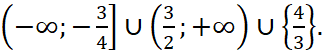
Задание 4. Решить неравенство: 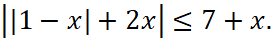
Решение. При решении неравенства будем использовать равносильные переходы:
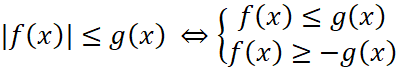 ,
, 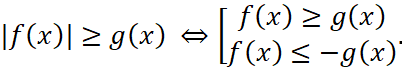
Получим следующее решение:
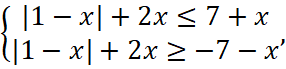
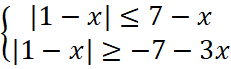 ,
,
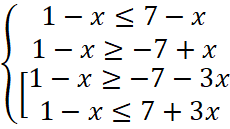 ,
,
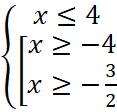 ,
,
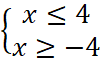 .
.
Ответ. 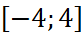
Задание 5. При каких значениях a прямые 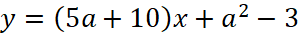 имеют хотя бы одну общую точку с отрицательной ординатой?
имеют хотя бы одну общую точку с отрицательной ординатой?
Решение. Так как в задаче идет речь об общей точке прямых, то исследуем пересечение этих прямых. Для этого рассмотрим линейное уравнение с параметром:
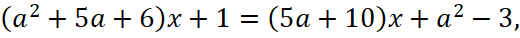
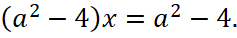
1. Если 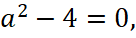 то уравнение имеет вид 0∙x=0, следовательно, прямые совпадают. Уточним уравнение прямой, с которой совпадут прямые из условия. При a=2 уравнение этой прямой y=20x+1 и на этой общей прямой есть хотя бы одна общая точка с отрицательной ординатой. Следовательно, значение параметра a=2 включается в ответ.
то уравнение имеет вид 0∙x=0, следовательно, прямые совпадают. Уточним уравнение прямой, с которой совпадут прямые из условия. При a=2 уравнение этой прямой y=20x+1 и на этой общей прямой есть хотя бы одна общая точка с отрицательной ординатой. Следовательно, значение параметра a=2 включается в ответ.
При a=-2 уравнение соответствующей прямой y=1. В этом случае на общей прямой все точки с положительной ординатой. Следовательно, значение параметра a=-2 не включается в ответ.
2. Если 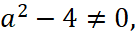 то x=1 - абсцисса общей точки прямых из условия, а ордината общей точки
то x=1 - абсцисса общей точки прямых из условия, а ордината общей точки 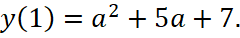 При всех значениях a:
При всех значениях a: 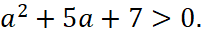 Следовательно, при рассматриваемых значениях параметра a ордината общей точки прямых положительная и в ответ ни одно из рассматриваемых значений параметра не попадает.
Следовательно, при рассматриваемых значениях параметра a ордината общей точки прямых положительная и в ответ ни одно из рассматриваемых значений параметра не попадает.
Ответ. 2.
Задание 6. В треугольнике ABC на стороне AB взята точка D, а на стороне BC точки E и F так, что AD:DB=3:2, BE:EC=1:3 и BF:FC=4:1, прямые AE и FD пересекаются в точке O. Найти площадь треугольника FOE, если площадь треугольника FDB равна 224.
Решение.
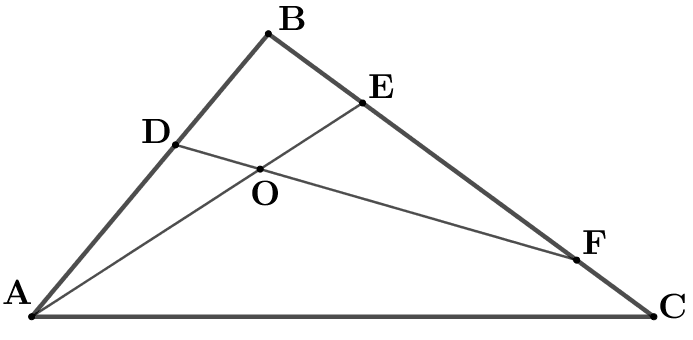
Рис. 2
Треугольники FOE и FDB имеют общий угол (рис. 2), поэтому 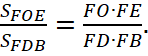 Из этого равенства, зная
Из этого равенства, зная 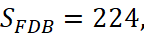 найдем
найдем 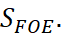 Осталось только определить отношения
Осталось только определить отношения 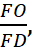
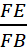 .
.
1. Найдем сначала 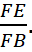 По условию
По условию 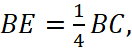
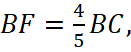 следовательно,
следовательно,
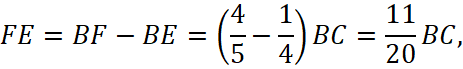
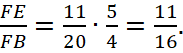
Заметим, что нам известно и такое отношение 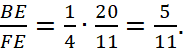
2. Найдем отношение 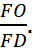 По теореме Менелая для треугольника FDB и секущей AE получаем:
По теореме Менелая для треугольника FDB и секущей AE получаем: 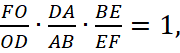
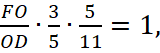
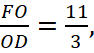 следовательно,
следовательно, 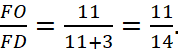
3. Теперь можно найти 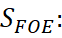
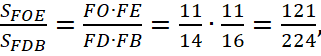
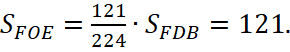
Ответ. 121.
Задание 7. Решите уравнение: 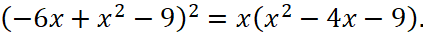
Решение. 1 способ. Замена: 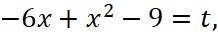 тогда
тогда 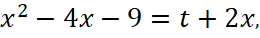 уравнение можно записать в виде
уравнение можно записать в виде 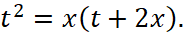 Рассмотрим уравнение как квадратное относительно t:
Рассмотрим уравнение как квадратное относительно t:
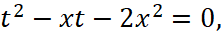
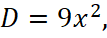
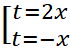 .
.
Тогда 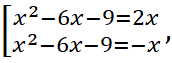
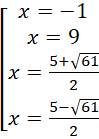 .
.
2 способ. x=0 не решение уравнения. Разделим обе части уравнения на x2, чтобы прояснить схожесть частей уравнения: 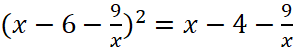 . Пусть
. Пусть 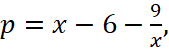 тогда
тогда 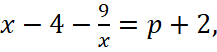 уравнение можно записать в виде
уравнение можно записать в виде 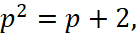
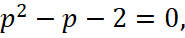 следовательно
следовательно 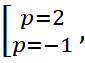
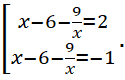 Получаем два квадратных уравнения, как и в 1 способе.
Получаем два квадратных уравнения, как и в 1 способе.
Ответ. 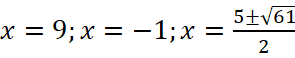 .
.
Задание 8. Найдите значения параметра a, при которых уравнение
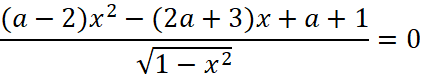
имеет два различных решения.
Решение. ОДЗ: 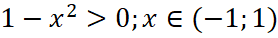 . Обозначим
. Обозначим
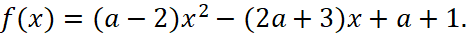
1) Линейный случай: a=2. Выражение для f(x) примет вид -7x+3. Решение уравнения 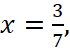 таким образом a=2 не подходит, так как решение уравнения только одно.
таким образом a=2 не подходит, так как решение уравнения только одно.
2) Пусть a≠2. Опишем параболы, которые соответствуют двум различным решениям на интервале (-1;1): 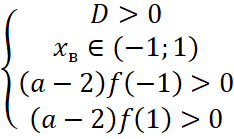 . Решая систему, получаем
. Решая систему, получаем 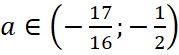 .
.
Ответ. 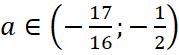 .
.
Задание 9. Дан ромб ABCD, ∠BAD=60°, AD=2a. Вне плоскости ромба взяли точку T так, что отрезок TK перпендикулярен плоскости ромба, TK=a. Точка K - середина стороны BC, точка N - середина отрезка BT, точка M - середина отрезка DT, точка L - середина отрезка DC. а) Исследуйте взаимное расположение прямых AN и ML, обоснуйте свои выводы с помощью теоретических фактов и вычислений. б) Найдите угол между прямыми AN и ML. в) Найдите угол между прямой BD и плоскостью BTC. г) Найдите расстояние от точки N до прямой DC.
Решение. 1 способ. Достроим пирамиду TABCD. ∆AML - сечение пирамиды (рис. 3), N∉(AML), (ML)⊂(AML), (AN)∩(AML)=A и A∉(ML). По признаку скрещивающихся прямых - прямые AN и ML скрещиваются. Способ быстрый, но не приближает к нахождению угла между прямыми.
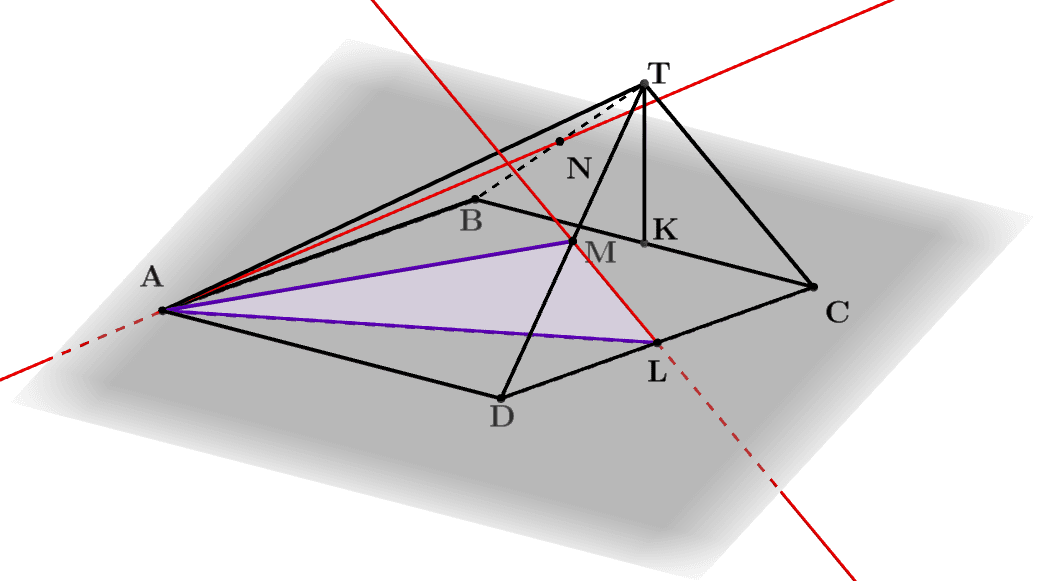
Рис. 3
2 способ. Построим прямую пересечения l плоскостей ABT и DCT. Так как AB параллельна CD, то и l∥AB, l∥CD (рис. 4).
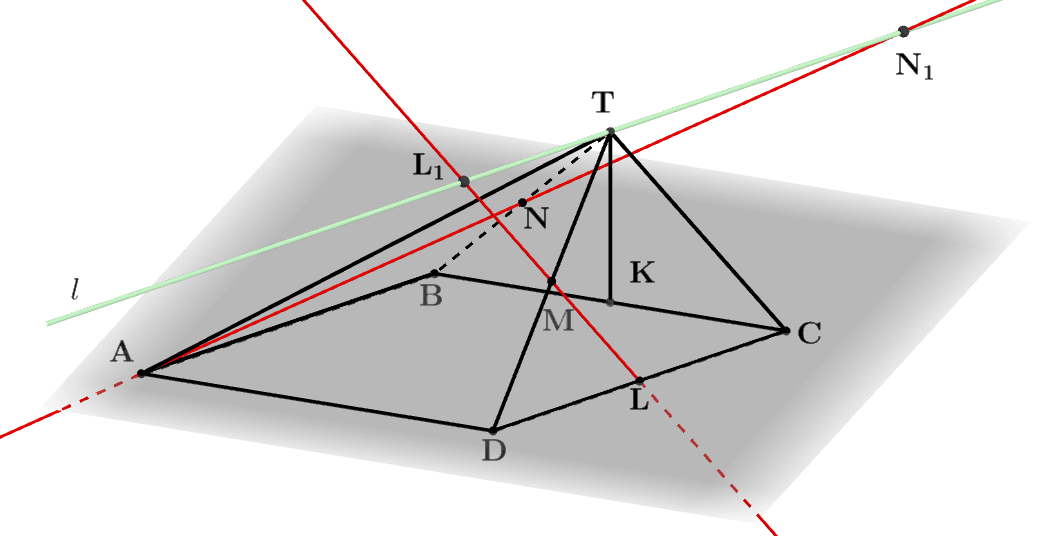
Рис. 4
Если наши прямые и пересекаются, то на прямой l. Пусть 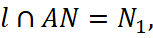 тогда
тогда 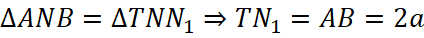 (рис. 5).
(рис. 5).
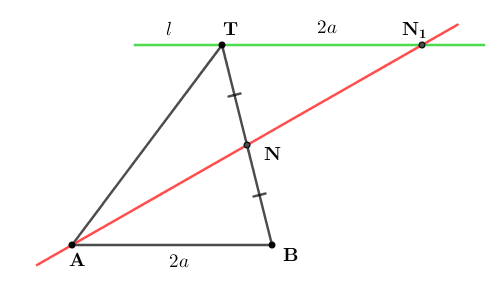
Рис. 5
Пусть l∩LM=L1, тогда 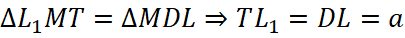 (рис. 6).
(рис. 6).
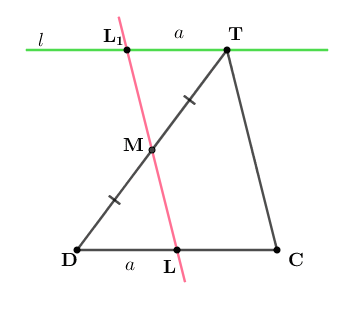
Рис. 6
Так как 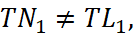 то N1≠L1. Далее, AN⊂(ABT), LM∩(ABT)=L1, L1∉AN и, по признаку скрещивающихся прямых, прямые AN и ML скрещиваются.
то N1≠L1. Далее, AN⊂(ABT), LM∩(ABT)=L1, L1∉AN и, по признаку скрещивающихся прямых, прямые AN и ML скрещиваются.
б) Проведем 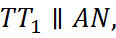 тогда
тогда 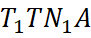 - параллелограмм по определению и
- параллелограмм по определению и 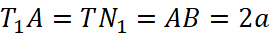 (рис. 7).
(рис. 7).
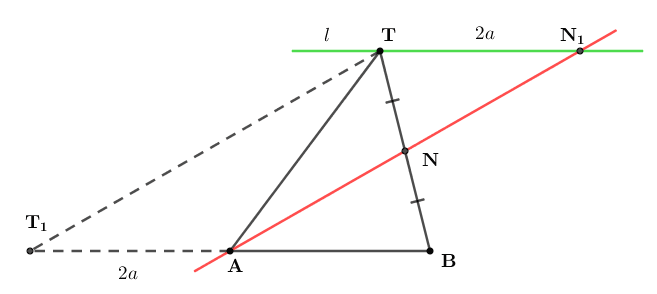
Рис. 7
Найдем угол между прямыми AN и ML. Так как TC∥ML, то 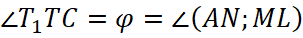 или смежному с ним (рис. 8).
или смежному с ним (рис. 8).
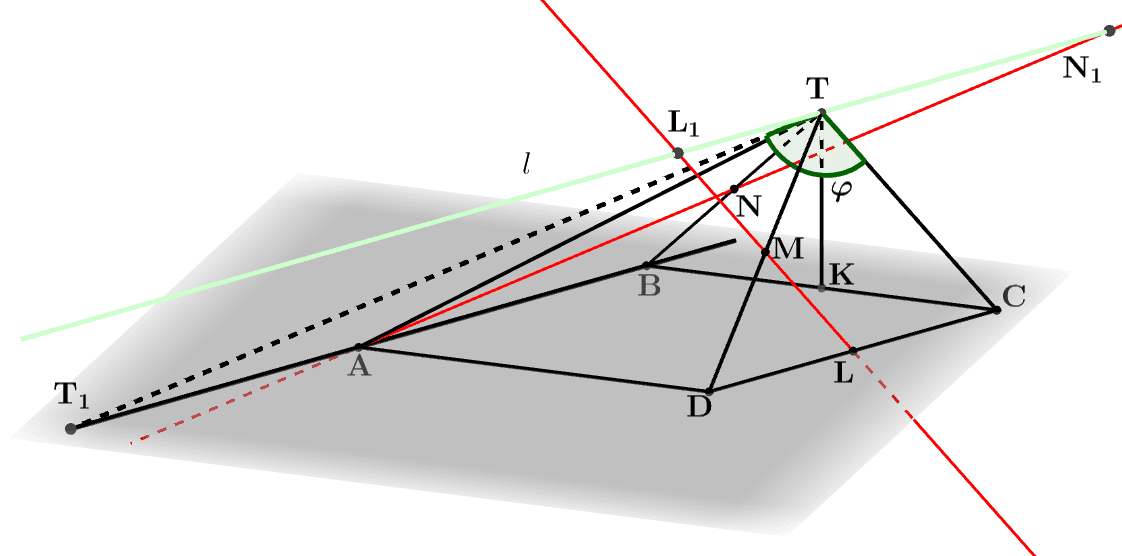
Рис. 8
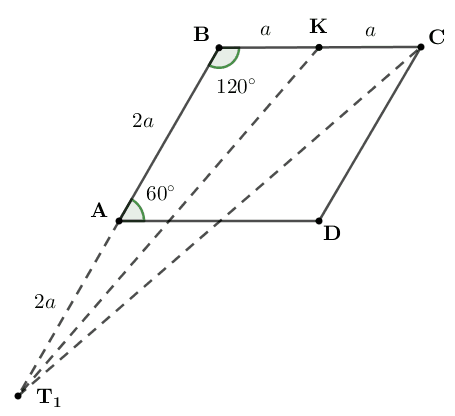
Рис. 9
По теореме косинусов в 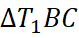 (рис. 9):
(рис. 9): 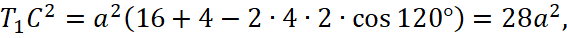 по теореме косинусов в
по теореме косинусов в 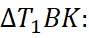
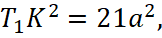 по теореме косинусов в
по теореме косинусов в 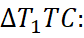
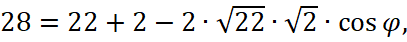 Следовательно,
Следовательно, 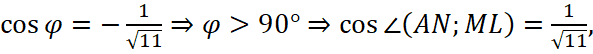 окончательно получаем ответ
окончательно получаем ответ 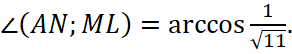
Ответ. 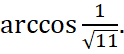
в) Найдем угол между прямой BD и плоскостью BTC. Для этого найдем угол между прямой BD и ее ортогональной проекцией на плоскость BTC (рис. 10).
Докажем, что DK⊥BTC. Действительно, так как BC=CD=2a, то ∆BCD – равнобедренный, ∠BCD=60°, следовательно, в ∆BCD все углы по 60°, и он является правильным. Тогда медиана DK является и высотой: DK⊥BC. Далее, по условию TK⊥ABC и в силу DK⊂(ABC) получаем, что TK⊥DK. Таким образом, прямая DK перпендикулярна двум пересекающимся прямым BC и TK в плоскости BTC, что и означает по признаку перпендикулярности прямой и плоскости перпендикулярность прямой DK и плоскости (BTC).
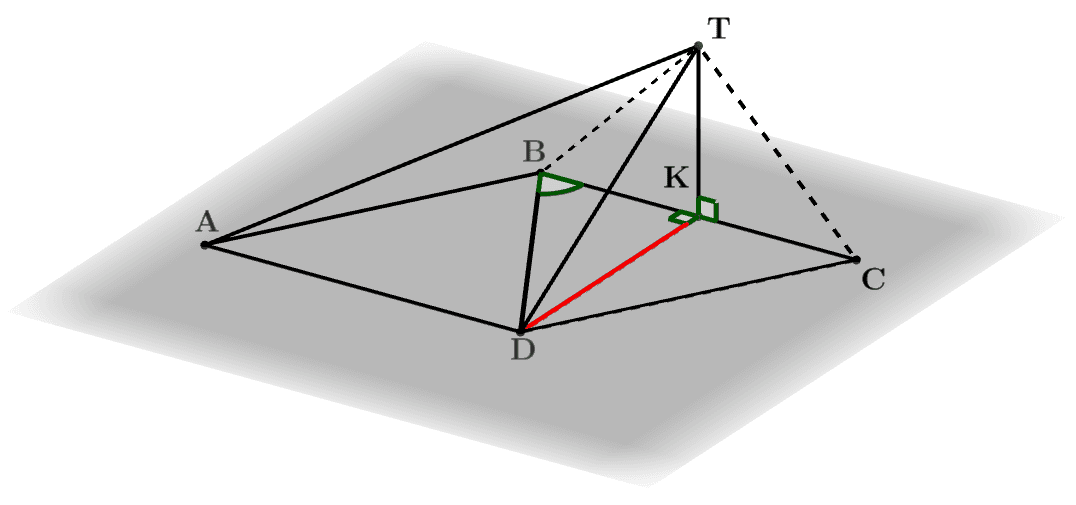
Рис. 10
Следовательно, проекцией BD на плоскость BTC является BK и угол между BD и плоскостью BTC есть ∠CBD=60°.
Ответ. 60°.
г) Найдем расстояние от точки N до прямой DC (рис. 11).
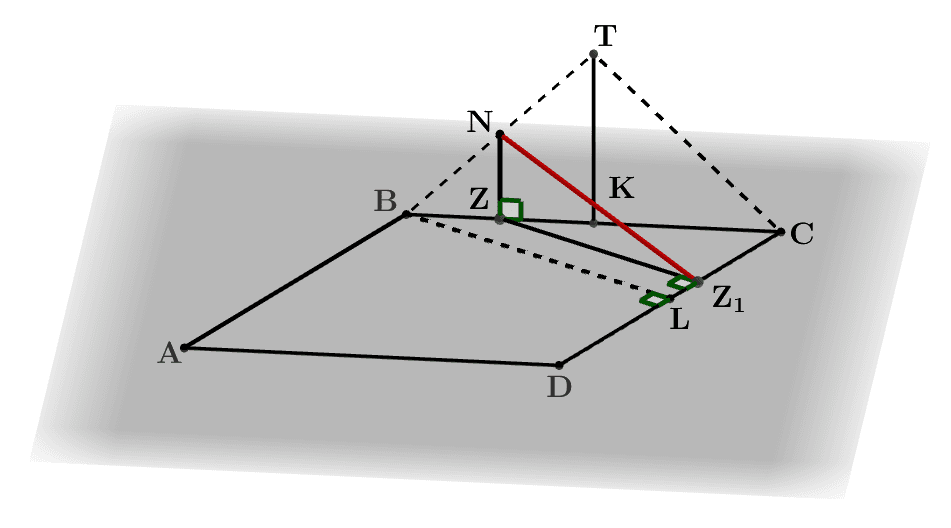
Рис. 11
Пусть Z - середина BK, тогда NZ – средняя линия в треугольнике BTK, 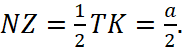 Далее, NZ∥TK, поэтому NZ⊥(ABC). Следовательно, Z – проекция точки N на плоскость ABC.
Далее, NZ∥TK, поэтому NZ⊥(ABC). Следовательно, Z – проекция точки N на плоскость ABC.
Пусть ZZ1∥BL, где Z1∈DC. Так как BL медиана, следовательно, и высота в правильном треугольнике BDC, то ZZ1⊥DC и ZZ1 – проекция NZ1 на плоскость ABC. Тогда по теореме о трех перпендикулярах NZ1⊥DC и, следовательно, расстояние от точки N до прямой DC равно длине NZ1.
Найдем NZ1 из прямоугольного треугольника NZZ1. Так как 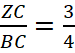 и
и 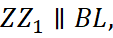 то из подобия треугольников CZZ1 и CBL получаем
то из подобия треугольников CZZ1 и CBL получаем 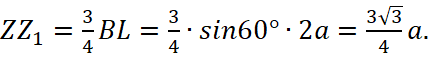 Окончательно,
Окончательно, 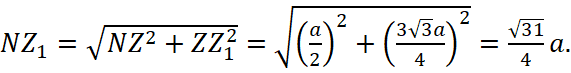
Ответ. 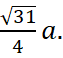

.png&w=640&q=75)