It is clear that the lack of understanding of real physical processes, which rely on the logic of construction from simple to complex view with the exception of miracles, could not give a correct mathematical modeling of the interaction in the atom. Therefore, the scientists proposed the fitting variants of mathematical models, which, due to the fitting, matched the practical results. The mistake of scientists was not conclusion that they used a mathematic fitting for the result, but condition of mistake was the fact that they, having received some coincidences with practice, based on these mathematical models, drew conclusions about physical processes in the atom with the presence of miracles. Next, we will show what paradoxes were in the fitting models of scientists, and how the same practical results we obtained without adjusting to the result on the base of our theory.
Let's start with the question: "Why did physics come to the teleportation, Heisenberg uncertainty relation, probabilistic wave functions for orbitals and excluded the physical laws of the macrocosm in relation to the using in the microcosm?".
The initial idea of describing the rotation of an electron around a proton was connected with a planetary model and a well-known equation from classical physics was taken [1]:
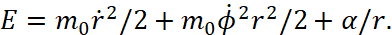(1)
We note that this equation was taken as a prototype for describing the probabilistic wave condition of a particle in the theory of a hydrogen-like atom [2]. At the same time, of course, there were paradoxes, which we will also describe below. Here, the motion of the particle, in the case of force of attraction, according to the classics is described by the trajectories shown in Fig. 1.
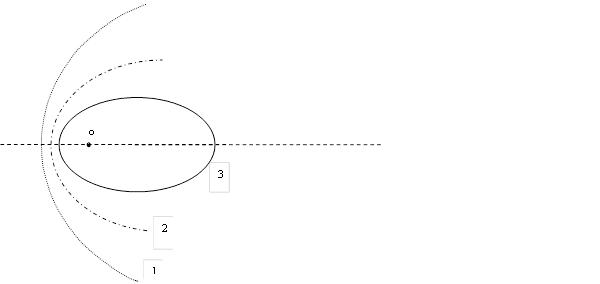
Fig. 1. Trajectories of motion of particle as a function of velocity in the case of the force of attraction of the particle to the center of coordinates ‒ O
Accordingly, it is assumed that for E > 0 the trajectory turns out to be a hyperbola (line 1), for E = 0 the trajectory will be a parabola (line 2). If a particle starts its motion from a place of rest into infinity, then this case of parabola will occurs. Finally, when E< 0, the trajectory will be an ellipse (line 3).
At the magnitude of the energy E and the moment of momentum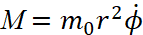 
, according to the condition
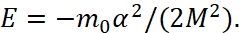(2)
the ellipse turns into a circle. We need to understand why this conclusion turned out. This is due to the condition that the formula (1) has been replaced with a completely other equation, in which the derivative along the length r is zero, and the significance of the angular momentum is being considered to be some constant magnitude which is independent from distance, and we get:
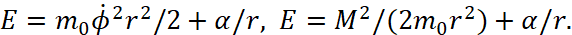(3)
Here we have α<0. It should also be noted that in the second equation (3) scientists use the moment of impulse M as magnitude which has the varying from distance depending on 1/r2, while in the magnitude of the moment of impulse there is already a member proportional to r2. That is, scientists changed the law of physics to inversely proportional, without any justification. From the point of view of physics, at E = 0 we get equality between potential and kinetic energy. If E is not equal to zero, then, according to the Hamilton-Jacobi equation, there must be radial motion with energy E = m0vr2/2, otherwise we must admit that this energy arose by a miracle and does not belong to kinetic or potential energy. However, it is this significance of the difference between kinetic and potential energy that is further used and the concept of Uэфф = Е is being introduced, and it is being shown in Fig. 2.
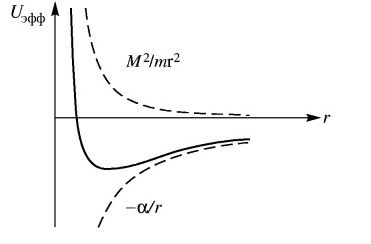
Fig. 2. Value graph of Uэфф= Е
Equation (3) is actually a quadratic equation with respect to 1/r. From here we have a solution in the form:
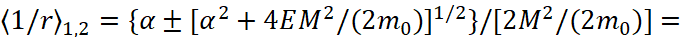
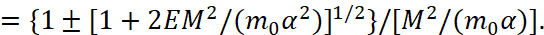(4)
We will introduce the notation:
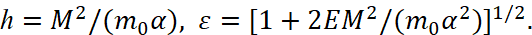(5)
We note that E < 0, ε<1. Using these new notations, the two roots of the quadratic equation can be represented as:
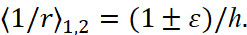(6)
Hence the minimum and maximum distances from the center of the field of attraction are equal:
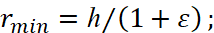
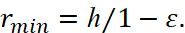(7)
The obtained conditions are shown in Fig. 3.
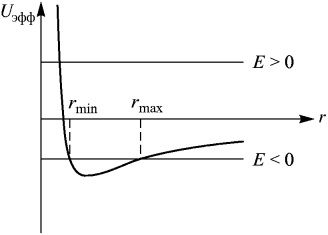
Fig. 3
The case for ε=0, obviously, corresponds to motion along a circle, while the energy E is not zero (Fig. 4).
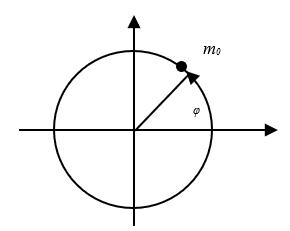
Fig. 4. The motion of an electron in a circular orbit through generalized coordinates
Why do we see the paradoxical solution of the resulting quadratic equation when a particle has motion along an orbit?
The first reason is that with the dynamics of motion along the orbit according to the equation of the harmonic oscillator (1), the orthogonal vector significances of the kinetic energy velocities vary in coordinates according to the laws of sine and cosine, and only in this case the modulus of the sum from quadratic magnitudes remains unchanged, and then we have a reflection of the energy significance E as the magnitude of the quantitative exchange between potential and kinetic energies [3].
It should be noted that in the theory of a linear harmonic oscillator [3], the member with the angular momentum acts as the attractive force from potential energy. However, in the formula (3), physicists removed the radial significance of velocity, and we have here a centrifugal force, which has compensation by the force of Coulomb's attraction, and these forces are directed in the opposite direction to each other. It is clear that equality of forces means equality of energies, but here we have inequality due to the magnitude of E and this means a paradox. The second paradox is that the moment of impulse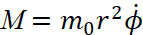 
varies directly proportionally to the magnitude of r2, but mathematically it has been turned into a quantity that has an inversely proportional dependence on 1/r2, and hence moment of impulse is some magnitude of constant. The third paradox concerns the combination of the first two in the calculation of a fictitious magnitude Uэфф = Е to obtain a pit with possible equality at two magnitudes of the minimum and maximum radius of orbits. In other words, we have a variant of the ambiguity of the relation of potential and kinetic energy. Scientists can't do without miracles here, and it turns out that two plus two is not equal to four. Actually, this miracle was realized due to the introduction in quantum mechanics of a probabilistic wave function for the location of an electron in an atom in the form of orbitals with movement due to teleportation [2]. However, in this case, the centrifugal force should be forgotten.
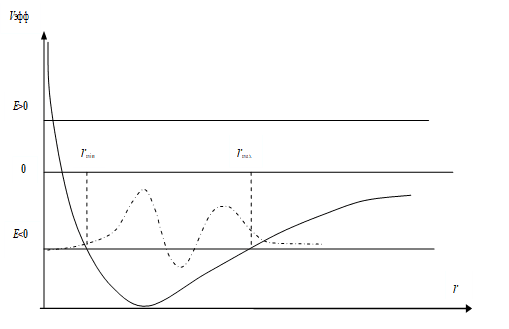
Fig. 5. Graph of the dependence of the effective potential energy (solid curve) from the distance. The dashed dot curve shows the course of the wave function
Thus, the problem of the connection of kinetic and potential energy was realized by the method of fitting to the result. Note that if we proceed from the equality of the energy of the centrifugal force and the energy of the force of Coulomb [4], then we have the equality:
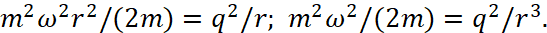(8)
If we assume that 
, then in this case we have a graph of dependencies shown in Fig. 6.
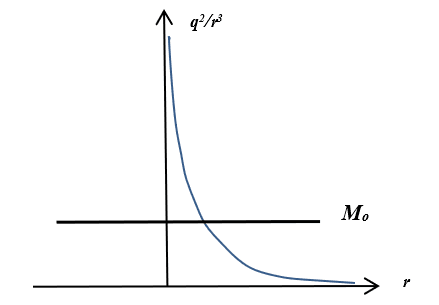
Fig. 6. Graphs of the dependences of the force energy of Coulomb and the centrifugal force energy
Accordingly, according to the second formula (8), we have a circular orbit with a radius at the intersection point of the graphs at one single magnitude depending on ω2. It should be taken into account that the angular velocity determines the kinetic energy of the particle, in depending on the radius of the orbit. And in this case, we have an increase in kinetic energy proportional to the value of ω2r2. At the same time at small magnitudes of angular velocity, but with account of a large radius, the moment of momentum (in depending on distance) varies over the parabola according to the graph (Fig. 7).
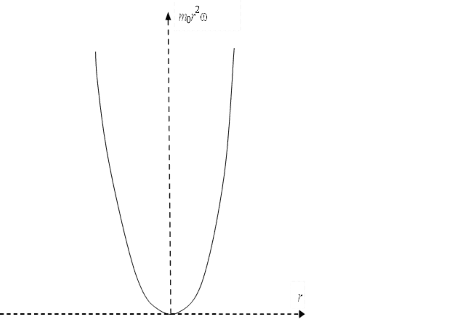
Fig. 7. Graph of the angular momentum depending on the distance
It is clear that we have a paradox when equating according to the formulas (8), because when the distance increases, the magnitude of the radial velocity change from the center of attraction will decrease (ω=const) with dropping the centrifugal force, and this just allows the Coulomb forces to keep the electron in orbit at large distances with exception of falling on nucleus, although the orthogonal component will increase in proportion to the magnitude of the angular momentum and it is practically a linear velocity of motion (the second formula in (8) and the graph is Fig. 6). However, according to the graph in Fig. 7, we have a variant in which the centrifugal force should increase depending on the distance (otherwise the force and energy are not related), and the Coulomb force should has the decreasing depending on the distance (it is first formula (8)). This would mean that there is a distance from which the centrifugal force exceeds the Coulomb force and the influence of the Coulomb force is zero. On this basis, a potential barrier extending to infinity for a harmonic oscillator is constructed in quantum mechanics. In this case, the Coulomb force is replaced by centrifugal force, and it also means a paradox, since these are opposite forces to each other and their interchangeability is not determined by anything.
Therefore for excluding of paradoxes and because an electron and a proton as opposites should be a closed system through exchange, with a stable condition and the presence of attractive forces, it is necessary to represent kinetic energy in the form of equivalent potential energy by changing the observation system. Such a replacement is possible only in our theory, where the Lorentz force reflects the centrifugal force and this force is the Coulomb force in the opposite observation system, connected to our system through the speed of light [5]. In this case, they can be compared. Actually, such an approach is determined by the subordination of the forces of the Coulomb and Lorentz to SRT of Einstein in the form of: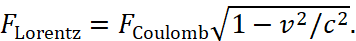 
This formula determines the electromagnetic continuum which has connection with spatial temporary continuum. And this is exactly what was done intuitively in quantum mechanics by Bohr in the following way. The Bohr obtained the condition for stationary orbits based on Planck's postulate, according to which only such states of the harmonic oscillator are realized whose energy is equal to:
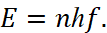(9)
Here n is an integer. Hence, according to the Bohr and Planck condition, the equation [6] is taken for stationary orbits in the view:
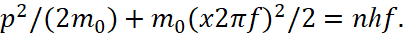(10)
At the same time, it is assumed that there is no radiation on the base of the following postulates of Bohr [7]:
- Out of an infinite set of electronic orbits possible from the point of view of classical mechanics, only some discrete orbits satisfying certain quantum conditions are actually carried out. An electron in one of these orbits, despite the fact that has moving with acceleration, does not emit electromagnetic waves (light).
- Radiation is emitted or absorbed in the form of quantum of energy of a light hf during the transition of an electron from one stationary (stable) state to another. The magnitude of quantum of the light is equal to the difference in the energies of those stationary conditions between which the quantum leap of the electron takes place:
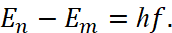(11)
It is clear that the presence of discrete energy levels and orbits, respectively, is determined by the presence of a minimum magnitude in the form of Planck's constant (h). However, the change in the state of the electron when moving along the orbit occurs always, and the cancellation by Bohr of the condition of radiation and of absorption due to the motion with acceleration is caused only by the fact that he failed to solve the problem of electrodynamics to replenish the electron energy due to the fact that the change of direction leads to the absorption of energy for a new direction. In other words, Bohr did not know how the replenishment of energy took place, so he imposed a ban on radiation, since continuous radiation must inevitably lead to the loss of energy by the electron, and hence we have the inevitable fall of the electron on the nucleus, which is not being observed. Therefore, Bohr's mistake lies in the fact that he did not solve the problem of replenishing energy of an electron, but acted simply by inventing a ban on radiation, but at the same time he introduced a difference between the components of kinetic energy through an amount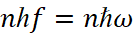 
according to the formula (10), that is, he actually used the equation of a circle. However, here all magnitudes are expressed in terms of kinetic energy, and the significance 
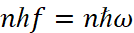can only reflect the magnitude of the kinetic energy of the photon. In fact, there are no forces of attraction for potential energy in the formula (10), since potential energy must be expressed through dependence on distance, and not on frequency, which is associated with centrifugal force. In the view of the prototype of the formula (10) with account of the potential energy, we can consider Einstein's formula at describing the photoelectric effect [8]:
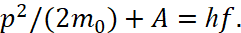(12)
Here A is the smallest potential energy that needs to be communicated to an electron in order to remove this electron from a solid or liquid body into environment. In this case, the potential energy A replaces the member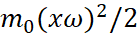 
in the formula (10), that is, 
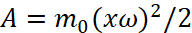. However, the difference here is that the formula (12) does not describe the stationary condition of rotation of an electron around a proton in orbit, but determines transition of electron from one state to another state due to the absorption of photon energy. Then, by virtue of identity, when replacing the centrifugal force with a real centripetal force, the formula (10) should also characterize the change of condition due to the radiation process, with falling of electron on the nucleus, if there is no mechanism for replenishing the energy of electron. However, the first postulate of Bohr is conclusion that an electron in one of the discrete orbits, despite the fact that it moves with acceleration, does not emit electromagnetic waves (light) [7]. That is, the scientists wanted and canceled rules, without explaining anything and throwing laws of electrodynamics, as they say, "not to rack head." Even schoolchildren studying physics for the first time are perplexed by this, but physicists are in no way worried about it, otherwise their entire "far-fetched" system will collapse, and this is fraught for many with the collapse of all their attempts in science. It is an explanation of the fact why all this takes place in science.
We will show the solution to this paradox with radiation and absorption in next articles, and now we will consider the further derivation in quantum mechanics of the rules for quantization of circular orbits based on a one-dimensional model. In this case, equation (10) can be written as:
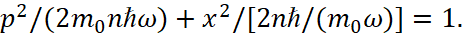(13)
If we consider the functional dependence and consider the magnitudes of p and x as orthogonal coordinates of the axes then from formula (13) the phase trajectory of the harmonic oscillator is an ellipse (Fig. 8).
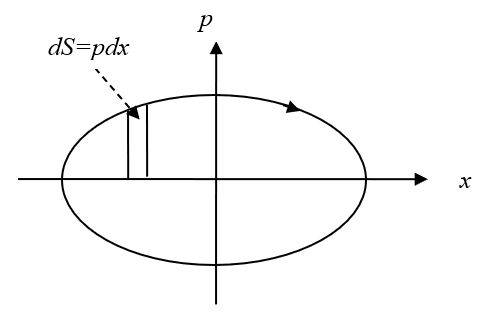
Fig. 8. Phase trajectory of the harmonic oscillator
The semi ‒ axes of the ellipse are equal:
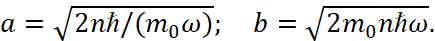(14)
The area of the ellipse is equal to significance of multiplication of the semi-axes with multiplied by π:
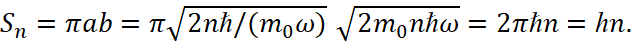(15)
In fact, taking into account the radiation, we have a Carnot cycle with quantization of the radiation energy in proportion to hn, i.e. from the introduced condition (9). In other words, a completely self-contained system of object with in the Universe is excluded. At the same time, we take into account that the closed system (13), which is characterized by an ellipse, does not consider the principle in the dynamics of radiation and absorption, in depending on the transformation of energies, but characterizes only the motion of the particle along the orbit without reference to the forces characterizing the change in the state of the particle along time. However, the area can be represented as:
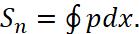(16)
Here, in process of integrating, we have the bypass of entire ellipse. The quantization rule follows from the comparison of expressions (15) and (16):
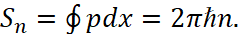(17)
The Bohr extended the rule (17) obtained for the harmonic oscillator to other mechanical systems. In particular, for an electron moving around the nucleus along a circular orbit (Fig. 4), he took the azimuth angle as the coordinate 
. The speed in this case will be the value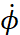 
. We know that with rotational motion, the role of linear velocity passes to angular velocity 
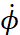, and the role of mass ‒ to the moment of inertia m0r2. Accordingly, the generalized impulse is equal to:
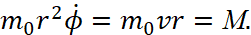(18)
The last expression defines the moment of the usual momentum M, taken relative to the nucleus. Thus, for an electron which has motion along a circular orbit, the condition (17) has the form:
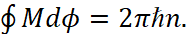(19)
The force with which the nucleus will act on the electron is central, so M = const, and the left part of the ratio (19) is equal 2πМ. Hence, we come to the condition:
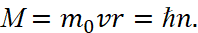(20)
It should be noted that the rule (19), which the Bohr extended to other mechanical systems, actually is being referred to the same mechanical system, namely to the rotation of the electron around the nucleus. But the fact is that it is not possible to obtain equations (10) and (13) from the formula (18), because the Bohr in (18) introduced actually a condition of the connection of length r in the view of potential energy, but velocity v reflects kinetic energy taking into account the inversely proportional dependence between of opposites. It is clear that the potential energy in (10) was not even considered. Or let the representatives of quantum mechanics show how this happens, but without the probabilistic approach adopted in their direction, which we assess as an attempt to "do fool" from the layman who is accustomed to trust the conclusions of such "pseudo luminaries" in science.
We state the fact that here we are dealing with the ambiguity of the representation of momentum and coordinate. In one case, the coordinate has a change, for example, the cosine in quadrate and the momentum is sine in quadrate and in the other case, and both the coordinate and the momentum have a linear change. How such a thing is possible, if we take a probabilistic approach, even the layman does not understand. However, the specified rule (20) can be obtained from the Louis de Broglie formula, which has been tested experimentally in practice, and this suggests that the obtained dependence reflects precisely the law of the inversely proportional relationship between kinetic and potential energy, regardless of the fitting option carried out by Bohr. Indeed, from argument of wave function of the Louis de Broglie follows the equation:
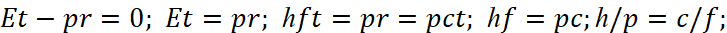(21)
Hence follows the derivation of the Louis de Broglie formula of the form:
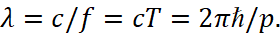(22)
Then, taking into account the condition r=ct=c/f (from the Minkowski geometry) for the Lorentz transformations [9], as well as taking into account that the opposites have an inversely proportional relationship and in addition the length and time in them have the change of places, and the linear change in one opposite looks like a closed change in the other opposite, we have:
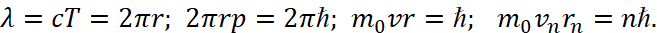(23)
Having intuitively obtained the law (23), scientist used it when finding Bohr orbits as follows. For the hydrogen atom, he chose the motion of an electron in the form:
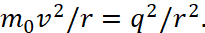(24)
Here q=e is the charge of the electron. In fact, he took equation (1) and at the same time equated the energy significance E = 0, doubled the kinetic energy magnitude, that is, he began to consider them not as opposites, and divided the members of equality onto the same magnitude equal to r. In fact, this is an equation of equality of kinetic energy and potential energy, where each of the energies reflects half of the total energy E of a common closed system of two opposites, and this corresponds to formula [5]:
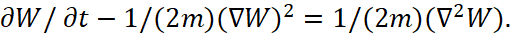(25)
At the same time, if ∂W/∂t=E=0, it means that the radiation energy nhf is equal to the absorption energy, and this is what ensures the equality of potential and kinetic energy. If we use equation (24) to calculate the radius of the orbit, then we get a paradox in which the greater the kinetic energy of the electron, determined by the velocity v, the smaller the radius of the orbit r. Therefore, the Bohr intuitively excluded the magnitude of velocity v from the equation, changing it to the opposite significance of r in accordance with (23). In fact, he introduced the representation of kinetic energy in the opposite observation system to obtain the equivalent of potential energy, that is, he brought action and reaction into the same quantitative representation, and obtained an expression for Bohr orbits:
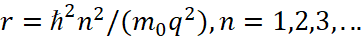(26)
Here, the greater the kinetic energy of the electron, which is determined by the value of n, the greater the radius of the orbit and this corresponds to practice. At the same time, the radius of the first orbit of the hydrogen atom was calculated and its value is equal to:
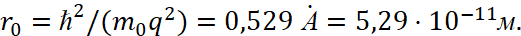(27)
In this case, the Bohr radius has a magnitude of the order of the gas kinetic dimensions of the atom. Next, scientists take into account that the electron radius is calculated by the formula [10]:
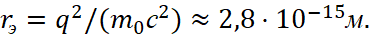(28)
In relative units, we will have the ratio of the first Bohr radius to the electron radius in the form:
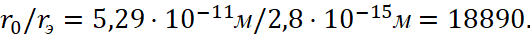(29)
However, let's find out the fitting principle in this method of determining Bohr orbits.
Here, the formula (26) includes the magnitude of kinetic energy which has direction perpendicular to the velocity and acceleration associated with the counteraction of the Coulomb force. In other words, there is no equality of the energy of Coulomb force with the energy associated with centrifugal forces (in fact, it is the Lorentz force), which corresponds to (8). On the base of the connection of kinetic and potential energy according to (8), we obtain the equation:
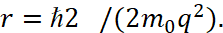(30)
The difference with (28) is obvious.
The second paradox here is related to the fact that the interaction of charges occurs through a medium (space-time curvature), however, in the CGS measurement system we have a completely the linearizing system outside the connection of space and time (to which we pay serious attention to all thoughtful readers so that the adjustments and artificially introduced "superstructures" are understandable) by Lorentz transformations, and this is expressed by a system of equations [11]:
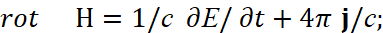
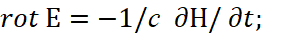
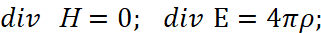(31)
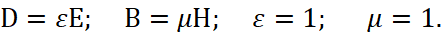
Here, the intensity of electrical induction differs linearly from magnetic induction at the speed of light without taking into account the environment. Therefore, we choose the MKSA system, in which the so-called "vacuum" is determined by the constants of electrical ε0 and magnetic μ0 permeability (these are what we associate with the change in space-time curvature), and we take into account the multiplier 4π, as in the CGS system (in this case, the charged particle has the same normalization with space and time):
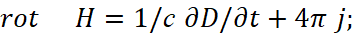
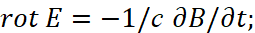
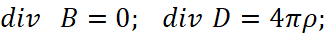(32)
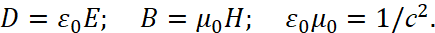
In this case, the Coulomb force and potential energy should be calculated using the formulas:
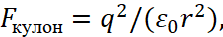(33)
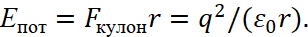
Next, let's remember that we excluded the magnitude of the impulse in (23), and took the equivalent in the form of a radius, which means a transition into the opposite. At the same time, the laws of SRT and GRT of Einstein remain the same, because the multiplication of these opposites is invariant and equal to a significance of constant, here the changes of the momentum and radius are being subordinated to SRT. Hence, the magnitude of the radius of the orbit must be calculated in accordance with the well-known formula [12] according to Einstein's SRT:
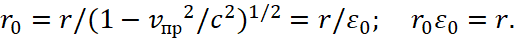(34)
Here vпр refers to the average integral velocity in the opposite observation system that is connected to the environment. We take into account that length and time are changing places in opposites, with account of their connection through the speed of light. In other words, we obtain the dependence of potential energy from the constant of electrical permeability in accordance with GRT of Einstein. And since the space-time curvature gives the mass of the proton, and it is associated with the maximum of the radiation spectrum through a coefficient of 4,965, hence taking into account [5] we have:
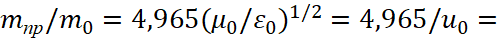
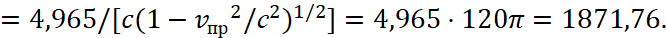(35)
Next, we must write:
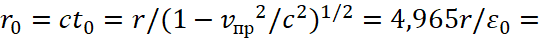
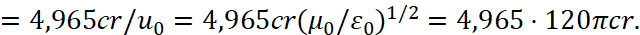(36)
Accordingly, we are substituting formula (29) in (34) we get:
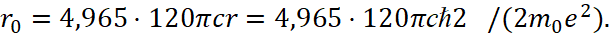(37)
Next, we take into account the constant of thin structure, which binds constants into SI measurement systems in the form:
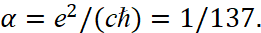(38)
Hence, for c=1/h, m0=1/c we have:
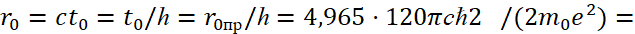(39)
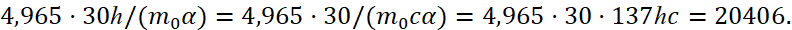In other words, we have received, regardless of the system of calculus, the value! This is connected to the fact that here it is necessary to take into account that the opposites are connected through the significance of exchange ‒ the speed of light, and the length and time in the opposites are being changed in the view. Therefore, instead of the magnitude r0 in one opposite, we have the ratio of opposites in the form of r0пр /h = t0 /h, that is, the time and length has replacing each other, and the quantitative count is from the minimum significance in the universe expressed in terms of Planck's constant. Earlier, in article [5] we showed a similar normalization when calculating the ratio of the mass of a proton to the mass of an electron. This amount is comparable to the ratio of the radius of the 1-st orbit of the hydrogen atom to the radius of the electron by (29). However, in our case, we did not neglect the condition of the environment. It should be noted that if we take into account that according to Dirac theory, based on the Einstein energy formula e = q = ±1, and for c = 1/h, m0 = 1/c we have:
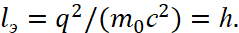(40)
That is, the electron has the smallest dimensions to frequency in wave form on the base of the formula ℏω=hf. It is clear that the electron radius characterizing the dynamics of the closed interaction will be rэ=ℏ. Accordingly, further division into smaller particles simply cannot be otherwise it is necessary to have another magnitude of the Planck constant. Actually, this transition to quantity, based on the smallest size equal to Planck's constant, solves the problem of "black holes" and eliminates the paradoxes associated with the violation of thermodynamic equilibrium and the Schwarzschild radius, and it will be shown later in next articles. However, we will continue the description of further fitting to the result made by Bohr. Actually, the fact that the coefficient equal to two is not taken into account in the formula (24) was being corrected by using a formula in which the internal energy of an atom is composed of the kinetic energy of an electron (the nucleus is stationary system in space of finding) and of the energy of interaction of the electron with the nucleus:
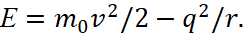(41)
It is clear that this formula is similar to the formula (12) according to which, due to the kinetic energy of photons E = hf, the electron overcomes the restraining forces of the crystal to obtain kinetic energy. However, there is no reason to talk about the internal energy of the atom. Accordingly, the magnitude of the kinetic energy of the electron is replaced by the potential energy of (23):
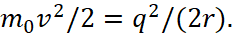(42)
The resulting value is substituted in (41):
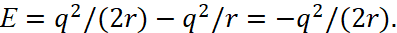(43)
Next, the calculated magnitude of r is used according to the formula (28), which is substituted into the formula (43):
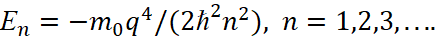(44)
When a hydrogen atom has the transition from the n condition to the m condition, a photon is emitted:
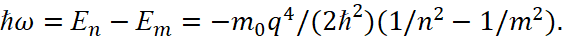(45)
The frequency of the emitted light is equal to:
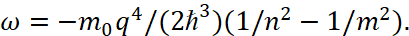(46)
At the same time, for the constant of Rydberg, the value was obtained:
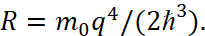(47)
Here by (45) for this Lyman’s series [13] n = 1, m = 2,3,4.... It can be seen that the maximum radiation energy at n=1 and m→∞ is determined by:
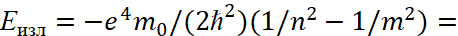
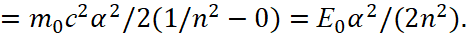(48)
Here E0 = m0c2.
In other words, this amount of energy corresponds to the radius of the orbit above which the electron can leave the hydrogen atom. Therefore, the maximum radiation is determined by the transition to the radius of the 1-st orbit of the hydrogen atom. It is clear that the occurrence of the constant of thin structure α in the formula (48) is determined by the chosen measurement system. Note that the paradox of the formula (48) is seen in the fact that it does not disclose how the influence of the environment is taken into account, since the multiplier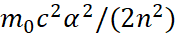 
is a constant. Further, the principle of substitution of the values of n and m has a probabilistic character. Hence, the appearance of various series of Lyman, Paschen, Brackett, Pfund finds only a miraculous explanation through an electromagnetic vacuum [14]. In other words, physicists were forced to use an interaction medium, but they called this medium an electromagnetic vacuum. But we will not rely on a "miracle" in the form of the sudden appearance/disappearance of particles in a vacuum, and we will show the derivation of formula (48) based on the law of inversely proportional relationship between opposites. Taking into account squaring of the formula (20), in order to get to the energy representation and taking into account formulas (38), we have:
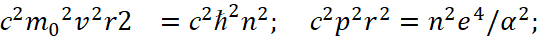
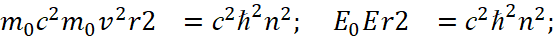
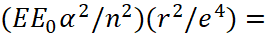(49)
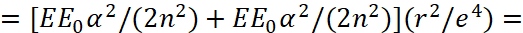
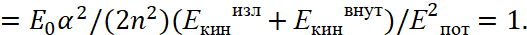
Here, we accept Eпот=e2/r, Eкинизл =(p)2/(2m0), Eкинвнут =(p)2/(2m0). In this case, we have an analogue of a harmonic oscillator. It can be seen that the magnitude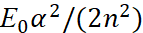 
in the formula (49) corresponds to the magnitude 
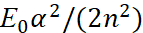in the formula (48). Then we can write:
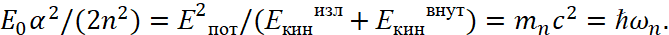(50)
It is clear that in this case we get the Rydberg’s constant. The formula (50) through the magnitude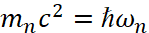 
allows us to take into account relativistic effects in accordance with SRT and GRT of Einstein in the form of an interaction medium as a space-time curvature, and here the density of the medium is determined by the constants of electric εε0 and magnetic μμ0 permeability, the relationship of which with the Lorentz transformations is determined by us in the formula [5]:
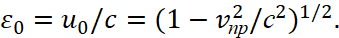(51)
Further, we take into account that the discretization of the environment is related to the Planck constant. Accordingly, we get:
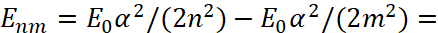
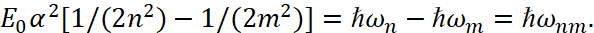(52)
Hence, the difference in spectral components, depending on the element in the periodic table, as well as the presence of different series of Lyman, Paschen, Bracket, Pfund, is determined in accordance with the implementation of thermodynamic equilibrium for certain orbits of electron rotation around the proton, which is associated with resonance at certain frequencies, based on the electrical and magnetic permeability of the medium. Thus, we take into account the parameters of the medium at discretization. It becomes clear that the equality of n and m corresponds to the equality of the orbits of rotation. At the same time, radiation is naturally excluded due to the transition from one orbit to other orbit. The magnitude in the formula (49) corresponds to the energy of the 1-st orbit of rotation of an electron around a proton in thermodynamic equilibrium. In other words, this energy of the particle is in accordance with the formula (25) without potential energy. In this case, we have the equivalent of the existence of a free particle with a closed exchange in thermodynamic equilibrium and conservation of energy in any coordinate system.
In contrast system in our theory, rectilinear motion becomes a closed orbital motion. In quantum mechanics, this magnitude Енуль=ℏω/2 is called zero energy of atom, which, according to physicists, is associated with an electromagnetic vacuum, which is a kind of reservoir from where virtual photons are "extracted" when they are emitted and where they "returned" when they are absorbed (for example, by an atom). Practically by assuming some kind of electromagnetic vacuum, physicists have confirmed the existence of a closed thermodynamic equilibrium with radiation and absorption. They were to present only one thing – to imagine the electromagnetic vacuum as a space-time curvature, thereby obtaining the presence of a common space-time continuum and electromagnetic continuum, but they could not do this last step from absent of knowledge of the process of replenishing the emitted energy by an electron at rotating around a proton.
We can see, the Bohr calculated the energy spectrum of atoms and orbits of rotation on the base of the classics of mechanical motion, at the same time he was forced to use the representation of kinetic energy in the form of potential energy, since otherwise it turned out that the greater the kinetic energy of the electron, the smaller the radius of the orbit. In other words, also before us, the Bohr actually introduced another system of mapping (observation) in which kinetic energy changes to potential energy. However, according to the laws of electrodynamics, the accelerated motion of an electron in orbit inevitably had to lead to electromagnetic radiation with loss of kinetic energy and with the falling of electron on the nucleus, but it was not observed in practice. Not knowing the mechanism of replenishing kinetic energy, the Bohr acted simply; he introduced the postulate about the prohibition of radiation of electron in discrete orbits. And then, in order to justify this postulation, probabilistic quantum mechanics arose, which led to a fitting to the result. However, our theory based on the relationship of the Lorentz force and the Coulomb force with the formation of a common electromagnetic and space-time continuum allows us to solve the problem of radiation and absorption without prohibiting the laws of electrodynamics.
Conclusions:
- When applying the formulas of classical mechanics, paradoxical solutions were used. Thus, according to formula (4), there was ambiguity in the value of radii at the same energy ratios. This would mean, for example, that the Earth can rotate around the Sun in two orbits.
- The resulting formula (20) follows not from the classical equation of the harmonic oscillator according to Bohr's idea, but from the formula of Louis de Broglie (23).
- The calculation of the radii of the Bohr orbits should take into account the condition of state of the environment, since otherwise the absence of interaction of objects with the environment means their complete independence, and then the objects are absent. The energy spectrum of radiation should also depend on the environment, since any interaction is carried out through the environment.
- The use of centrifugal force in a harmonic oscillator as a counteraction to the Coulomb force does not reveal the mechanism of energy conversion with a change in the direction of motion, since the action of centrifugal force is associated with the presence of energy conservation in the previous direction of motion. The mechanism of changing the direction is necessarily associated with the loss of components in the previous direction (radiation) and the getting of components of kinetic energy in the new direction. Otherwise, we must admit the existence of miracles without the existence of the laws of physics!
- When considering orbital motion, scientists allowed ambiguity in the use of centrifugal force. Thus, according to the formula (3), the centrifugal force compensates, for example, the Coulomb force (Fig. 2). At the same time, in the harmonic oscillator (10), centrifugal force is used as an attractive force that characterizes the potential energy (Fig. 7).
.png&w=640&q=75)
