В течение нескольких лет в курсе средней школы и в вузах появились разнообразные экономические задачи. До 10 класса в основном ученики решают задачи на движение, проценты, прогрессии, на тему «работа» и числовые зависимости. Перед школьниками встаёт цель - научиться понимать условия задачи, выявлять скрытую информацию, вникать в смысл каждого слова, предложения в ней, а также научиться связывать условия задачи с заданным вопросом.
В ходе решения задач №1, №11 первой части ЕГЭ, обычно применяют формулу для нахождения суммы на счете (a*(1+p)k), где k – количество лет, p – процентная ставка) [2].Перед нами появилась цель научиться решать задачи под №17 «ЕГЭ». Решать задачи можно несколькими способами. Я предлагаю способ решения таких задач. В ходе изучения работы брокеров, я решила дополнить, разнообразить и увеличить количество решений экономических задач.
Решение задачи №1
I. Табличный способ по акциям по истечении года
Алексей приобрёл ценную бумагу за 7 тыс. рублей. Цена бумаги каждый год возрастает на 2 тыс. рублей. В любой момент Алексей может продать бумагу и положить вырученные деньги на банковский счёт. Каждый год сумма на счёте будет увеличиваться на 10%. В течение, какого года после покупки Алексей должен продать ценную бумагу, чтобы через тридцать лет после покупки этой бумаги сумма на банковском счёте была наибольшей [1]?
Решение
Пусть Алексей продаст бумагу по истечении n-го года, то через тридцать лет после покупки сумма на его счете будет равна
an=(2n+7)•(1,1)30-n
по истечении n-го года. Значит, к концу n-го года (начало n+1 года) an+1=an+2(n+1-1)
an+1=an+2n=7+2n
Тогда, нам нужно найти номер максимального члена последовательности.
an= (2n+7)•(1,1)30-n, где n принимает целые значения от 1 до 30.
Выясним, при каких значениях n последовательность an возрастает, а при каких убывает. Для этого рассмотрим разность Dn=an-an-1, то есть доход в каждом месяце [3].
Найдем, an-1=(7+2(n-1)•1,130-(n-1)=(2n+5)•1,130-n•1,1(n>1)
Dn=(2n+7)•1,130-n-(2n+5)•1,130-n•1,1=1,130-n(2n+7-2,2n-5,5)=1,130-n•(1,5-0,2n)
Исследуем последовательность, т.к 1,130-n>0, а 1,5-0,2n≥0 при n≤7
Значит, при n=8 ,1,5-0,2n≤0;
Итак, Dn>0 при 1<n<7 и Dn<0 при n>8, следовательно, по истечении 7 лет нужно продать (т.е. в течении 8-го года) a0<a1<a2<…a7<a8>a9>an>…a15.
Ответ: В зависимости от вопроса «в течение какого года стоит продать?» – ответ: 8, если вопрос «По истечении какого года?», то ответ: 7.
Решение задачи № 2
Пенсионный фонд владеет ценными бумагами, которые стоят t² тыс. рублей в конце года t (t = 1; 2; ...). В конце любого года пенсионный фонд может продать ценные бумаги и положить деньги на счёт в банке, при этом в конце каждого следующего года сумма на счёте будет увеличивается на 25%. В конце какого года пенсионному фонду следует продать ценные бумаги, чтобы в конце двадцатого года сумма на счёте была наибольшей [5]?
I способ решения задачи №2
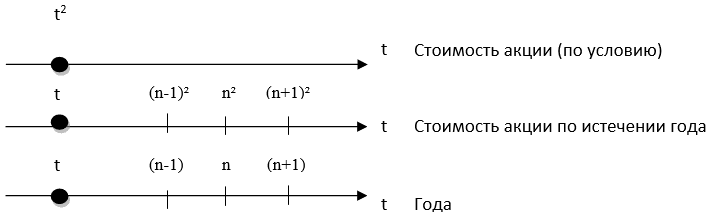
С помощью формул найдём дивиденд (надбавку) в ценных бумагах:
А) предыдущего года (до n-го года) – (n-1)²=n² - n² +2n-1=2n-1(дивиденд с (n-1) по n);
Б) последующего года (после n-го года) – (n+1)²-n²=n²+2n+1-n²=2n+1 (дивиденд с n по (n+1)).
С помощью формул найдём процент начисления (надбавку) в банковском счёте:
p=25% a(1+0.01p)=a(1+0.25)=1.25a.
А) предыдущего года (до n-го года) n²(1+0.25)=n²+0.25n².
Б) последующего года (после n-го года) (n-1)² (1+0.25)=(n-1)²+0.25(n-1)².
Сравним надбавки:
- с (n-1) по n год (надбавка в ценных бумагах должно быть меньше, чем в банковском счёте)
0,25n²>2n+1; n²>8n+4; n²-8n-4>0
D=64+16=80; n1=4+2√5; n2=4-2√5
- с n по (n+1) год (надбавка в ценных бумагах должно быть больше, чем в банковском счёте)
0.25(n-1)²<2n-1; (n-1) ²< 8n-4; n²-2n+1-8n+4<0; n²-10n+5<0
D=100-20=80; n1=5+2 √5; n2=5-2 √5
Таким образом, 4+2 √5<9 и 5+2 √5>10
поэтому наибольший член последовательности 9, то есть ценные бумаги надо продавать в конце девятого года. Ответ: 9.
II способ решения задачи №2
Пенсионный фонд владеет ценными бумагами, которые стоят t² тыс. рублей в конце года t (t = 1; 2; ...). В конце любого года пенсионный фонд может продать ценные бумаги и положить деньги на счёт в банке, при этом в конце каждого следующего года сумма на счёте будет увеличивается на 25%. В конце какого года пенсионному фонду следует продать ценные бумаги, чтобы в конце двадцатого года сумма на счёте была наибольшей [4]?
Решение
Если пенсионный фонд продаст ценные бумаги в конце года k, то в конце двадцатого года на его счёте будет: ак = k; 21,2520-k тыс. рублей.
Сравним числа ак и ак+1: ак+1-ак = (k+1)
Уравнение -0,25k ² +2k+1 = 0 имеет корни 4 (1 +- 1, 2 5).
Таким образом, ак+1>ак при k ≤ 8; ак +1 <ак при k ≥ 9.
Значит, а9> а8 > ... > а1 , а9 > а10 > ... > а20, поэтому наибольший член последовательности (ак) – это а9, то есть ценные бумаги надо продавать в конце девятого года.
Ответ: 9.

.png&w=640&q=75)