Алгоритм быстрого вычисления матрицы расстояний для решения задачи планирования множественных маршрутов

На современном этапе в условиях цифровизации всех сфер человеческой жизнедеятельности вопросы разработки, апробации, внедрения и оптимизации технологий приобретают особую актуальность и практическую ценность. С учетом высокой степени проникновения технологий в экономические процессы, важнейшей задачей становится оптимизация процессов планирования множественных маршрутов. Последние оказывают весомое влияние на состояние транспортной отрасли и проникают во все без исключения сферы хозяйственной деятельности – от непосредственно самой логистики, до перераспределения продовольственных товаров и доставки пациентов во время пандемии коронавируса. Применение современных технологий и алгоритмических решений для целей планирования маршрутов на транспорте основывается на использовании уникальных подходов, которые бы обеспечили высокий отклик и управляемость, выступили бы в качестве оптимальных решений на базе программных продуктов, нацеленных на построение маршрутов. При этом важно, чтобы программный продукт и алгоритм эффективно решал разнородные задачи, вне зависимости от сложности условий и дополнительных с точки зрения программы трудностей.

Актуальность разработки алгоритма быстрого вычисления матрицы расстояний для решения задачи планирования множественных маршрутов обусловлена и тем, что подобные алгоритмы могут быть повсеместно применены в различных сферах промышленности. Сегодня существует достаточно обширная система различных методов планирования маршрутов, при этом, в процессе выбора одного из них, возникает задача по сравнению возможностей и недостатков, поиску компромиссов и условий оптимизации каждого из алгоритмов в целях эффективного нахождения оптимального маршрута. Более того, в ряде сценариев отдельные алгоритмы могут демонстрировать снижение эффективности, что требует упрощения или видоизменения подхода к построению маршрутов. Одной из подобных задач становится быстрое вычисление матрицы расстояний для планирования множественных маршрутов.

Цель исследования – разработать и описать алгоритм быстрого вычисления матрицы расстояний для решения задачи планирования множественных маршрутов.

Вопросы планирования маршрутов приобретают все большую практическую ценность и научно-исследовательскую значимость с ходом процессов цифровой трансформации. Исследование вопросов вычисления и построения оптимальных маршрутов пользуется высоким спросом в научных кругах, о чем свидетельствует положительная динамика публикаций. Ряд авторов успешно решают задачи оптимизации маршрутов и вычисление маршрутов на дорожном графе. Например, в работе А.М. Валуева раскрываются возможности оптимизации задач по вычислению наиболее коротких маршрутов в сети в целях рационального распределения грузовых перевозок. Исследование автора демонстрирует практическую ценность работ, посвященных построению оптимальных маршрутов на дорожном графе [2]. В.П. Степанова и П.В. Степанов также решают задачи построения оптимальных маршрутов, фокусируясь на формировании планов проезда между предприятиями связи. В исследовании авторов достаточно четко раскрываются возможности применения алгоритма Дейкстры для решения задач построения оптимальных маршрутов между заданными точками. Идея оптимизации состоит в сочетании алгоритма Дейкстры с авторской математической моделью – это позволяет рассчитать граф, состоящий из девяти вершин и двадцати ребер [7].

Однако в условиях современных логистических компаний, в особенности при построении маршрутов дальнего следования, применение сугубо алгоритма Дейкстры показывает неэффективность, поскольку требует оптимизации с точки зрения скорости вычисления множества операций и выдачи оптимального маршрута на большом дорожном графе. На проблемы вычисления больших матриц указывают и О.А. Плотников и Е.С. Подвальный – авторы исследования, фокусируясь на задаче поиска оптимального маршрута между двумя точками с нерегулируемым весом ребер, выделяют высокое значение проблемы оптимизации разрабатываемых алгоритмов с точки зрения скорости выдачи готового решения. Первично составленный алгоритм авторов демонстрировал скорость в 2876 мс., которые требуются для просчета трудного случая. В качестве способа оптимизации авторы предлагают оптимизировать непосредственно сами дорожные графы в целях сокращения времени работы алгоритма. Решением в оптимизации стало ориентация на принцип LIFO, который отражает использование структурированных данных из вершины списка. Как итог, за счет LIFO, авторам удалось увеличить скорость работы алгоритма на 7% и 15,6% для легких и трудных задач соответственно [6].

Д.А. Барыбин и соавторы, сравнивая алгоритм Дейкстры с алгоритмом Беллмана-Форда в рамках решения задачи поиска наиболее оптимального с точки зрения расстояния пути, отмечают, что в рамках смоделированной задачи алгоритм Беллмана-Форда демонстрирует большую скорость [1]. Вместе с тем, стоит заметить, что для решения сложных задач описанный алгоритм не может быть использован ввиду того, что он демонстрирует значительное сокращение эффективности при построении больших матриц, в которых именно алгоритм Дейкстры (в различных его представлениях и модификациях), зачастую, задействуется в реальной практике.

Эффективность использования алгоритма Дейкстры для целей построения оптимальных маршрутов демонстрируется в работах М.Д. Копылова, К.А. Хохлова [4], И.Н. Ищука, М.А. Лихачева [3], А.В. Пановой [5]. Авторы научных статей схожи во мнении о том, что алгоритм Дейкстры наиболее оптимален для решения сложных (больших) задач, при построении матриц маршрутов. Тем не менее, в работах также прослеживается мнение о том, что сегодня существует потребность в решении задач оптимизации скорости работы подобных алгоритмов, внесение персональных коррективов и поиск решений, способствующих оптимизации больших задач.

Таким образом, проведенный краткий литературный обзор показывает высокую актуальность и практическую ценность задачи по планированию маршрутов на транспорте. При этом, выявлено существенное ограничение многих из существующих методов, которое проявляется в высоких ресурсно-вычислительных и, соответственно, временных затратах на организацию вычисления операций. В том случае, если в систему случайным образом закладываются ошибки (при вводе первичных данных), формируются повышенные риски нарушения планирования и организации транспорта, что требует выработки соответствующих решений. Обусловлено это тем, что скорость просчета матрицы всех маршрутов остается достаточно низкой, в особенности если алгоритм не оптимизирован под объемные задачи. В свою очередь все это приводи к временным потерям, которые могут негативно сказаться на состоянии планирования транспорта.

На наш взгляд, решением проблемы скорости построения (планирования) маршрутов на транспорте может стать разработка авторского алгоритма быстрого вычисления матрицы расстояний для решения задачи планирования множественных маршрутов.

В рамках оптимизационных процессов поиск наиболее оптимального из существующих вариантов маршрутов становится, фактически, классической задачей, для решения которой требуется набор необходимых входных данных. В частности, требуется установление необходимого расстояния между точками, времени их прохождения, что закладывается в основу формирования соответствующих матриц расстояний и времен.

Построение подобных матриц, в особенности при организации множества параллельных запросов и на дальние расстояния, требует высоких ресурсных (вычислительных) мощностей и осуществления широкого числа типовых операций, что делает невозможным быстрое построение маршрутов. По нашим подсчетам, на просчет матрицы расстояний требуется свыше десяти минут; при этом, если рассматривать большую размерность матрицы, на решение описанной задачи уходят часы.

В целях оптимизации логистики, например, по пяти тысячам кратчайших маршрутов (из точки «А» в точку «Б»), сложенных в одну единую поездку, требуется построение двух матриц чисел размерностью пять на пять тысяч каждая. При этом, задача усложняется ввиду того, что в разные временные интервалы интенсивность передвижения изменяется. С точки зрения временного распределения маршрутов наиболее значимым становится точный и комплексный просчет времени, в период которого наблюдается повышенная активность на дороге (пробки). Для оптимального решения описанной задачи выбрано тринадцать часовых срезов в объемах пять на пять тысяч каждый. Как итог, суммарное исчисление подобного числа маршрутов с учетом временного фактора составляет 325 млн. маршрутов с учетом реального состояния дорожного движения.

Решение задачи построения кратчайшего (принятого за наиболее оптимальный) маршрута основано на алгоритме Дейкстры, который представлен в виде дерева кратчайших путей в зависимости от точек и узлов между ними [8]. Упрощенно задача алгоритма может быть представлена в виде круга, центральной точкой которого является «старт», а точкой на оси круга «финиш» (рис. 1).

Рис. 1. Построение площади маршрута на примере круга

В целях оптимизации представленного на рис. 1 алгоритма требуется построение двух кругов с общей точкой пересечения. При этом центром каждого из кругов становится точка «А» и точка «Б» (рис. 2):

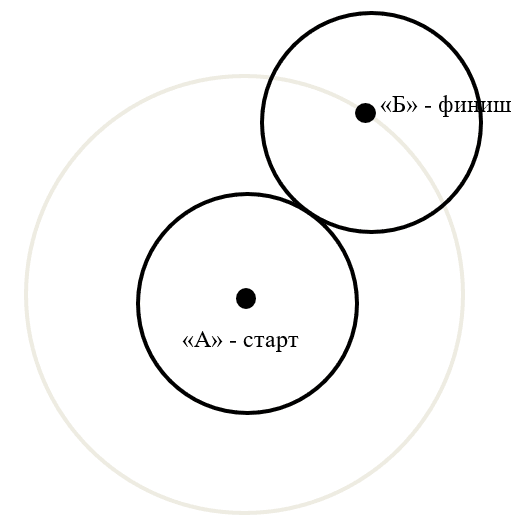
Рис. 2. Реализация алгоритма Дейкстры на примере круга

И хотя представленный на рисунке 2 способ оптимизации построения маршрута является условным, а реальный рельеф дорожного полотна достаточно структурированным, это позволяет более эффективно выстраивать маршруты при условном переборе одной улицы к другой, пока не будет составлен оптимизированный маршрут. Уже на данном этапе видно, насколько обширным может быть число необходимых для построения оптимального маршрута вычислений; причем это обширное число может быть значительно увеличено ввиду необходимости построения дополнительных уровней иерархии, что в конечном счете негативно скажется на работе алгоритма и скорости поиска оптимального маршрута на транспорте. Однако даже алгоритм Дейкстры не способен покрыть решение описанной задачи с просчетом больших матриц.

Для целей оптимизации требуется построение ряда в матрице, который исчисляется в виде расстояния каждой взятой точки для всех оставшихся. Это позволяет параллелизировать вычисления за счет одновременного измерения расстояния как до дальней, так и до близких точек. На рис. 3 продемонстрирован наглядный пример матрицы точек:

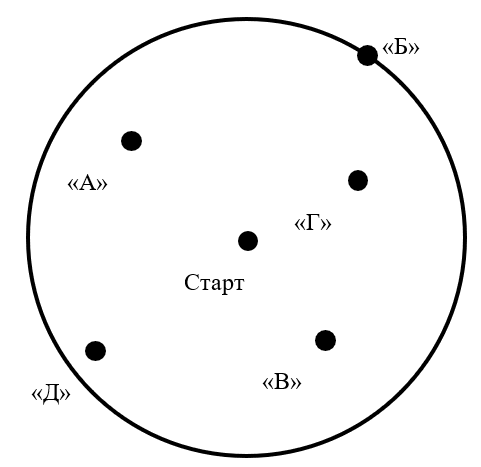
Рис. 3. Точки маршрута, по которым вычисляется расстояние

Обращаясь к рисунку 3, заметим, что самым дальним расстоянием от точки до точки является расстояние до точки «Б» — это самая удаленная точки во всем маршруте, которая располагается на границе площади вычислений. Пока осуществляется просчет маршрута до этой точки, параллельно реализуется задача по просчету более коротких маршрутов, т.к. в любом случае следуя дальней точке, придется считать более ближние.

Учитывая поставленное условие, согласно которому необходимо вычислить пять тысяч маршрутов, с условной скоростью построения одного в 10 миллисекунд, время вычисления по описанному алгоритму составит около 50 секунд, что демонстрируется линейным графиком матрицы расстояний (рис. 4):

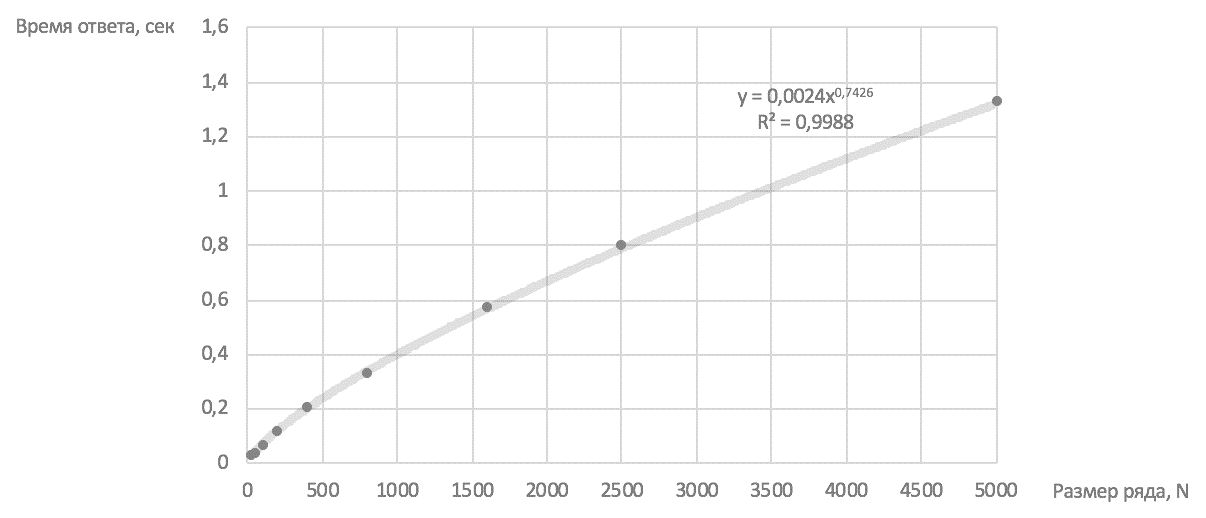
Рис. 4. Время вычисления строки в матрице для разных маршрутов

Обращаясь к рис. 4, заметим, что одна строка в пять тысяч маршрутов выстраивается за 1,3 секунд; при этом, время вычислений согласно графику тренда увеличивается несколько медленнее, чем это происходит при линейном построении. В таком случае значение матрицы расстояний составляет 0,74, что позволяет осуществлять просчет представленных 325 млн. маршрутов. Время на просчет данных маршрутов составит 84,5 тыс. секунд, что в часовом эквиваленте составляет 23,47 часа.

Однако, за счет параллелизации алгоритма (не линейного, а параллельного просчета), при следовании к дальней точке и просчете сопутствующих коротких расстояний возможно увеличение скорости при предоставлении необходимых мощностей. При применении 50 CPU (вместо 1, как в первом случае) все вычисления осуществляются примерно за 0,5 часа (рис. 5):

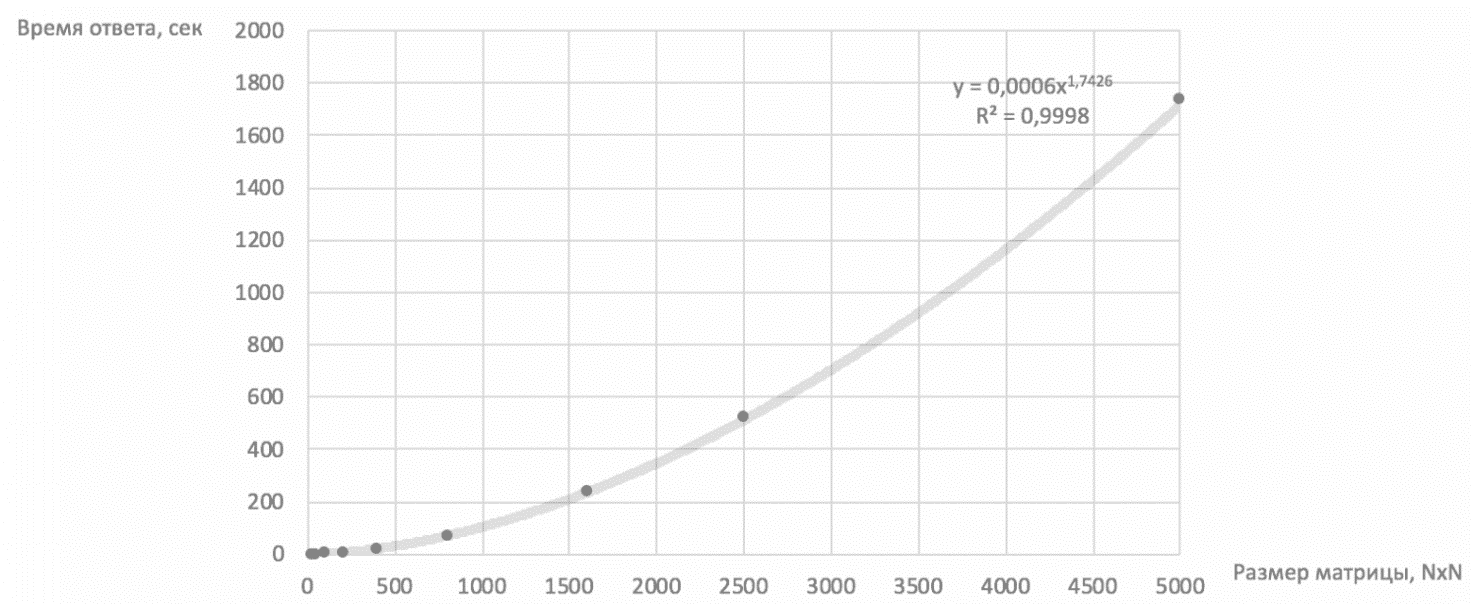
Рис. 5. Время вычисления 325 млн. маршрутов при оптимизации за счет параллелизации

Обращаясь к рис. 5, заметим, что на графике представлено время вычисления тринадцати матиц в размерности N*N при их перераспределении по рядам на 50 CPU (разделение на пятьдесят вычислительных параллельных процессов).

Однако даже такого алгоритма становится недостаточно для просчета огромного числа точек. В случае, если количество маршрутов увеличится до 10 тыс., то придется увеличивать вычислительные мощности, или значительно возрастет время просчета. Такой алгоритм не позволяет быстро просчитать необходимые маршруты, а при ошибочном вводе данных не позволяет осуществлять мгновенный пересчет.

Для целей оптимизации возможным решением становится построение алгоритма с линейной сложностью, в котором время становится линейной категорией (рис. 6):

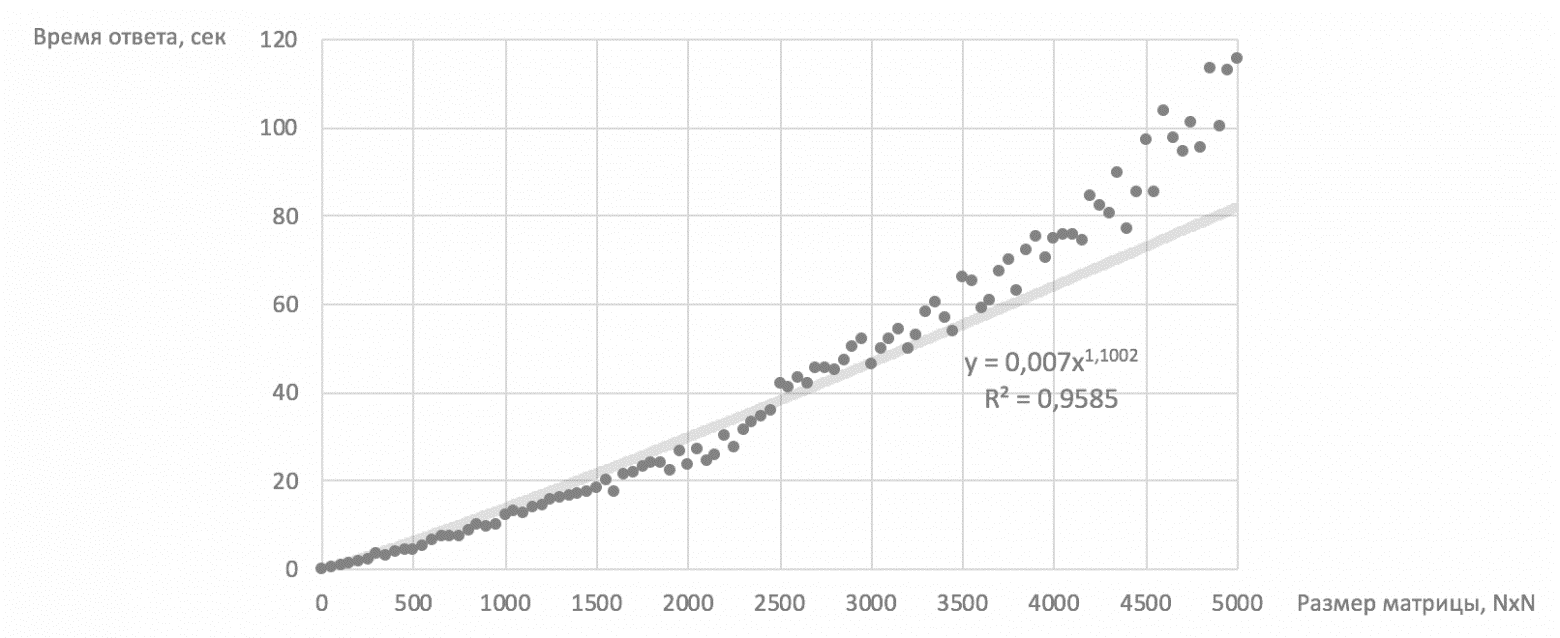
Рис. 6. Алгоритм быстрого вычисления матрицы расстояний для решения задачи планирования множественных маршрутов

За основу реализации алгоритма, представленного на рисунке 6, взята мощность 1 CPU. В таком случае на одну матрицу размером пять на пять тысяч маршрутов затрачивается 115 секунд (для поиска оптимального маршрута). Авторский алгоритм состоит из двух перспективных решений (рис. 7):

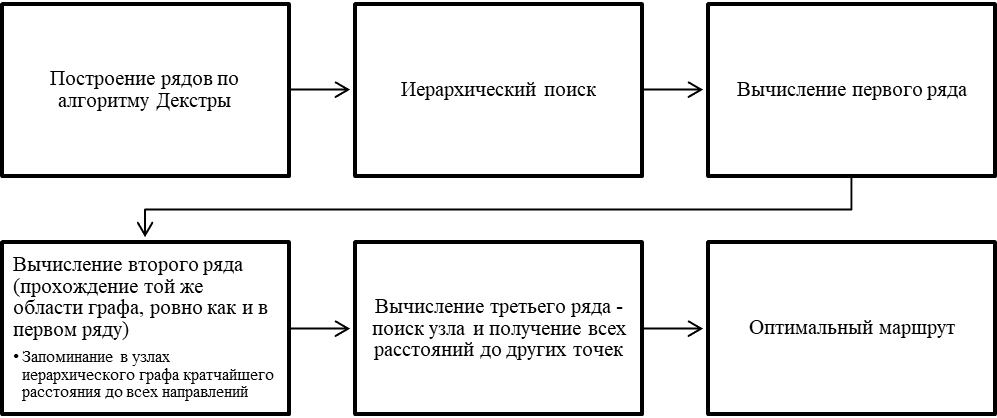
Рис. 7. Авторский алгоритм быстрого вычисления матрицы расстояний для решения задачи планирования множественных маршрутов (принципы работы)

Рисунок 7 наглядно показывает, что представленная система сочетания алгоритма Дейкстры и иерархического поиска рядов с запоминанием кратчайших расстояний до всех направлений позволяет выстраивать оптимальные логистические маршруты, снизить потребление аппаратных мощностей и при этом сократить время обработки запросов. Подобная система выстраивает около 200 тыс. маршрутов в секунду на одно вычислительное ядро, что является, определённо, весомым результатом.

Таким образом, результаты проведенной разработки алгоритма быстрого вычисления матрицы расстояний для решения задачи планирования множественных маршрутов демонстрирует высокие перспективы расчетов с высоким скоростным откликом. Идея алгоритма основана на сочетании алгоритма Дейкстры и иерархического поиска рядов с запоминанием кратчайших расстояний до всех направлений, что может применяться при построении оптимальных транспортных маршрутов при множестве точек.