The essence of considering the curvature of the path of passage by electromagnetic components in environmental space at the speed of light follows from the fact that otherwise, with the annihilation of particles such as an electron and a positron, it would be impossible to explain the transition from corpuscular particles to photons moving at the speed of light. It would be necessary to come up with a way to transform corpuscular particles into photons, which is not associated with miracles. During the transition of electromagnetic components from rectilinear motion to closed motion, and vice versa, the speed of light is being preserved, while the particle-wave dualism is being preserved too, and the transition itself does not look miraculous, since the physics of the transition is only a change in the direction of motion during the interaction of the simplest objects of the universe, which are electronic and muonic neutrinos (antineutrinos). It is clear that at the same time it is necessary to understand how and from which idea the change of direction of movement occurs in compliance with the condition of constancy in the speed of light. Why this is important follows from the fact that the principle of changing the direction of motion of an electromagnetic wave over the shortest distance has been considered in geometric optics, and it is based on a change in direction according to the Fermat principle [1]. This principle states that a ray between two points is a curve connecting these points, and along a curve the optical path length is minimal. In this case, the length of the optical path is calculated by the formula:
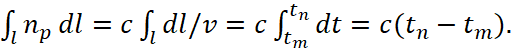(1)
Here np=c/v, tn‒tm is the propagation time with velocity v (x, y, z) along the path l from point min to point n. It turns out that in a vacuum, this propagation must be rectilinear, but the curvature is associated only with in homogeneity in the medium, which gives propagation at a speed below the speed of light. However, in practice it is known that the curvature of the motion of light, depending on the space-time conditions of the medium (gravitation), occurs and at the same time the movement of light cannot slow down, as then we would have elementary particles moving at a speed less than the speed of light, and their velocity would have to drop to zero. In addition, the movement of objects at a speed below the speed of light is unambiguously interpreted by SRT of Einstein through the presence of a mass of rest obeying the formula E = c (P2 + M02c2)1/2, and not the formula E = mc2, without a rest mass (M0) and the presence of charged particles (here, we have connection of magnitudes of charged particles with absorption and radiation).
When leaving such an optically dense medium through propagation of light, the question would be how these particle-wave objects regained a speed equal to the speed of light. In addition, the energy of the electromagnetic wave has increasing in frequency when approaching the center of gravitation, and the wave has decreasing in frequency when moving away from the center of gravitation. That is, in the Fermat scheme, the very principle of interaction of an electromagnetic wave with a space-time curvature is omitted. And the essence of the principle should be that a change in the direction of movement means the appearance of electromagnetic components in those directions in which they did not exist before, and the disappearance of the previous directions of movement of the electromagnetic wave. That is, we have the result of the mutual transformation of electromagnetic components in medium of space-time curvature, according to the principle of transition from a rectilinear moving to a closed one, and vice versa. This option of moving does not fit into the usual Maxwell equations, because for this it is necessary to have the transformation of time and length into electromagnetic components, and vice versa. To this problem of the connection of electromagnetic and so-called gravitational forces the A. Einstein has devoted his latest 30 years, but has not been able to solve this problem. 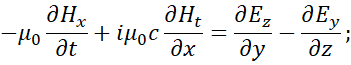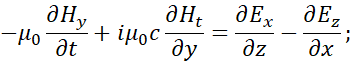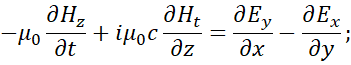However, we managed to get this solution on the base of improved equations of Maxwell 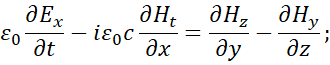[2]:
(2)
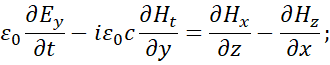
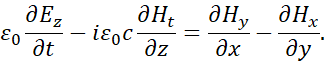
Having received the sources of radiation and absorption in the form of projections along time of electromagnetic components, we can now solve the problem of the curvature of light in the gravitational field (space-time curvature), as there is a connection. The actual representations in (2) allow solving electrodynamics’ problems based on the Huygens-Fresnel principle, taking into account all parameters of the medium. The form of equations (2) is based on the representation of Maxwell's equations with fictitious (imaginary) currents to describe the Huygens-Fresnel principle, but taking into account of presence of fictitious currents by physical essence with mapping through electromagnetic components by their projections onto time, and taking into account the corpuscular-wave properties with the introduction of an imaginary unit i = (‒1)1/2, and it allowed to combine the corpuscular and wave properties in one object. 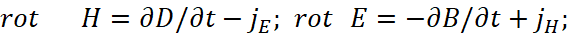This result comparing can be seen from the well-known equations 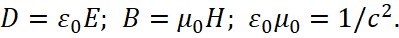[3]:
(3)
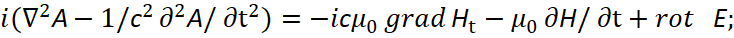
In this case, with improved Maxwell equations based on classical transformations in electrodynamics with substitution of some equations into others with changes that are expressed through the using of the mathematical operation of the rotor (rot), we can obtain wave processes with sources of radiation (of absorption), according to the formulas 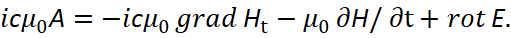[4]:
(4)
Here A is a vector-potential. Equations (4) characterize the well-known Helmholtz equation with a source of radiation (absorption) through fictitious currents in classical electrodynamics [5], but taking into account the particle-wave properties. It is clear that all transformations associated with a change in the direction of motion of the wave as a particle-wave object are associated with interaction with the medium, that is, space-time curvature, which is displayed through radiation and absorption. Otherwise, there is no interaction and the electromagnetic wave must move independently and rectilinearly.
However, we will analyze the solutions obtained earlier in electrodynamics on the basis of the interaction of an electromagnetic wave with an optically dense medium and find out why they are paradoxical for a vacuum. The actual initial analysis of refraction in environment is based on the consideration of boundary conditions [6].
The essence of constructing solutions in classical electrodynamics is based on the imposition of boundary conditions, or, how scientists say, on the "stitching" of the solutions on the boundary of the regions. In fact, the stitching means that there is a transformation of something into something other, otherwise it is impossible to fix any changes, but in this case the logic of this transformation itself is important, obeying the laws of physics without paradoxes. For electric induction and electric intensity of field, the initial equations associated with the charged particle are used in the form:
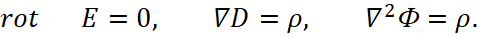(5)
In this case, the actual real electric density of charged particle is considered instead of fictitious charged particle, as, for example, in the Poisson equation, which follows from the Dalembert wave equation under the assumption that the changing of components into time is zero:
∇2Ф‒1/с2∂2Ф/∂t2= ‒ρ/ε0. (6)
Here Ф is a vector-potential. In other words, with this approach, we moved away from the dynamics of the interaction of electric and magnetic fields and began to use field strengths as a result of the formation of corpuscular objects based on a certain real charged particle. This is exactly what the second equation in (5) says, according to which electric induction is not the result of a change in the magnetic field along time and space, but the result of the presence of a static charge associated with a corpuscular object. The essence of the error here is that the presence of an electric field is not considered as a result of the dynamics of exchange through the speed of light between opposites by the simplest objects such as electronic and muonic neutrinos (antineutrinos), but here is being assumed the existence of a certain separate electric field associated with a real charged particle, with its field propagation to infinity regardless of its connection with the opposite charged particle. In this case, the directional movement from one charged particle to another charged particle, which is associated with the gradient (grad), is replaced by divergence (div). As we will see below, this gives a paradox at using so-called surface charges. It is clear that the paradox here is also in the duality of the formation of electrical induction, and this is precisely the adjusting for the result, and it we will show later.
In electrodynamics, it is believed that the "stitching" conditions which are being imposed on the vectors E, D, B, H on the base of deriving boundary conditions are easy to deduce through using the integral form of Maxwell's equations.
That is, in this case, the integral form of calculating the charge of particle is taken according to the Ostrogradsky‒Gauss theorem on the base of the second equation (6). At the same time, instead of sum from electric induction according to the theorem, subtraction was applied, and the formula was used:
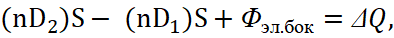(7)
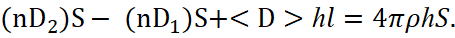
From the formula (7) it can be seen that with the height h tending to zero, the magnitudes of the equation with <D> and ρ should tend to zero too. At the same time, contrary to mathematics, the significance of the charged particle is transformed into the concept of a surface charge ξ, and in practice does not equal zero, but the significance of <D> is assumed to be zero. Hence the formula is being obtained:
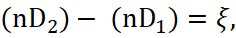(8)
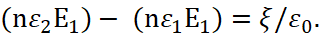
Here n is a unit vector. However, according to Fig. 1 it can be seen that if we proceed from the presence of a charged particle and here we have electric field magnitude which is equal in all directions (otherwise we will not get divergence), then we will get zero instead of superficial charge.
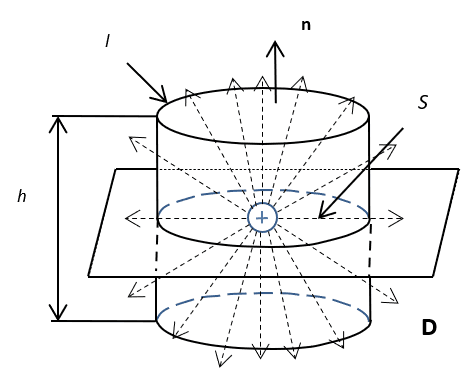
Fig. 1
Hence, we have conclusion is that this approach has an explicit adjusting for the result, and it gives the paradox in which the charged particle must have an uneven distribution. From here, for excluding of paradox, a gradient is needed instead of a divergence from the electric field, with the intersection of the electric field strength of the boundary of the environment, with magnitudes of electrical permeability ε1 and ε2 along normal vector.
It is clear that the question here is what has become fact of the difference between the vectors of electrical induction on the boundary of the division of environment, as the absence of change would mean the absence of interaction. A static surface charged particles with the presence of divergence is not suitable for these purposes, since a gradient is needed that gives a change along direction of action only. It would be possible to assume the transition at changes from electric induction to the magnetic component immediately on the base of usual Maxwell's equations, but this means independence from the medium of passage, and it actually followed from the usual Maxwell equations with the absence of static and fictitious charged particles according to formulas:
rotE = ‒∂B/∂t, D = ε0E, divЕ = 0 (9)
с2rotВ = ∂Е/∂t, B = μ0H, ε0 μ0 = 1/с2, divВ = 0. (10)
The absence of fictitious charges and currents led to the absence of a wave bending around an obstacle with a change in the direction of action according to the Huygens-Fresnel principle, which means the absence of interaction with medium through exchange. Thus, the change in the normal component of the electric field to the boundary of the division of environment can only be associated with a fictitious charges, which in our theory in the improved Maxwell equations are associated with the projection of the electric field onto time and in the equation have the significance of needed gradient. In (8), the normal component of electrical induction to the boundary of division of environment is considered, but there is also a tangential component, and here, by the way, another condition is chosen for the formation of an electric field not based at a surface electric charge, but based on Faraday's law on integral form:
(11)
At the same time, we have:
(12)
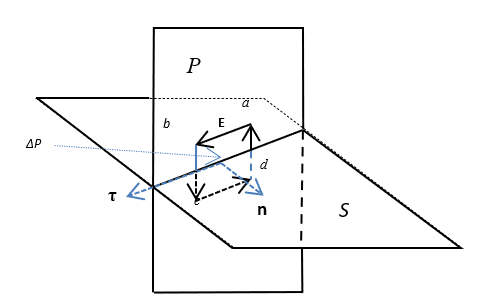
The integration along the contour L of the electric field strength (Fig. 2) is performed here on the sides ab, bc, cd, and da. At the same time, we have ab=cd=Δl, bc=da=Δh. The calculation of the magnetic flux in the right part of equation (11) is performed through the area ΔP, which is being bounded by the contour L. Accordingly, we are getting result:
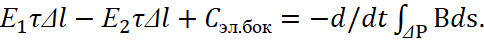(13)
In the limit at Δh→0, the sides ab and cd of the contour L coincide at the boundary; at the same time, ΔP→0. As a result, the magnitude Сэл.бок and the right side of the equation associated with the induction of the magnetic field (13) disappear.
At the same time, we see an obvious paradox associated with the fact that if we take into account Faraday's law, the presence of an electric field is directly related to a change of the magnetic field, but here it turns out that there is no magnetic field and its changes during of time, but there is an electric field and the boundary condition has the form:
(Е1-Е2)τ=0. (14)
Accordingly, we have not knowledge how the electric field of an electromagnetic wave can exist without the changing of the magnetic component, since the another variant is due to the presence of a static charge, but then there must be a so-called surface charge (8) with the paradox of charge in homogeneity in environment.
At the same time, how the direction of the electric component of the wave is being changed to the opposite direction on boundary of division of the environment, as can be seen in Fig. 2, also remains a mystery. In other words, this conclusion (14) also has no evidentiary basis and in fact we have the two postulations (8) and (14) for normal electric components and for tangential electric components.
A similar conclusion was made for magnetic components. In this case, to determine the significance of the vector n, the integral equation (12) was used, which gave the equality:
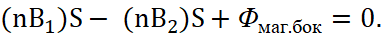(15)
In the limit at magnitude Δh→0, the magnetic flux through the lateral surface tends to zero Фмаг.бок→0. From here we have:
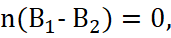(16)
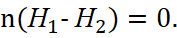
Here we also have a paradox in which a closed magnetic field exists separately from a changing electric field, in fact, there is no interaction of opposites and, accordingly, wave-particle dualism. At the same time, crossing the boundary of division of environment by magnetic induction does not lead to a change in the magnetic field, and it actually indicates the independence of the magnetic field from the propagation medium, and this is also a paradox, because, for example, the presence of a magnetic core in the view of a medium at the boundary of division affects the direction of vector of magnetic induction. The tangential component of the magnetic field is based on the use of another integral Maxwell's equation:
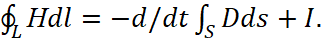(17)
In this case, this equation is transformed to the form:
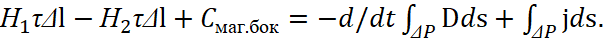(18)
Here the magnitude Смаг.бок is contribution of the lateral sections of the contour is disappearing at value Δh→0, at the same time the first of the integrals into the right part of the equality is disappearing too. The second integral expressing the common conduction current passing through ΔP is not disappearing, at magnitude Δh→0, and we have a surface current η. As a result, the general formula will be presented as an expression:
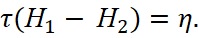(19)
Thus, the dependence in which an alternating electric field induces an alternating magnetic field is removed again and the dependence on a moving surface charge is left. However, it is known, that at a point in space and time outside the object which is representing the surface charge, there is precisely an electric field that changes when the charge moves. And it is this changing electric field that causes the appearance of a magnetic field. That is, the presence of a magnetic closed field in the tangential component is not associated with the intersection of the boundary of the medium, but with varying electric field along time, as there is nothing else at this point in space and time. In other words, the real factor in the formation of a magnetic field is the varying electric field along time. Accordingly, this equation (19) is used both in the Bio–Savard’s law and without boundary of medium. Accordingly, we have the question: "How then be at showing the change in the magnetic field at the boundary of division of the medium in reality?" In this case in reality, to solve the problem of changing the magnetic field at the boundary of division of the mediums, it is necessary to use the fictive magnetic charges associated with the projection of the magnetic field along time and the presence of a gradient in the direction of the vector. Thus, the assumptions made in the derivation of boundary conditions in classical electrodynamics are obviously have the mistakes, due to the fact that truncated solutions are used that do not correspond even to elementary objects of the universe based on electronic and muonic neutrinos (antineutrinos), which characterize the objects of the universe in two opposites.
Next, physicists decided to combine paradoxical boundary conditions with Fermat's principle, which is also not devoid of paradoxes, and in order to understand the errors of this step, let's use a closer look at the reflection and refraction of electromagnetic waves at the flat boundary of division of two mediums (Fig. 3).
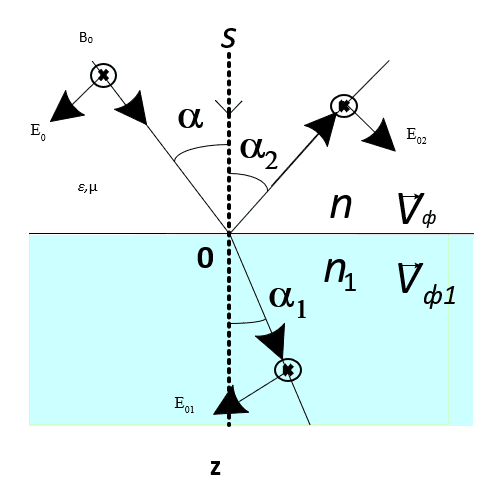
Fig. 3
According to Fig. 3, we have the propagation of electromagnetic waves in a space filled with two homogeneous mediums separated by a flat surface z = 0 and characterized by constants of permeability ε,μ (z > 0), ε1,μ1 (z < 0). The velocity of propagation of electromagnetic waves in each medium is equal, respectively [7]:
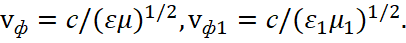(20)
In the simplest private case, in the presence of a flat boundary of division z = 0, the electromagnetic field is described by three monochromatic flat waves, in the region z > 0 there is a transmitting E, B (wave vector k) and a reflected E2, B2 (wave vector k2), and in the region z < 0 there is a refracted wave E1, B1 (wave vector k1). The wave falling on the boundary of division of the mediums is being considered linearly polarized, that is, it can be represented as:
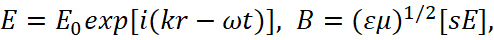
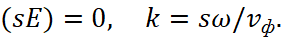(21)
Here, s is the unit vector of the normal direction. At the same time, the boundary conditions must be satisfied at the boundary z = 0 in accordance with (8), (14), (16) and (19), and at presence of the normal vector s. And then the fitting to the result is visible in the fact that it is assumed that there are no free surface currents and charges, on which the conclusion of the boundary conditions itself was built, with a change in the parameters of the electromagnetic wave. In classical electrodynamics [7], when surface currents and charges are replaced by electric field strength and magnetic field strength, the equations take the form:
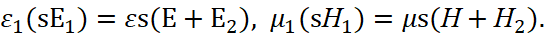(22)
Here, the first equation has accordance to the normal component of the electric field vector to the boundary of division of the mediums, and the second equation has accordance to the normal component of the magnetic field strength to the boundary of the mediums. Similarly, we have a result for the second pair based on boundary conditions for tangential components:
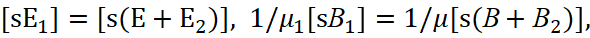
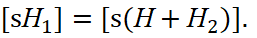(23)
In fact, we see that in the first equation (22), the amount of the surface charge is replaced by the amount of the electric induction of the reflected electric field of the electromagnetic wave. It is clear that in this case, we do not know how the transformation occurred at the boundary of division of the mediums, with the getting of a reflected wave, but we proceed from practice. We have a similar result for the magnetic component. It should be noted that in (22) and in (23) in classical electrodynamics, the change in the electric and magnetic fields at the passing the boundary of division of mediums without the so-called surface currents and charges looks the same. When deriving boundary conditions taking into account surface currents and charges in (8), (14), (16) and (19) the electric and magnetic components are being differed depending on their belonging to the normal and tangential components. And this was due to the presence of an intersection of the boundary of division of mediums with a change in the electric field strength from the surface charge (normal component) and of the magnetic strength formed by the surface current (tangential component). In the case of (22) and (23), instead of surface currents and charges, a reflected wave is introduced from the boundary of division of mediums with the presence of tangential and normal components without the physics of occurrence. At the same time, the conditions for the formation of changes for the intensity of magnetic fields have also been changed. Here, a transition was made to the same conditions at the boundary of division of the mediums for electric and magnetic components. And this is due to the fact that otherwise there will be a separation of electromagnetic components according to the unequal conditions of reflection and refraction for electric and magnetic components, and it contradicts the propagation of the electromagnetic wave in the common whole representation. Accordingly, the change in the interaction for an electromagnetic wave is associated with the intersection of the boundary of division of the mediums along the normal vector, and this is reflected in the form of coefficients from the magnitudes of electric and magnetic permeability. In the absence of crossing the boundary of the mediums, which is associated with the tangential component, there are also no changes from the interaction, but there is a result from the interaction in the form of a reflected wave. The reasons for formation of a reflected wave on the base of the presence of surface moving of charged particles and of charged particles have no explanation. More over, the electric and magnetic components of the reflected wave according to equations (22) and (23) turn out the independent significances, and are determined by the magnitudes of electric and magnetic permeability, but according to the principle of induction guidance by electromagnetic components through each other, this should not be. In this case, it turns out that the ratio of the amplitude proportions between the components of the electric and magnetic intensity of the reflected wave does not correspond to the proportion of the amplitudes of the components of the electric and magnetic intensity of the falling wave due to the differences between ε,μ (z > 0), ε1,μ1 (z < 0). When obeying Maxwell's equations and at propagation in the same medium, the proportions between the electric and magnetic components should be the same, the difference concerns only the energy of the falling waves and reflected waves. In addition, in the case of standing electromagnetic waves, the conditions are considered precisely according to the formulas (8), (14), (16) and (19), and this means that the fitting to the result at the boundary of division of the mediums is carried out depending on the conditions of further propagation, which does not correspond to the correct theoretical interpretation of the phenomena in the physics of the process, because there can be no ambiguity. This suggests that the environment cannot be considered outside of the processes of interaction, which has place in itself, and the environment determines the very principle of interaction.
It is clear that the form of equations (22) and (23) has a dependence of the presence of field strengths from the spatial location before the point of refraction (section) and after, since otherwise the law of conservation of quantity will not be observed. Since the principle of formation of reflected wave was not clear, and the interpretation of (22) and (23) gives paradoxes, a method similar to Fermat's principle was proposed taking into account the reflected wave. In fact, this is the law of conservation of quantity at the point of separation, which can be fulfilled in the presence of vectors containing phase multipliers of the type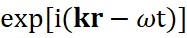 
at cause only if all phases coincide, which means there are no discontinuities. Hence, for any vector r lying in the surface of the partition, that is, at satisfying the significance (sr) = z = 0, the conditions must be executed:
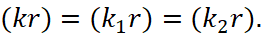(24)
It is clear that when an electromagnetic wave falls and has reflection, the medium of propagation does not change and hence k = k2. Next, we introduce the refractive indices of the mediums:
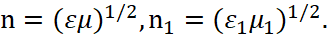(25)
From here we get the known laws of geometric optics:
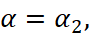(26)
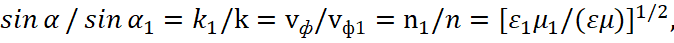
That is, we have the equality of the angles of incidence and reflection and the execution of the Snellius law. According to the formula (26), the magnitudes of the falling wave, of refracted and reflected waves are judged, and here the magnitude of the angle of refraction is calculated from the magnitude of the angle of incidence, taking into account the refractive indices of the mediums. In addition, since the indicators of medium are included in the formulas (22), it was proposed to use them to determine the amplitudes of signals, provided that the indicators of medium are displayed through the angles of incidence and of reflection, taking into account (26). To solve equations (22) and (23), it is convenient to distinguish between two possible cases, depending on whether the vector E has the finding in the surface of falling of vector k or is perpendicular to it. In the first case, when the vector E is lying in the surface of falling of vector k, s obviously significance is (sB) = 0, and equation (22) in accordance with (21) and with the Synellius law (15) gives:
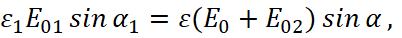
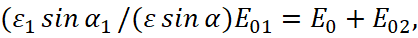
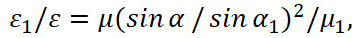(27)
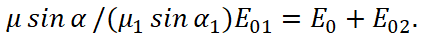
Further, taking into account (23), the formula follows:
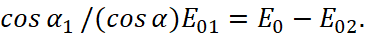(28)
After simple transformations, we find:
(29)
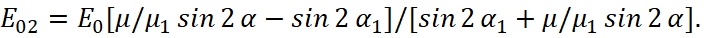
When μ=μ1 these formulas are simplified:
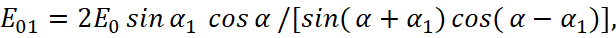
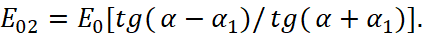(30)
In the second case, when the vector E is perpendicular to the surface of falling of vectors k, s, i.e. (sE) = 0 (Fig. 4), the boundary conditions give results:
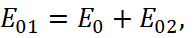(31)
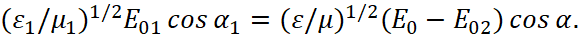
From here, we have:
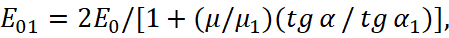(32)
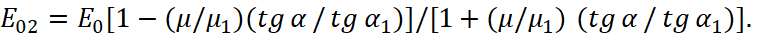
When μ=μ1 these formulas are simplified:
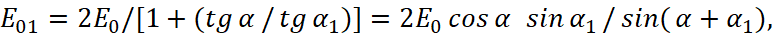
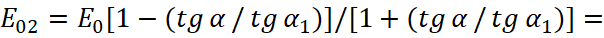
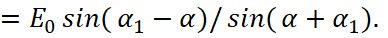
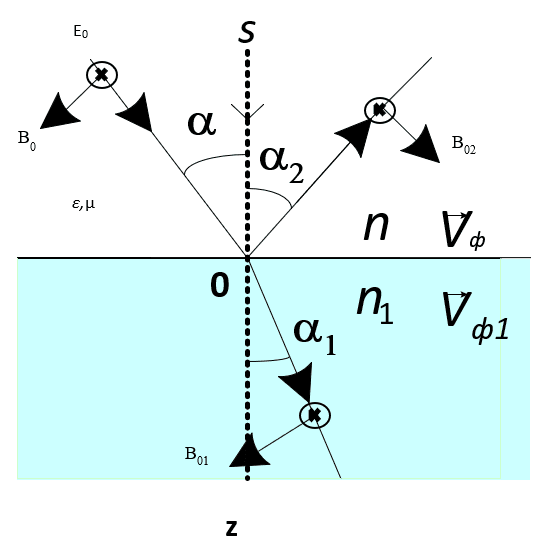
Fig. 4
It is obvious that the falling wave with arbitrary polarization can be represented as a superposition of linearly polarized waves whose polarization vectors either are lying in the flat surface of falling or are perpendicular to flat surface. Thus, any problem of propagation of electromagnetic waves in the presence of a flat surface between two mediums is reduced to the two cases discussed above. Then at falling of the wave along the normal vector, we should put α→0 and, in accordance with the Snellius law, α1=α(n/n1)→0. Then from the formula (29) we get:
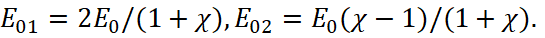(34)
Here we have:
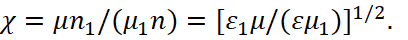(35)
Next, we take into account that the relation is true for the Poynting’s vector:
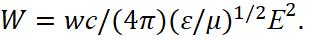(36)
Here w is a unit vector. Hence, it is not difficult to calculate the coefficients of reflection Θ and transmittance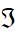 
, which are defined respectively as the ratio of the intensity of reflected and refracted waves to the intensity of the falling wave. Thus we obtain:
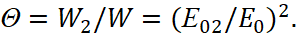(37)
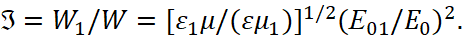(38)
In particular, for a normal fall, according to (34), we find:
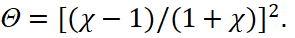(39)
(40)
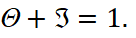(41)
Now it is necessary to consider special cases, for example, when μ=μ1 the wave falls on the boundary at the Brewster's angle α=β, which is being determined by the condition:
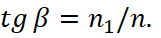(43)
It is obvious that:
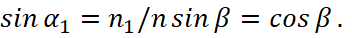(43)
In other words we have:
α1+β=π/2. (44)
Since in this cause tg(α+α1)=∞,
as can be seen from (30) E02 = 0, that is, there is no reflected wave which is polarized in the flat surface of falling. Thus, if the falling wave at Brewster's angle has combination from polarizations, then the reflected wave will be polarized perpendicular to the surface of falling, that is, it will satisfy the condition (nE02) = 0. This phenomenon can be used to produce polarized beams of light in flat surface.
Another interesting phenomenon occurs when a wave falls from a denser medium into a less dense medium (n > n1) at an angle:
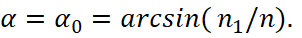(45)
At the same time sinα1=1, that is, α1=π/2. This means that the refracted wave is moving along the border of division of the two mediums. This phenomenon is called a complete internal reflection. In this case, we examine the field in the region z < 0 in more detail. If α>α0, then:
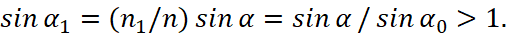(46)
When we have:
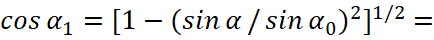
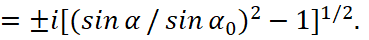(47)
Physically, this means that in the resulting solution describing the field of a refracted wave, the wave vector k1 is imaginary significance. So, considering the flat surface of falling (X, Z), we make sure that the fields E1 and B1 contain multipliers of the form:
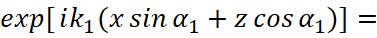(48)
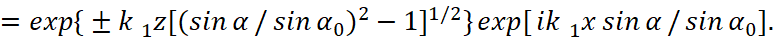
It is further indicated that a solution with sign plus corresponds to a field growing until infinity, and therefore it should be discarded as physically unrealizable. The remaining solution with sign minus (48) describes an electromagnetic wave with fading amplitude. It is clear that the electromagnetic component which has the perpendicular direction to the boundary of the mediums cannot disappear, and the only way is its absorption by particles as in the Compton’s effect. In this case, the wave has propagation along the boundary of division of the two mediums. Accordingly, it is noted that this theory of reflection and refraction of electromagnetic waves can be easily generalized to the case of complex permeability, and in this case the amplitudes of electromagnetic waves contain multipliers of decaying of objects, as with full internal reflection.
It is clear that all options for the reflection and passage of an electromagnetic wave are determined on the base of the angle of incidence and magnitudes of electric and magnetic permeability based on different optic density medium, which is inevitably associated with the movement of the wave at a speed lower than the speed of light. It would seem that, despite the paradoxes of describing processes at the boundary of division of mediums, this provides a practical solution for all cases. However, the resulting mathematics does not give any idea how the absorption of an electromagnetic wave is being obtained, in addition, there is a mathematical solution to the growth of this electromagnetic wave to infinity, which is being discarded. Moreover, at the variant of electromagnetic wave propagation in a gravitational field (vacuum), where the fact of curvature of the direction of motion is and is fixed in practice, there is no change in the significance of the speed of light (с). The change in the magnitude of the speed of light depending on the gravitational field would mean a violation of the Lorentz-Minkowski transformations, where the significance of the magnitude of the gravitational field is determined precisely by the space−time curvature, taking into account the constant in the speed of light.
If we assume a change in the speed of propagation of waves of light depending on the gravitational field, then we must admit a change in the law depending on the space-time curvature and here is the presence of ether, and then we must admit the absence of principle of relativity in SRT of Einstein. Since Einstein's SRT defines an invariant formula associated with the equation of the circle, then changing of speed of light means a violation of the law of conservation of quantity. That is, we come to an open form of universe with infinity with the presence of miracles. Moreover, the fact of a change in the gravitational effect on light is determined by a change in frequency. Actually, the fact of the change in the speed of light in an optically dense medium also has no explanation, since this change would indicate that there is ether. In addition, the Compton’s effect is also known, where the frequency also changes when light is being scattered by free particles [8]. This leads to the problem: "How can we ensure the fulfillment of the law of physics for propagation at the speed of light, with a change in direction in the gravitational field, expressed in terms of space-time curvature?"
Actually, this condition can be fulfilled only if the constants of electric and magnetic permeability change according to the formula:
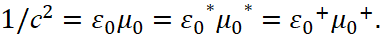(49)
Here, for example, the magnitudes are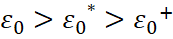 
, and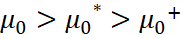 
, or vice versa. In fact, we have a transformation of the formula (35) to the form of taking into account the change in the wave resistance of medium of the propagation in the so-called vacuum:
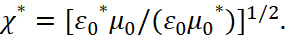(50)
In other words, all the conditions of refraction and reflection based on the constants of electrical and magnetic permeability are observed, and in our case in accordance with formulas (35, 49, 50), since the type of relationship is identical, but at the same time, as it will be seen below, we also have the opportunity to take into account the frequency change during interaction, provided there is no ether. It is clear that we do not explain deceleration of the speed of light in an optically dense medium through changing the speed of movement of light, but the deceleration is determined by the presence of interaction through exchange with radiation and absorption. At the same time, we see the reflection of an electromagnetic wave not as a result of the fact that the same object is being reflected which existed before the fall, but it is necessary to consider the reflected wave as a result of interaction and exchange with border of separation of new medium, where the components are created from interaction of the falling wave with a new medium of propagation with the formation of an electromagnetic wave of refraction and reflected wave. Thus, we take into account the physics of the process instead of fitting to the result. It should also be noted that if in the case of propagation of an electromagnetic wave in a single direction, it is possible the using only of mutual conversion of the electrical component into a magnetic one, and vice versa, but in the case of a change of direction, it is necessary to take into account the transformation taking into account the corpuscular properties with sources of radiation and absorption, that is, space-time curvature, otherwise the rounding by the wave of the obstacle will not be received. In accordance with the analysis, we can draw the following conclusions:
- Fermat's principle does not allow us to describe the change in the direction of an electromagnetic wave in a vacuum and does not explain the reason for the slowing down of the speed of light in an optically dense medium.
- Attempts to describe electromagnetic processes at the boundary of division of the mediums through surface currents and charged particles are associated with the paradoxes described above, and moreover, the conditions of the so-called crosslinking at the boundary of division of the mediums are dependent on the formation of moving waves and waves which are being created in static conditions. And this means no resolving task, but fitting to the result.
- Our theory solves the problem of changing the direction of motion of an electromagnetic wave while maintaining the speed of light, and it does not violate Einstein's SRT. In this case, the magnitudes of the refracted and reflected waves are determined on the basis of changes in the electric and magnetic permeability at the boundary of the mediums themselves without changing their multiplication in each medium which is being associated with the constant of the speed of light.
- A falling electromagnetic wave, a reflected wave and a refracted wave at the boundary of mediums are different objects, because, for example, the formed reflected wave has a new direction, and it means the including of other components which were not present in the falling electromagnetic wave. Hence we have the conclusion that there was an interaction with the medium of division, and the new electromagnetic components were obtained from this interaction, and it gave a new direction. Similarly, this applies to a refracted electromagnetic wave. Such interaction requires the transformation of electromagnetic properties into a space-time curvature, and vice versa, which means the presence of a common electromagnetic and space-time continuum.
- In addition, the interaction in an optically dense medium is associated with the interaction of electromagnetic waves and corpuscular particles, and in this case we are faced with the Compton’s effect, where there is a change of frequency of a photon, and it by means of classical electrodynamics has no description. In classical electrodynamics, the amplitude changes without changing the frequency. This contradicts the presence of a frequency change in the space-time curvature, which is characterized as a gravitational field.
.png&w=640&q=75)
