Звёзды – очень массивные космические тела, излучающие свет. Они образуются из газов и пыли, в результате гравитационного сжатия. Всё это способствует свечению звёзд. Основными характеристиками светил являются спектр, размер, блеск, светимость, внутренняя структура. Также все эти характеристики зависят от положения звезды на небе.
В астрономии нет единого универсального способа определения положения звёзд на небесной сфере. По мере перехода от близких небесных тел к более далёким одни методы определения положения сменяют другие, служащие, как правило, основой для последующих.
Так основным методом определения положения звёзд на небе является фотометрия – это раздел общей физики, занимающийся измерением света. Фотометрия широко применяется как вид молекулярно-абсорбционного анализа, основанного на пропорциональной зависимости между концентрацией однородных систем (например, растворов) и их светопоглощением в видимой, ИК и УФ областях спектра [1].
Именно фотометрический метод и послужил для разработки математической модели нахождения звёзд на небе. Сама модель разработана в среде MathCad.
Для начала необходимо загрузить изображение звёздного неба в MathCad, которое находится в заранее подготовленной папке (рис. 1).

Рис. 1. Исходное изображение части неба
В этом случае изображение имеет размер в 283 строки и 290 столбца. Эти данные также будут необходимы в последствии для дальнейшей обработки изображения.
Для начала проконтрастируем изображение, для этого воспользуемся формулой 1.
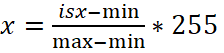 (1)
(1)
где x – проконтрастированное изображение;
isx – исходное изображение;
min, max – минимум и максимум исходного изображения.

Рис. 2. Проконтрастированное изображение части неба
Затем переходим к формированию фильтра, с помощью которого будет определяться местоположение яркостных максимумов звёзд на рисунке 2.
В данном случае воспользуемся фильтром Гаусса. Этот фильтр представляет собой фильтр нижних частот, используемый для уменьшения шума (высокочастотных составляющих) и размытия областей изображения. Фильтр реализован в виде симметричного ядра нечетного размера (DIP-версия Матрицы), которое пропускается через каждый пиксель интересующей области для получения желаемого эффекта [2].
Сам фильтр реализован по двумерной формуле фильтра Гаусса, в данном случае формула 2.
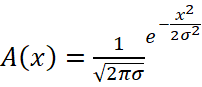 (2)
(2)
После того, как был сформирован фильтр, переходим к этапу корреляции. Корреляция представляет собой статистическую взаимосвязь двух или более случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). При этом изменения значений одной или нескольких из этих величин сопутствуют систематическому изменению значений другой или других величин.
Для расчета меры схожести между гауссоидой с заданными параметрами и изображением воспользуемся формулой нормированной корреляции использовалась формула 3.
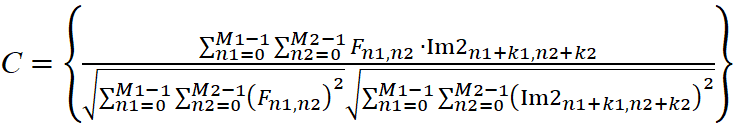 (3)
(3)
В результате получается матрица значений функции корреляции исходного изображения и фильтра Гаусса (рис. 3).
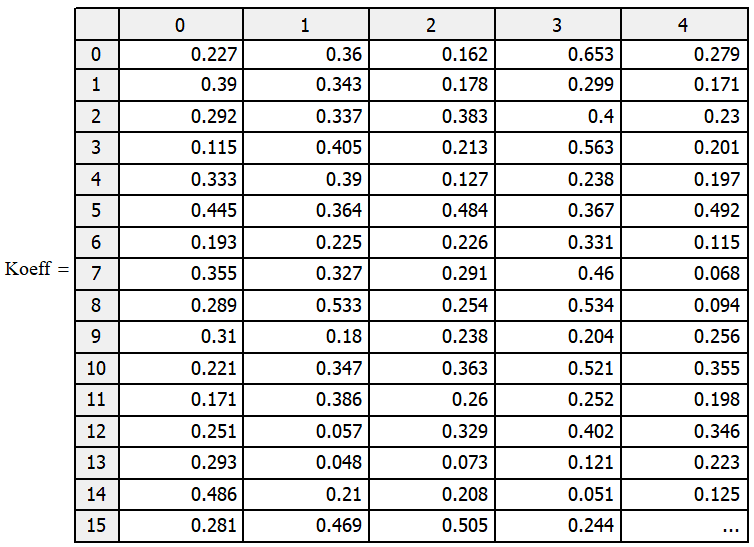
Рис. 3. Матрица значений функции корреляции
Данная матрица имеет значения определённой части исходного изображения. У этой части есть максимум яркости, который составляет 0.939 и находится на пересечении 230 строки и 260 столбца.
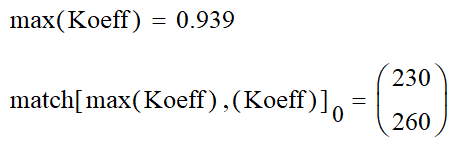
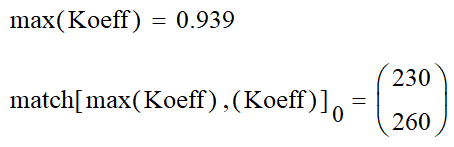
Для того чтобы расчёты можно было делать быстрее, все формулы можно задать одной функцией, которая будет включать в себя фильтр Гаусса и нахождение корреляции между исходным изображением и фильтром Гаусса. При этом данная функция будет накапливать значения положения максимума.
Таким образом, полученная функция, представленная ниже будет одновременно находить значения строк, столбцов, максимумов и яркостей звёзд, которые попадают под значение фильтра Гаусса.
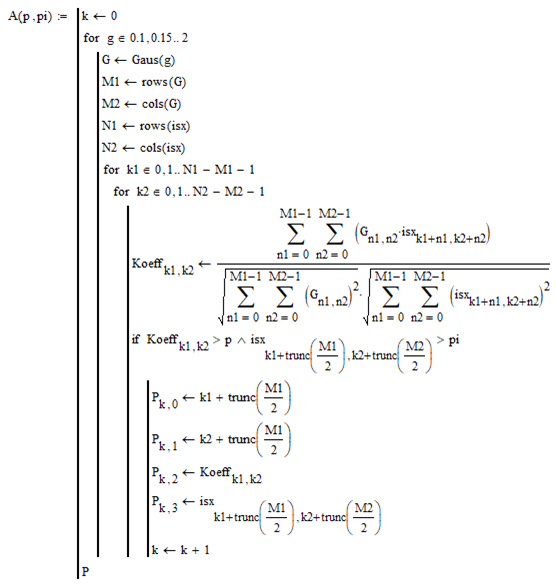
Сама по себе функция имеет три цикла. Первый цикл является основным, в нём задаётся значение параметра g. Этот параметр отвечает за изменение параметра фильтра Гаусса в диапазоне от 0.1 до 2, с шагом 0.05. Первый цикл функции необходим для расчёта значений при текущем параметре g. Второй цикл представляет собой ввод данных для поиска меры схожести между фильтром Гаусса и исходным изображением.
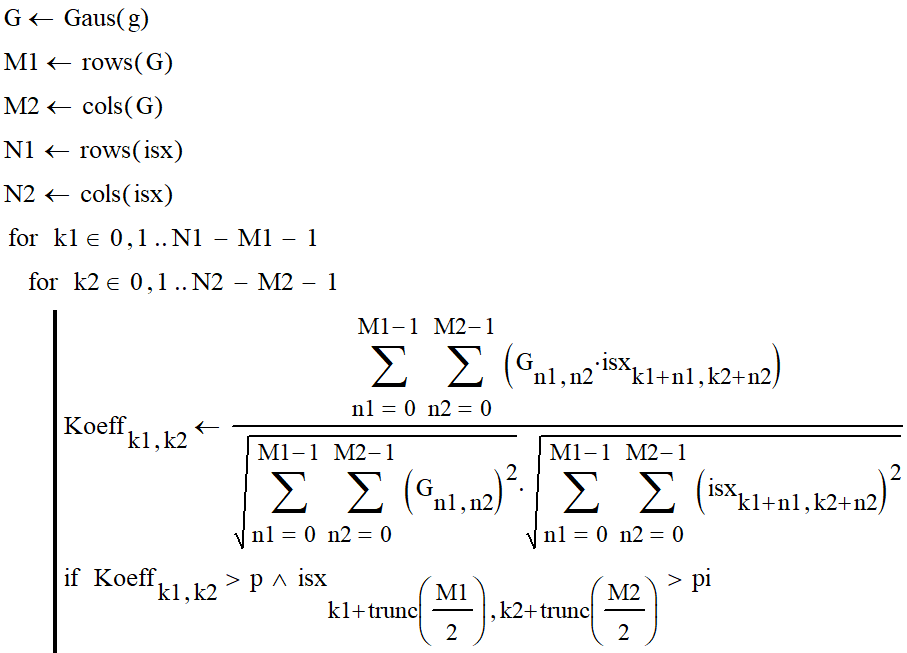
Данный цикл также содержит в себе условие.
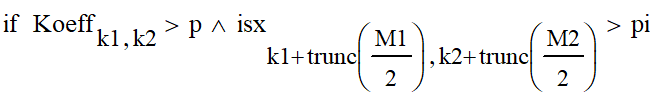
При котором условии, если Koeffk1,k2 будет больше яркости p и больше значения pi, то в данном случае будет выполняться третий цикл. Он необходим, для нахождения строк, столбцов, максимумов и яркостей.
Также в условие необходимо избавиться от дробной части числа с помощью функции trunc. Это необходимо для того, чтобы массив данных накапливал в себе только целочисленные значения.
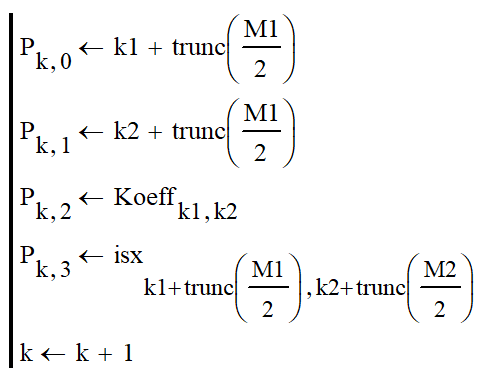
После окончания цикла для данных g находится расположение максимума. Хранение полученных результатов осуществляется с помощью переменных Pk,0, Pk,1, Pk,2, Pk,3.
Так Pk,0 значение предназначено для хранения значения строки, а значение Pk,1 предназначено для хранения значения столбца, значение Pk,2 хранит в себе значение коэффициента максимума. Значение же Pk,3 предназначено для хранения яркости.
Полученную функцию можно представить в виде блок-схемы, приведённой на рисунке 4.
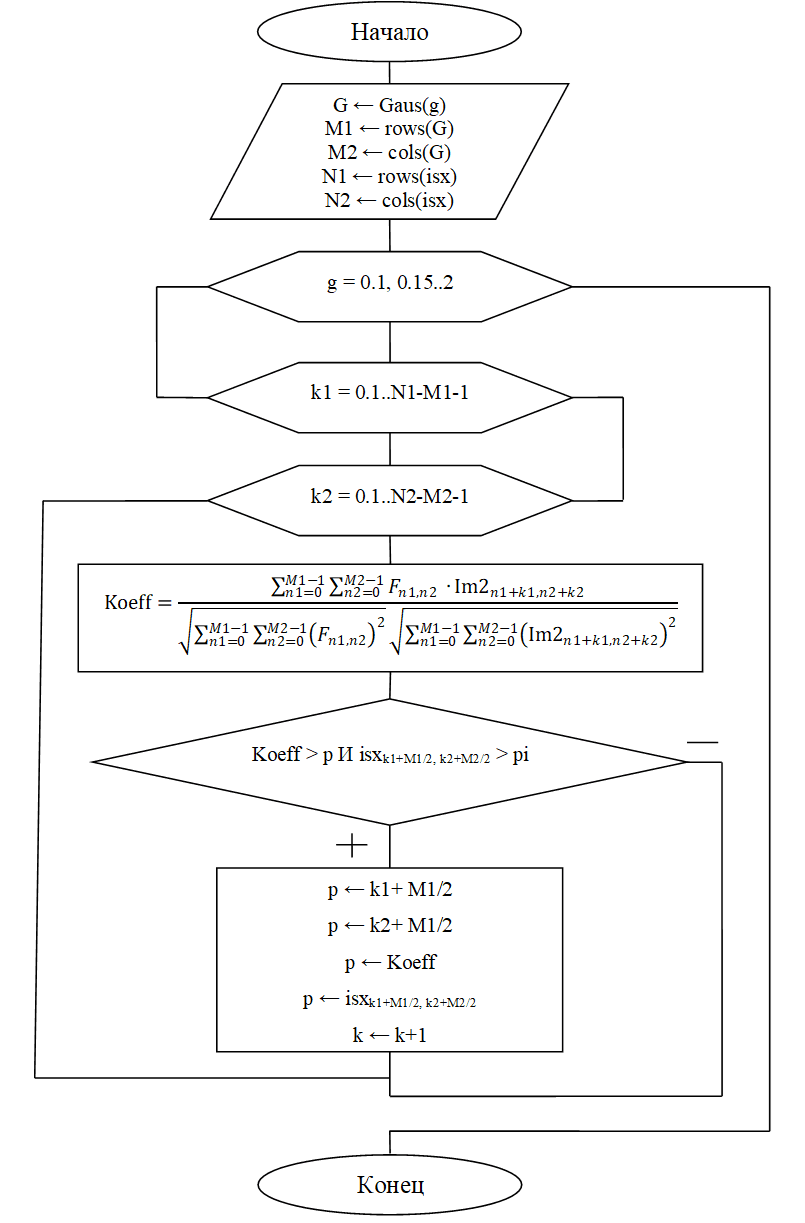
Рис. 4. Блок-схема алгоритма нахождения значения строк, столбцов, максимумов и яркостей звёзд
После нахождения всех значений задаётся порог D, который в этом случае будет равняться D = A(0.9,150). Он определяет значение, по которым будет производиться поиск звёзд.
После этого задаются условия, с помощью которых все найденные значения, приведённые в массиве ниже, будут нанесены на рисунок 5.
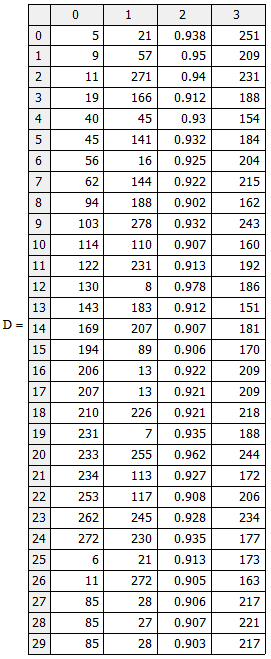
Массив данных хранит в себе значения строк, столбцов, максимумом яркостей и сами значения яркостей. Благодаря этому можно охарактеризовать звёзды, которые были найдены с помощью данной функции. Для этого необходимо воспользоваться табличными данными о значениях светимости звёзд, которые дают полное представление о характере той или иной звезды.

а)

б)
Рис. 5. Результат обработки изображения а) полученное изображение, б) исходное изображение
Таким образом, при сравнении полученного и исходного изображений, можно сказать, что не все звёзды были определены. Это связано с тем, что фильтр Гаусса имеет достаточно малый размер, а также заданный порог отсекает многие звёзды, которые не подходят по этому параметру.

.png&w=640&q=75)