Вначале опишем эффект Комптона, как это представлено в квантовой механике [1]. Эффект Комптона интересен тем, что в нём соблюдается не только закон сохранения энергии, но и закон сохранения импульса. При этом используется формула Луи де Бройля: Е=mc2=hf для определения изменения частоты после столкновения фотона и частицы. Сам принцип закона сохранения импульса не столь очевиден, как закон сохранения энергии в силу того, что электрон и позитрон при аннигиляции и при отсутствии импульсов могут формировать фотоны с наличием импульсов в направлении их движения пропорционально их энергии. Понятно, что чудом возникнуть импульсы фотонов в направлении движения не могут. Отсюда остаётся предположить, что закон сохранения импульса соответствует интерпретации формирования корпускулярных частиц на основе замкнутого движения электромагнитного состояния, что проявляется в аннигиляции электрона и позитрона с появлением фотонов, и обратном возникновении электрона с позитроном при столкновении фотона соответствующей энергии с препятствием. Иными словами, импульсы фотонов при столкновении с частицами не исчезают, а переходят во вновь образовавшихся частицах в замкнутое состояние, и наоборот, при аннигиляции частиц есть переход от замкнутого состояния в разомкнутое. Для подтверждения этих слов мы в этой статье покажем связь электромагнитных составляющих с массой и скоростью. Как известно, в классической теории электродинамики при рассеянии света свободными электронами, его частота не изменяется (ω'=ω). Может уменьшиться лишь интенсивность падающего пучка, так как часть энергии идёт на раскачку электронов без изменения частоты. Это даёт парадокс закона Снеллиуса, в котором амплитуда интенсивности падающей волны, отраженных и преломленных волн на границе раздела поверхностей зависит от значений электрической и магнитной проницаемости при сохранении значения частоты в соответствии с классической электродинамикой. По квантовой теории часть энергии фотона E=ℏω также передаётся электрону, но с изменением частоты, а не интенсивности падающего пучка как в электродинамике. Поэтому, энергия рассеянного фотона E'=ℏω', а вместе с тем и его частота, должны быть несколько меньше (E'<E, ω'<ω). Данная разница объясняется тем, что в классической электродинамике учитывается только волновое представление фотонов, а в квантовой механике фотоны рассматриваются как частицы, при этом частоту связывают с массой, а значит и энергией, на основе формулы Луи де Бройля.
В соответствии с квантовой механикой, чтобы найти зависимость частоты от угла рассеяния по эффекту Комптона, напишем законы сохранения энергии и импульса, рассматривая не только электроны, но и фотоны как частицы (рис.1):
ℏω–ℏω'=с2(m–m0) (1)
ℏk–ℏk'=mv. (2)
Здесь m0 и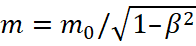 
‒ масса электрона соответственно до (электрон покоится) и после столкновения, n ‒ вектор скорости; β=v/c; ℏk=ℏω/c и ℏk=ℏω'/c ‒ импульс фотона соответственно до и после рассеяния.
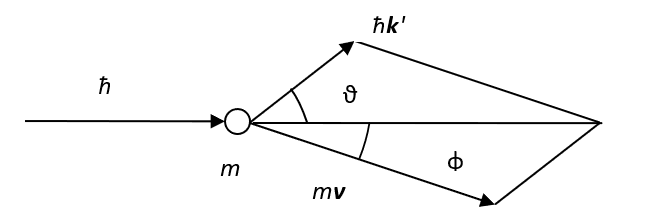
Рис. 1. Рассеяние света на свободном электроне
Перепишем уравнения (1) и (2) в виде:
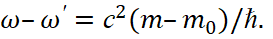(3)
k–k'=mv/ℏ. (4)
Далее возводим эти равенства в квадрат:
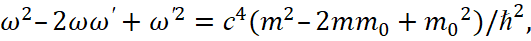(5) 
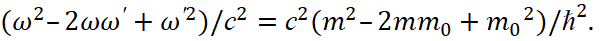
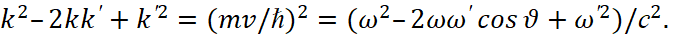(6)
Вычтем равенство (5) из равенства (6), получаем:
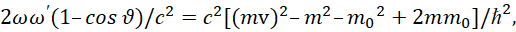
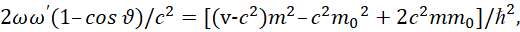
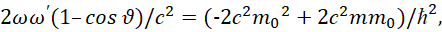
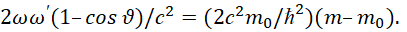(7)
С учётом подстановки (3) имеем:
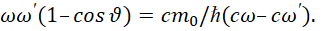(8)
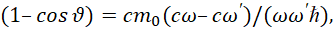
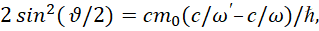(9)
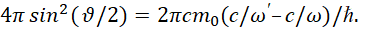
Далее учтём, что длина волны λ=2πc/ω и λ'=2πc/ω', а комптоновская длина волны λ0 электрона равна:
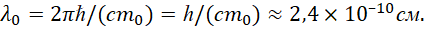(10)
В результате следует равенство:
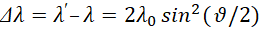(11)
Из формулы (11) мы видим, что здесь есть три свободных взаимосвязанных параметра: λ ‒ первоначальная длина волны фотона, λ' ‒ длина волны фотона после столкновения с электроном и угол рассеяния ϑ. Как известно комптоновское рассеяние экспериментально наблюдалось при сравнительно малых длинах волн (рентгеновское излучение, гамма-кванты):
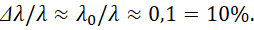(12)
Комптоном был проведён эксперимент для различных рассеивающих веществ (рис. 2). Графики результата эксперимента приведены на рис. 3‒5 [2], где в качестве рассеивающего вещества выступал молибден (Mo).
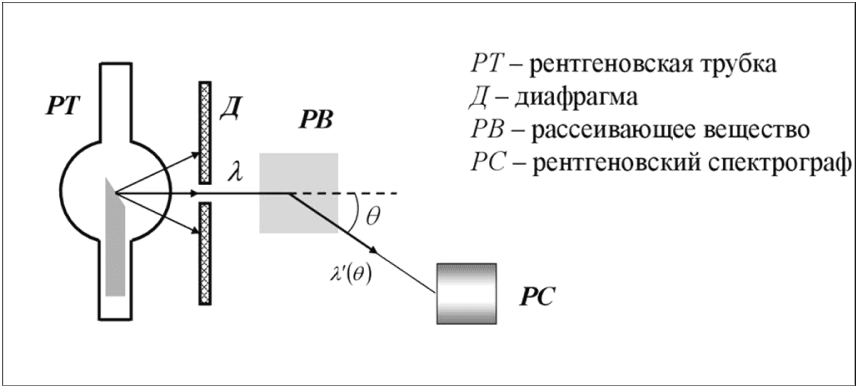
Рис. 2. Схема эксперимента
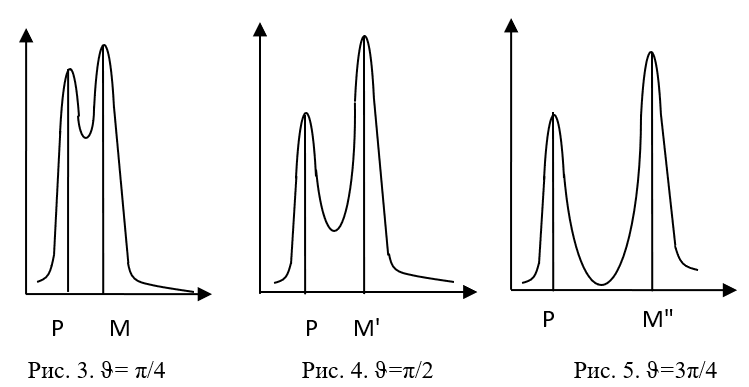
При угле рассеивания ϑ=0 отмечалось только прохождение несмещённой компоненты рентгеновского излучения (на графиках эта компонента обозначена буквой Р). По сути это означает, что фотон не взаимодействует с электроном, так как при вычитании (5) из (6) при ϑ=0, мы в левой части уравнений (7) получим ноль, а это означает, что никакого добавочного импульса электрон получить не может, либо он его получил и тут же отдал. Однако при углах рассеивания от ϑ= π/4 до ϑ=3π/4 наблюдается появление смещённой компоненты в сторону увеличения длины волны под буквой М. Причём смещение тем, больше, чем больше угол рассеивания. Отметим, что при рассеивании веществами с малыми атомными номерами (Li, Be, B) практически всё рассеянное излучение имеет смещённую длину волны. По мере увеличения атомного номера всё большая часть излучения рассеивается без изменения длины волны.
По мнению учёных, особенности эффекта Комптона можно объяснить, рассматривая рассеяние как процесс упругого столкновения рентгеновских фотонов с практически «свободными» электронами. Свободными можно считать слабее всего связанные с атомами электроны, энергия связи которых значительно меньше той энергии, которую фотон может передать электрону при соударении. При этом отмечается, что при упругом соударении фотон не может передать электрону (или какой-либо другой частице) всю свою энергию. Такой процесс нарушал бы закон сохранения энергии и импульса.
Видно, что само понятие упругого столкновения не раскрывает механизм взаимодействия, а есть лишь утверждение. Кроме того, утверждение, что «при соударении фотон не может передать электрону всю свою энергию» также сомнительно, так как известно, что при столкновении фотона (γ) соответствующей частоты с электроном или ядром возможно образование пары электрона (e–) и позитрона (e+) по схеме [3]:
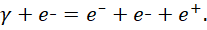(13)
И в этом случае энергия и импульс фотона отдаются электронам и позитрону без наличия после столкновения при этом фотонов. А это означает, что отсутствие фотона после соударения соответствует тому, что передача его энергии произошла полностью. Понятно, что при аннигиляции электрона с позитроном мы должны иметь также сохранение импульсов в фотонах. Отсюда делаем выводы относительно эффекта Комптона:
- Парадокс с точки зрения классической электродинамики связан с тем, что описать изменение частоты невозможно в силу ассоциативного сложения и вычитания электромагнитных волн. Изменение частоты, а значит и фазы, однозначно связано с нелинейными преобразованиями, что определяется переходом из одной противоположности в другую. А так как сложение в одной противоположности представляется вычитанием, то здесь есть переход количества в качество (изменение закономерности). Ассоциативное сложение перехода количества в новое качество не даёт. При этом ассоциативное вычитание электромагнитных волн приводит к парадоксу отсутствия дальнейшего распространения волн при интерференции при обнулении амплитуд напряжённости электромагнитных полей.
- Парадокс с точки зрения квантовой механики ‒ это понятие упругого столкновения, которое не имеет физического описания при утверждении, что «при соударении фотон не может передать электрону всю свою энергию». Понятно, что при неупругом столкновении фотон должен исчезнуть с исчезновением свойств частицы. Кроме того, надо представить фотон в корпускулярном виде, а как, если с точки зрения классической электродинамики он имеет только электромагнитное описание?
Отметим, что главное условие для упругого столкновения с полным исключением исчезновения фотона ‒ это соблюдение закона сохранения энергии и импульса. Однако, если исходить из классической механики, по закону сохранения импульса для корпускулярных свойств частиц, импульс фотона в направлении движения должен передаваться либо полностью (как при столкновении двух шаров), что даёт парадокс наличия фотона без импульса, либо часть фотона должна отражаться при столкновении. И здесь, никоим образом не могут возникнуть из нуля, две составляющие импульса в противоположных направлениях, что видно в рис.1, так как фотон их не имел до столкновения. Собственно для появления противоположных импульсов в физике известен процесс аннигиляции электрона и позитрона, но в данном случае аннигиляции нет, так как нет и зарядов.
Таким образом, парадоксы эффекта Комптона заключаются в том, что нет обоснования такому преобразованию фотона и движению электрона после столкновения ни с точки зрения чисто корпускулярных свойств и квантовой механики, ни с точки зрения классической электродинамики.
Чтобы разрешить указанные парадоксы надо показать преобразование корпускулярных свойств в волновые, и наоборот, но сделать это при придуманных "штампах", которые были применены при начальном развитии физики и математики невозможно. Действительно, представленный выше переход от законов сохранения импульса и энергии не даёт представления к физическому принципу изменения частоты фотона при соударении с частицей. Иными словами надо показать как элементарные законы физики, на основе которых строится практика любых расчётов, приводят к эффекту Комптона.
Решение задач в физике и математике должны быть от простого варианта к сложному варианту, и при этом соответствовать практическим результатам. Ещё М. Ломоносов открыл закон, по которому объект состоит из того, на что он распадается, а это как раз и подразумевает переход от простого варианта к сложному варианту. Однако вопреки М. Ломоносову придумали кварки и глюоны, даже не зная их принцип взаимодействия и которые при распаде не наблюдаются, более того взаимодействие представили в виде телепортации через потенциальный барьер не сумев решить задачку поглощения и излучения в электродинамике! Поэтому начнём с элементарного процесса известного на практике, из которого можно сделать выводы по однозначной теории. Так хорошо известно, что электрон и позитрон при аннигиляции дают фотоны - электромагнитные волны. Одновременно при распаде мюонов и пионов наблюдаются электронные и мюонные нейтрино и антинейтрино и это реальные объекты. Так как, исходя из той же практики, положительные и отрицательные пионы и мюоны, а также протоны и антипротоны дают при аннигиляции те же фотоны, то следует вывод, что электронные и мюонные нейтрино и антинейтрино в частицах взаимодействуют с получением дополнительной массы и могут давать в результате взаимодействия и электромагнитную волну. Иными словами наипростейшими объектами являются электронные и мюонные нейтрино и антинейтрино. Покажем всю логическую цепочку подтверждения этого вывода. Для описания электромагнитных волн в физике был использован практический закон Фарадея, который имел математическое описание в виде:
rot E=–∂B/∂t. (14)
Однако этот закон описывал частный случай взаимодействия без описания соответствия и связи с реально существующими объектами, и конечно получить из него уравнение электромагнитной волны не представляется возможным. Кроме того, такая запись имела парадокс, в соответствии с которым электромагнитная энергия имела описание по уравнению Умова-Пойтинга вида:
∂W/∂t=–div S. (15)
Это означает, что изменение энергии во времени даёт и изменение энергии в пространстве. Уравнение (14), наоборот, говорило о том, что изменение во времени не даёт изменение в пространстве из-за замкнутости процесса по напряжённости электрического поля. Но, электрическая и магнитная составляющие однозначно связаны с энергией электромагнитного поля, так как иное исключало бы и силовое воздействие этих полей без наличия энергии. То есть, здесь получается двойственность, что и даёт парадокс, а это означает, что используемый на практике закон Фарадея не имеет физической законченности и представляет частный случай одностороннего превращения энергии, то есть мы имеем действие без противодействия. Ситуацию решил исправить Максвелл и ввёл симметрию в виде уравнений:
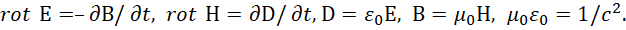(16)
Отсюда путём упрощений получалось два отдельных уравнения для электромагнитной волны за счёт подстановки одного уравнения Максвелла в другое, что, кстати, и даёт взаимодействие. При этом уравнения выглядят так:
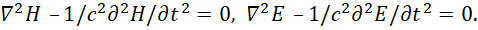(17)
Но, парадокс здесь в том, что получаются два независимых уравнения, что в принципе исключает необходимость взаимодействия электрических и магнитных составляющих, и кроме того, нет возможности огибания волной препятствия, что наблюдается на практике. То есть, требовалось доработать уравнения Максвелла, и это было сделано за счёт сторонних (фиктивных токов) в виде [4]:
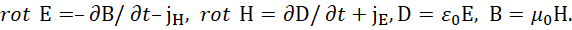(18)
Однако возник парадокс, по которому наличие фиктивных токов равносильно чуду, так как не ясен физический смысл их образования без привязки к дифференциальным изменениям в обычных уравнениях Максвелла. То есть, если нет описания фиктивных токов через приращения в пространстве и времени с представлением их в виде электромагнитных составляющих, то мы имеем эквивалент образования из ничего, что означает чудо. Поэтому потребовалось обоснование этих токов в соответствии с уравнениями Максвелла на основе электромагнитных составляющих. Именно эта проблема и была рассмотрена в [5] с выводом усовершенствованных уравнений Максвелла через вектор-потенциалы. Однако в [6] мы установили, что для исключения парадокса закона Снеллиуса с учётом поглощения и излучения требуется наличие комплексных значений электрических и магнитных проницаемостей для описания взаимодействия со средой распространения. Поэтому покажем вывод усовершенствованных уравнений Максвелла на основе комплексных значений. С этой целью выберем одно из известных уравнений Максвелла в частных производных в виде:
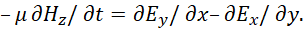(19)
При представлении в электродинамике значения магнитной проницаемости в комплексном виде имеем: μ= μо+iμо, как комплексной величины (здесь i=(-1)1/2) в силу взаимодействия со средой по принципу Гюйгенса-Френеля. При этом, значение μо одинаковой величины в действительной и мнимой части, так как среда не изменяет объект движущийся со скоростью света, иначе объект распадается или будет расти до бесконечности (это было показано в [6]), в силу отсутствия закона сохранения количества. То есть, принцип термодинамического равновесия не может нарушаться в среде распространения аналогичного так называемому вакууму, так как это приводило бы к наличию ультрафиолетовой катастрофы с наличием бесконечных значений. Иными словами среда распространения характеризует взаимодействие без изменений с соблюдением равенства действия и противодействия. Отсюда получаем:
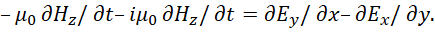(20)
По сути, данный вид записи соответствует представлению фиктивного тока jH в уравнении (18) в виде равенства jH =iμо∂Нz/∂t и это также показано в [4], где Нz= Нст. Однако данный вид записи имеет парадокс, связанный с тем, что мы имеем одинаковое представление производной напряжённости магнитного поля по координате z. В [4] данное представление в (20) имеет вид:
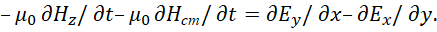
То есть, о каком действии и противодействии, и противоположностях может идти речь, если одна и та же величина отображается одинаково в противоположностях? Практически мы имеем в левой части равенства чудо добавленного члена вида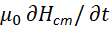 
. Что в этом случае может воздействовать и противодействовать, если нет никаких изменений и преобразований? Если нет никаких преобразований, то нет отличий, а значит и самого перехода в противоположность. Однако и в уравнении (20) нет разницы в представлении противоположностей кроме атрибута мнимой единицы, а это означает однородность. По нашей теории глобальные противоположности связаны через скорость света (скорость изменения), что кстати тоже ввели не мы первые, поэтому умножаем числитель и знаменатель мнимой производной на скорость света (с):
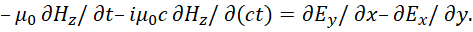(21)
То есть, в соответствии с наличием атрибута противоположности в виде мнимой единицы (i) делаем переход в противоположность через скорость света, так как противоположности связаны через скорость света (скорость изменения). Это аналогично записи связи глобальных противоположностей длины и времени в квантовой механике в виде х=ict, то есть такой способ перехода от времени к длине, и наоборот, были вынуждены использовать ещё до нас в квантовой механике [7]. Таким образом, наличие противоположности характеризуется мнимой производной, а за счёт скорости света длина и время, которые и отражают глобальные противоположности, меняются местами. Повторим, что одинаковый вид исключает наличие противоположностей. Кроме того, если бы при преобразованиях Лоренца-Минковского время преобразовывалось в длину, а длина во время не в равных количествах, то тогда осталась бы только длина или время и мы бы не имели противоположностей связанных через скорость света. То есть, среда – это не некий вакуум, а это противоположности, выраженные через длину и время и имеющие закон связи через преобразования Лоренца-Минковского по СТО и ОТО Эйнштейна. Иначе и говорить не о чём без этих величин, попробуйте выразить любой объект без описания по длине и времени. При преобразованиях соблюдается равенство (иначе что-то одно должно исчезнуть), отсюда μо =iμо, где мнимая единица i выступает как атрибут противоположности и фактически выражает закон по которому на действие одной противоположности происходит противодействие, что и выражается возвратом со знаком минус. С учётом того, что противоположности связаны через скорость света (скорость обмена), то покой и движение в противоположности также меняются местами, а это выражается и сменой проекций, где длина переходит во время, а время в длину. Проекция напряжённости магнитного поля по z в мнимой производной может однозначно преобразовываться только в проекцию по времени, а проекция по времени преобразуется в проекцию по длине по координате z. Преобразование времени должно быть связано с переходом в противоположность по координате z в соответствии с СТО и ОТО Эйнштейна, и тогда замкнутости в правой части уравнения (21) будет соответствовать замкнутость и в левой части уравнения с выполнением закона сохранений количества. Кроме того, если бы не было проекции напряжённости магнитного поля на время при преобразованиях Лоренца-Минковского по СТО и ОТО Эйнштейна, то это бы означало разрыв и независимость электромагнитного поля от преобразований по длине и времени, что исключило бы возможность изменения направления электромагнитной волны в пространственно-временном искривлении. Отсюда имеем усовершенствованное уравнение Максвелла:
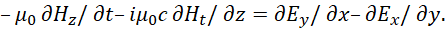(22)
Собственно изменение по времени всегда связано с движением (иначе уравнение Умова-Пойтинга не имело бы практического подтверждения), а любое движение обязано подчиняться преобразованиям Лоренца-Минковского по СТО и ОТО Эйнштейна с переходом длины во время и наоборот. Здесь в силу перпендикулярности составляющих Е и Н остаётся только одно изменение в пространстве по направлению z.
Это уравнение (22) обосновывает физически введение в уравнения Максвелла фиктивных (сторонних) токов с представлением в дифференциальном виде с проекциями электрических и магнитных составляющих на время. Иными словами, введённые новшества в уравнения Максвелла, касались учёта того, что логически уже было введено в физику, это представление связи времени и длины в квантовой механике в виде х=ict [7], и замене в уравнении Максвелла при сторонних токах в частных производных значения Нст на Нt в соответствии с выполнением СТО и ОТО Эйнштейна. Однако даже эти элементарные логические выводы, введённые практически до нас, отказываются признавать так называемые «корифеи науки» даже не имея альтернативы чуду, введённому через сторонние токи и напряжённости электрических и магнитных полей. Отсюда также следует, что урезанный вид уравнений Максвелла без фиктивных токов не позволяет перейти к уравнениям волны с огибанием препятствий на основании принципа Гюйгенса-Френеля, и это означает, что усовершенствованные уравнения Максвелла являются минимально возможными уравнениями, которые могут описывать реальные объекты, например, такие как электронные и мюонные нейтрино и антинейтрино. Как было показано в [5] через подстановку одних уравнений в другие, это решает проблему связи электрических и магнитных компонент и огибания волной препятствий на основе фиктивных токов в виде:
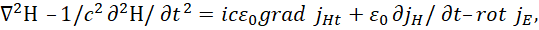(23)
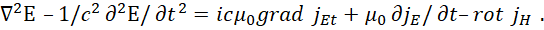
Аналогичный вид через фиктивные (сторонние) токи есть и в классической электродинамике при наличии комплексного вида, но с взятием производной по времени [8].
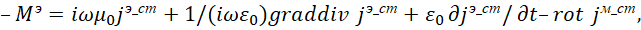
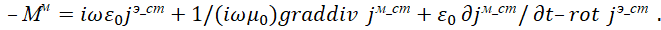(24)
Здесь мы имеем уравнения Гельмгольца в виде:
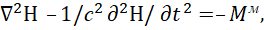(25)
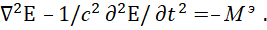
Понятно, что значения Мм и Мэ должны иметь представление в виде волновых электромагнитных составляющих, как исходные значения электромагнитных волн, то есть Мм=Нм и Мэ=Еэ. В противном случае надо иметь алгоритм преобразования значений, то есть иное представление не в виде одного обозначения, чего в данном случае нет, как, например, в случае со сторонними токами.
Одновременно в классической электродинамике, известно также и представление уравнений волны через вектор-потенциалы и сторонние токи, заряды в виде уравнений [9]:
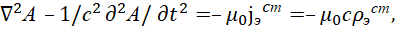
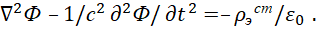(26)
В соответствии с квантовой механикой [10]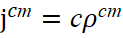 
. Если учесть, что наименьшая плотность заряда не может быть меньше заряда электрона или позитрона в соответствии с тем, что по теории Дирака в уравнении энергии Эйштейна 
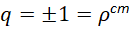[11], то получим уравнения вида:
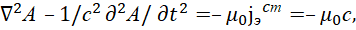
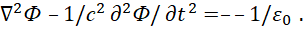(27)
Отсюда следует, что волновые функции вектор-потенциалов определяются значениями констант электрической и магнитной проницаемости. Это неудивительно, так как вектор-потенциалы однозначно связаны с электромагнитными функциями в виде:
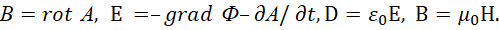(28)
Собственно такой связи электромагнитных функций с вектор-потенциалами есть физические аналоги и это даёт реальную необходимость вектор-потенциалов. Для первого уравнения в (28) физическим аналогом является закон Био-Савара-Лапласа:
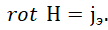(29)
По сути, этот закон означает, что прямолинейное движение в одной противоположности даёт замкнутое движение в другой противоположности.
Второе уравнение в (28) отображает обратный процесс в виде гармонического осциллятора или волнового уравнения, когда, наоборот, замкнутое движение в одной противоположности даёт излучение (прямолинейное движение) в другой противоположности по формуле [12]:
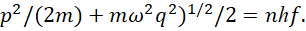(30)
Соответствие легко установить если учесть, что понижение уровня дифференцирования второго порядка обеспечивается заменой переменных аналогично виду для сторонних токов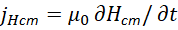 
. Сам вывод волновых уравнений был сделан из уравнений Максвелла вида:
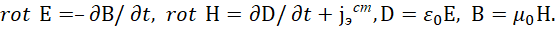(31)
Иными словами, здесь устанавливается связь электрических вектор-потенциалов А и Ф в волновом виде с наличием электрического стороннего тока в нашей системе наблюдения и электромагнитных функции. При этом данный сторонний электрический ток является реальным воплощением действующего тока, который в нашей системе наблюдения отражает взаимодействие противоположностей по длине и времени, которые представлены в виде так называемых электрических зарядов. В [13] на основании электромагнитного континуума была показана однозначная связь зарядов как объектов, отражающих противоположности длины и времени с учётом подчинения СТО и ОТО Эйнштейна. Так как здесь мы имеем симметрию между волновым видом электромагнитных составляющих и вектор-потенциалами, в левой части уравнений (25) и (26), следует вывод, что есть поглощение энергии средой, и есть её отдача (так как нет равенства между вторыми производными по времени и длине), а это без излучения и поглощения быть не может. Мы видим, что характеристики источников поглощения и излучения выражены через константы электрической или магнитной проницаемости и определяют пространственно-временное изменение под внешним воздействием. В противном случае этих констант не было бы для описания процессов электромагнитного взаимодействия в среде. Так как внешняя среда, где распространяется электромагнитная волна, называется вакуумом и описывается по СТО и ОТО Эйнштейна пространственно-временным искривлением, и ничего другого нет, то остаётся предположить, что электрическая и магнитная проницаемость описывают именно это пространственно-временное искривление. Так как движение объектов в так называемом вакууме не наблюдается (нет ничего, чтобы имело описание помимо представления в виде длины и времени), а искривление описывается через скорость, то остаётся предположить, что эта скорость относится к скорости в противоположности и она является проекцией скорости на время, что при связи противоположностей через скорость света даёт абсолютную систему отсчёта для ОТО Эйнштейна. Именно отсутствие понимания наличия противоположности связанной с нашей системой наблюдения через скорость света привело к ошибочному мнению существования некой отдельной массы внутри пространственно-временного искривления. Отсюда константы электрической и магнитной проницаемости могут быть выражены через некую среднюю обобщённую (интегральную) скорость vпр (связь противоположностей через интегрирование также ввели не мы, это было сделано в квантовой механике, что будет показано несколько ниже). То есть константы электрической и магнитной проницаемости связаны с проекцией скорости на время, так как ни одна величина не может описываться вне компонент принадлежности по пространству и времени. Иначе vпр не соответствует принципу корпускулярно-волнового дуализма и не является реальной величиной описывающей объект. Следовательно, vпр определяет среднюю интегральную кинетическую энергию в противоположности по формуле:
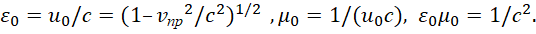(32)
В этом случае при m0=1/c (это будет показано несколько ниже), имеем:
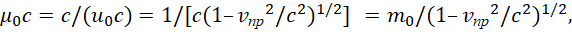
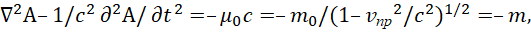
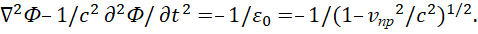(33)
По логике от второго уравнения в (33), знак минус перед значением m будет соответствовать поглощению, а знак плюс излучению электромагнитной волны. Собственно любой реальный объект должен излучать и поглощать для взаимосвязи с другими объектами, иначе он не существует. В противоположности вектор-потенциалы отображают электромагнитные процессы, и тогда А=v/c2=Ф/с (при v=c) [14], и при приведении к одинаковому виду с учётом исключения связи через скорость света будем иметь одинаковый вид, что означает, что преобразования вектор-потенциалов, а значит и электромагнитных составляющих в противоположности, происходит с законом сохранения количества, что подтверждает принцип взаимного наведения и перехода друг в друга. Отсюда следует вывод, что составляющие А и Ф, которые в противоположности характеризуют электромагнитные процессы, что соответствует по физике наличию волн Луи де Бройля, при поглощении формируют так называемую массу в представлении искривления пространства и времени на основании vпр. По сути это может восприниматься как формирование заряда одного знака (одной противоположности характеризующей или длину или время), который сформирован в результате замкнутого обмена вектор –потенциалов А и Ф. Как будет показано ниже формирование заряда другого знака (противоположности) будет определяться вектор – потенциалами Ам и Фм. Формирование волнового процесса в зависимости от массы определяет связь массы и частоты по формуле Луи де Бройля. Однако в эффекте Комптона участвует закон сохранения импульса помимо закона сохранения энергии, поэтому выведем связь скорости и массы исходя из замкнутого преобразования двух противоположностей на основе уравнения окружности (другого закона с сохранением количества при взаимном обмене просто нет).
Собственно, при условии сохранения объекта, динамика взаимодействия противоположных частей объекта, с учётом наблюдения из одной выбранной противоположности, будет выглядеть в нормированном к максимальной скорости обмена виде:
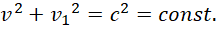(34)
Перепишем полученное уравнение в ином виде:
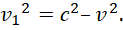(35)
Далее произведем следующие преобразования:
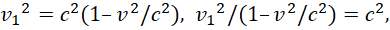
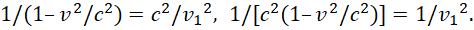(36)
Сделаем замену переменных и считаем, что m=1/v1, а m0=1/c. В итоге имеем:
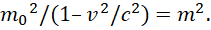(37)
Если умножить оба члена указанного уравнения на величину c4 (что не меняет сути уравнения), то получим формулу энергии Эйнштейна в квадрате. Учитывая, что в формулу Эйнштейна входят только две переменные величины, которые дают замкнутую систему по формуле окружности, то они и являются противоположностями друг для друга (аналогично длине и времени, которые связаны через скорость света [15]), т.е. могут преобразовываться только друг в друга. А отсюда следует, что указанные величины не могут выражаться через один и тот же вид, иначе такое преобразование ничем не зафиксировать в силу отсутствия различий между противоположностями. Поэтому, если одна переменная величина выражает скорость v, то второй изменяемой переменной остаётся роль массы и при этом v1=1/m. Далее отметим, что замкнутость мироздания определяет равенство константе. Ноль и бесконечность исключают наличие любых законов физики, а также и постоянство скорости обмена (скорости света). И если мироздание является константой, то обмен между глобальными противоположностями может проходить только с одной постоянной скоростью, а иначе мироздание автоматически становится закономерностью и, соответственно, не может быть замкнутой величиной. Ограничение шага дискретизации константой постоянной Планка исключает однородность, и иное связано с наличием «ультрафиолетовой катастрофы» с ростом энергии до бесконечности. При замкнутости мироздания на две глобальные противоположности шаг дискретизации тоже автоматически следует из постоянства скорости обмена. Отметим, что определить скорость обмена для бесконечно малого объекта не представляется возможным. Так, задавшись величиной минимального объекта N и определив его скорость передачи как S, мы при наличии бесконечно малых объектов всегда можем представить этот объект как N=kn, где n – это еще меньший объект. Соответственно, скорость передачи для объекта n должна быть выше в k раз, чтобы для общего объекта N получить значение скорости обмена равное S. В этом случае нет и предела скорости обмена. Быстроногий Ахиллес никогда не догонит неторопливую черепаху, если в начале движения черепаха находится впереди Ахиллеса. При этом мы напоминаем, что любые изменения у нас связаны с переходом в противоположность, поэтому вариант с движением в одной противоположности, например, движение поезда, здесь не подходит, так как в этом случае рассматривается вариант без взаимодействия с противоположностью, то есть отрицается необходимость самих противоположностей.
Отсюда вывод: замкнутость мироздания определяет и значение максимальной скорости обмена (света) и значение минимального шага дискретизации, что определяет и наличие единичных объектов воздействия. Константа мироздания определяется величиной произведения скорости обмена на шаг дискретизации.
В противном случае были бы единичные элементы, которые не участвуют в обмене, а значит, независимы от процессов в мироздании. Такая независимость означает отсутствие взаимодействия, а взаимодействие означает обмен. Поэтому, если единичный объект не принимает участие в обмене, то он и не взаимодействует, и значит, независим. Но участие в обмене определяется скоростью. Поэтому скорость обмена должна быть такова, чтобы изменению подверглись все единичные элементы мироздания. А иначе неохваченные элементы автоматически становятся независимыми.
Отсюда получаем: произведение скорости света (с) на постоянную Планка (h) определяет значение константы нашего мироздания по взаимодействию:
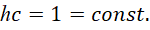(38)
Здесь мы имеем следующую логическую цепочку. Замкнутость мироздания определяет постоянство скорости обмена при взаимодействии, что приводит и к наличию минимального шага дискретизации. Так как взаимодействие возможно только в случае обмена, то исключить независимость отдельных элементов можно только тогда, когда общий количественный обмен, который и характеризует энергию взаимодействия, определяется по формуле произведения скорости света и постоянной Планка!
Отметим, что необходимость связи скорости света с постоянной Планка уже была введена до нас как постоянная тонкой структуры [16]:
(39)
Разница лишь в нормировке, и её можно пересчитать, если учесть, что заряд q по теории Дирака можно считать равным плюс или минус единице, так как его нет в формуле энергии Эйнштейна, и его роль сводится к представлению операции излучения или поглощения, то есть не количества, а действия-закономерности. Надо отметить, что используемые системы измерения, например, СИ и СГС, дают парадоксы, так как не соответствует нормировке количества и закономерностей, которые реальны для мироздания. Например, это приводит к обоснованию на основе этих систем измерения так называемых чёрных дыр, что даёт парадокс невозможности выхода света из гравитационного поля с нарушения закона термодинамического равновесия. Этот парадокс Стивен Хокинг решил за счёт другого парадокса – телепортации. Ещё раз отметим, что придумать иной принцип взаимодействия помимо обмена – невозможно, а обмен обязательно характеризуется скоростью и величиной шага дискретизации. Помимо этого надо отметить, что произведение скорости обмена (света) на шаг дискретизации (постоянная Планка) имеет значение, равное единице, в противном случае либо скорость обмена, либо шаг дискретизации имеют иную величину. Отсюда m0=h=1/с. Таким образом, мы определили значение массы покоя электрона (позитрона) через величину обратно пропорциональную скорости света (обмена) и равную минимальной дискретной величине – постоянной Планка, и тем самым исключили представление массы вне описания через пространство и время. Отметим, что электрон и позитрон сохраняются вплоть до аннигиляции и меньше этих объектов с массой покоя просто быть не может. Соответственно, представление величины объекта зависит от системы наблюдения в иерархии Мироздания при обратно-пропорциональной связи противоположностей, что было нами установлено в виде закона философии [17]. Из сказанного следует, что в качестве массы покоя в одной противоположности выступает скорость обмена в другой противоположности, то есть иными словами, как это будет понятно далее, потенциальная энергия одной противоположности переходит в кинетическую энергию в другой противоположности. Отсюда, следует, что масса покоя электрона характеризует в противоположности величину обменных процессов в объекте со скоростью света, а кинетическая энергия электрона в одной противоположности даёт массу покоя в другой противоположности с учётом обратно пропорциональной связи. Однако, по волновым уравнениям для вектор-потенциалов мы получили зависимость только от массы, в то время как корпускулярно-волновой дуализм требует зависимость и от скорости (скорость также определяет частоту волнового процесса по формуле Луи де Бройля), и это связано с тем, что мы учитывали только сторонний электрический ток по уравнениям Максвелла (31), и не учитывали сторонний магнитный ток, который есть в уравнениях (18). В соответствии с [18], мы используем уравнения Максвелла вида:
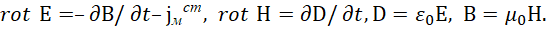(40)
В этом случае магнитные вектор-потенциалы выражают электромагнитные составляющие в виде:
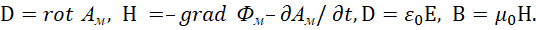(41)
Отсюда получаем связь уравнений стороннего магнитного тока с вектор-потенциалом:
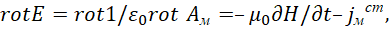
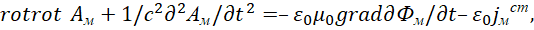
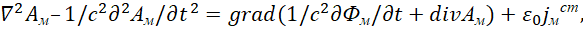
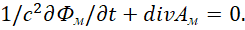(42)
В итоге для магнитных вектор-потенциалов имеем:
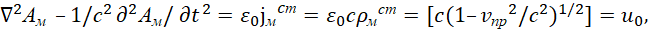
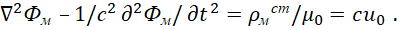(43)
При приведении к одинаковому виду без скорости света получаем зависимость от скорости в противоположности. Таким образом, электромагнитные составляющие в зависимости от системы наблюдения выражаются через преобразования, как в виде массы, так и скорости, а значит, имеют зависимость и от импульса и от скорости. А так как у нас масса и скорость выражаются через глобальные противоположности – длину и время (то есть масса и скорость выражают противоположности в обратно-пропорциональной связи), то мы имеем отражение так называемых зарядов противоположных знаков без чудес. При этом мы имеем взаимосвязь в соответствии с преобразованиями Лоренца-Минковского с взаимным переходом величин, что даёт и притяжение разнородных объектов, и отталкивание однородных объектов. Практически в нашей системе наблюдения электрические и магнитные вектор-потенциалы характеризуют электрические и магнитные нейтрино и антинейтрино, что видно по уравнениям (23) с заменой соответствующих буквенных обозначений. Таким образом, мы получаем полную физическую интерпретацию составляющих в уравнениях Максвелла без чудес. Однако для решения парадокса эффекта Комптона надо связать значения массы и скорости со значением частоты. С этой целью надо показать, как частота электромагнитного сигнала связана с массой и скоростью. В этом случае мы приходим к необходимости математического отображения корпускулярно-волнового дуализма, и он выражается через систему уравнений Дирака на основе закона сохранения энергии по уравнению Эйнштейна в виде:
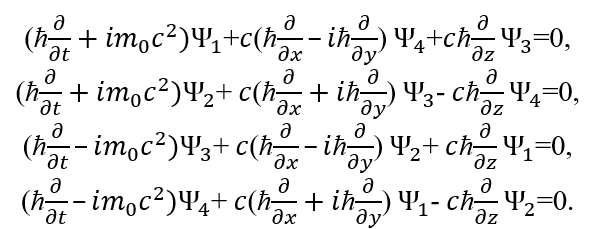(44)
Здесь волновые функции Ψ можно сопоставить с функциями, на основании формул Луи де Бройля с учётом нашей теории. Как мы видим, для описания корпускулярных свойств в системе уравнений Дирака используются уравнения вида:
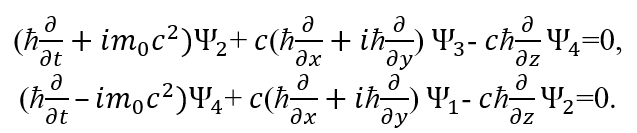(45)
Этот вид уравнений соответствует виду уравнений для электромагнитной волны показанной выше со сторонними токами (23) при замене самих волновых уравнений на источники излучения (поглощения) в соответствии с уравнениями Гельмгольца для уравнения волны и умножении этих источников излучения (поглощения) на мнимую единицу для отображения перехода в противоположность. При значении m0=0, уравнения (45) переходят в уравнения для нейтрино и антинейтрино, что также отмечено в квантовой механике [19], и они по виду полностью соответствуют усовершенствованным уравнениям Максвелла при замене вероятностных волновых функций на электромагнитные, как это было показано нами в [5]. Иными словами, мы убираем чудеса вероятностей, и при этом усовершенствованные уравнения Максвелла описывают реальные объекты. Соответственно два других уравнения, помимо уравнений (45) в системе уравнений Дирака (44) отображают вид усовершенствованных уравнений Максвелла из противоположности в представлении от нашей системы наблюдения с заменой знаков с минуса на плюс, и наоборот. Действительно, если бы вид уравнений сохранялся, то не было бы и взаимодействия, а было бы ассоциативное сложение и вычитание. Собственно переход из одной противоположности в другую со сменой знака сложения на вычитание, и наоборот, это единственный путь обеспечивающий необходимость закономерностей и выполнения закона перехода количества в новое качество. При решении системы уравнений Дирака методом подстановки на основе усовершенствованных уравнений Максвелла мы получаем однозначную связь частоты в аргументе функции Луи де Бройля со значениями скорости и массы при выполнении дифференцирования по переменным, и это обосновывает формулу Луи де Бройля вида: mc2=hf. Собственно показанная нами связь волновых уравнений с зависимостью частоты (длины волны) от величины массы и скорости соответствует и другой формуле Луи де Бройля [20]:
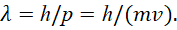(46)
Исходя из того, что на основе усовершенствованных уравнений Максвелла при их взаимодействии, через подстановку одних уравнений в другие, получаются и волновые уравнения, и корпускулярные свойства, на основе уравнения Гамильтона-Якоби, то становится понятно, почему при аннигиляции противоположных частиц образуются фотоны, а при распаде массы электронные и мюонные нейтрино и антинейтрино, так как это связано с образованием из одних и тех же простейших объектов – электронных и мюонных нейтрино и антинейтрино, но при разном сочетании при взаимодействии. Собственно наличие противоположных частиц с притяжением и отталкиванием связано с обменом также электронными и мюонными нейтрино и антинейтрино, так как ничего другого и проще нет. Это полностью убирает необходимость неких гравитонов для описания гравитационного взаимодействия, и гравитацию следует рассматривать как результат электромагнитного взаимодействия, но для противоположных частиц дальнего расположения. А раз проще усовершенствованных уравнений Максвелла без парадоксов ничего придумать невозможно, то дальнейшее развитие науки с описанием практических результатов от простого к сложному варианту может происходить только на основе наших уравнений.
При описании физических процессов мы использовали некие физические величины, отражающие напряжённости электромагнитных полей, значения длин по координатам и время, но надо отметить, что мироздание ничего не знает о наличии наших обозначений, а оперирует лишь закономерностями и количеством. Причём разница между противоположностями отражается через атрибут мнимой единицы, что приводит к смене операции сложения в одной противоположности на вычитание в другой противоположности, и наоборот, и это было показано нами в [17]. Соответственно, стоит также задача показать, каким образом на основе математики, определяющей количественные отношения в соответствии с закономерностями, уже по законам физики получается перераспределение энергии и импульсов в эффекте Комптона, то есть, даёт изменение частоты и импульсов при взаимодействии. Собственно взаимодействие противоположностей на основе корпускулярно-волнового дуализма мы уже показали выше, где мы описали формулы взаимосвязи противоположностей, а отсюда можно говорить о наличии общего пространственно-временного и электромагнитного Континуума. Такой подход позволяет объяснить аннигиляцию электрона и позитрона с образованием фотонов, и наоборот. Отсюда также следует механизм преобразования столь необходимый для объяснения эффекта Комптона, когда фотон одной частоты, сталкиваясь с электроном, имеет изменение направления (что говорит о взаимодействии) и изменение частоты. При этом электрон также имеет новый импульс для движения. Понятно, что особый интерес в практике связан с математическим представлением этого преобразования с соблюдением условия перехода количества в новое качество, чего собственно нет в нынешнем подходе в математике на основе тригонометрических формул преобразования (вид закономерностей сохраняется). То есть, волновые функции синуса и косинуса остаются волновыми и, соответственно, нет перехода к корпускулярным свойствам как к противоположности. В этом случае, например, интерференция электромагнитных волн должна приводить к исчезновению энергии из-за ассоциативного вычитания, и дальнейшее распространение волны было бы невозможно из-за обнуления энергии, что соответствует обнулению электрических и магнитных составляющих. Кроме того, математика допускает отдельное существование корпускулярных и волновых свойств, а в реальности мы имеем именно корпускулярно-волновые объекты. Так как мы рассматриваем вариант существования объектов без распада, то условием существования таких объектов является взаимодействие противоположностей, составляющих объект, через взаимный обмен с условием закона сохранения количества, что соответствует инвариантной форме выведенной в [17]. В этом случае мы имеем общую формулу мироздания:
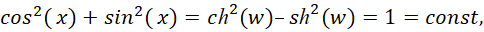
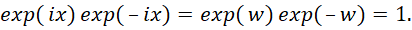(47)
Здесь w=(-1)1/2x. Понятно, что единственный способ это смена знака в противоположностях с выполнением закона перехода количества в новое качество. Другого способа перехода просто нет. При этом переход от одной противоположности к другой связан с заменой системы наблюдения, что выражается через атрибут мнимой единицы с условием соблюдения закона сохранения количества, так как иначе мы бы имели распад объекта. Разница представлений определяется только закономерностями в этих Противоположностях с переходом закономерностей друг в друга (мнимая единица – это атрибут принадлежности к противоположности). Если были бы ещё какие-либо одинаковые закономерности, то о противоположностях не было бы и речи из-за отсутствия их отличий друг от друга. Собственно основа преобразования с соблюдением корпускулярно-волнового дуализма была уже показана через введение Луи де Бройлем его волновых функций. При этом, чтобы оправдать связь массы покоя с частотой, Луи де Бройль постулировал существование волнового поля:
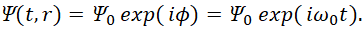(48)
Однако, он не понял, что без противоположной системы наблюдения со сменой пространственно-временного искривления на электромагнитный волновой процесс, это поле будет соответствовать чуду, так как нет его реального воплощения и источника возникновения (именно поэтому учёные и придумали электромагнитный вакуум с виртуальными фотонами, возникающими из ничего). Этот же вопрос касается и волновой функции Луи де Бройля для движущейся частицы со скоростью ν в виде:
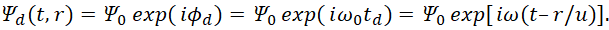(49)
где u=c2/v, ω=ω0γ, γ=1/(1‒v2/c2)1/2. Парадокс здесь связан ещё и с тем, что возникает некая фазовая скорость u=c2/v (можно сравнить с формулой связи вектор-потенциалов А и Ф), которая должна превышать скорость света.
Иными словами, Луи де Бройлю для связи волновых процессов с пространственно-временным искривлением оставалось лишь признать сам переход от преобразований Минковского к волновым функциям, полученным в [15] с соблюдением закона сохранения количества в аргументах:
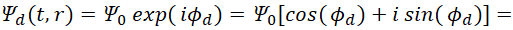
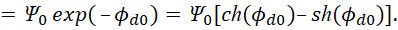(50)
где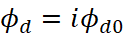 
. Однако, он это сделать не мог, в силу того, что электромагнитные функции в соответствии с классическими уравнениями Максвелла рассматривались как действительные, а не как комплексные функции (не было правила смены функций за счёт смены атрибута принадлежности, что интерпретируется как смена системы наблюдения из одной противоположности на другую). Кроме того, изменения во времени волновой функции никак не связывались со статикой пространственно-временного искривления, и эту проблему в своей геометрии Минковский решил через равенство r = ct, то есть, как бы привёл противоположности в эквивалент одного вида. Фактически Минковский обозначил длину и время как противоположности, изначально связанные через скорость света (скорость обмена). Отсюда статика в одной из них будет выглядеть динамикой движения (изменения) в другой. Следующий шаг по связи противоположностей через мнимую единицу интуитивно сделали в квантовой механике r = ict [7], и это, по сути, означает выполнение закона действия с противодействием, с выполнением разницы между противоположностями, когда сложение в одной противоположности выглядит вычитанием в другой. Таким образом, физики уже сами фактически ввели связь корпускулярных и волновых свойств, и нам оставалось лишь объяснить это логически и дать физическую интерпретацию. Действительно функцию Луи де Бройля, которая соответствует электромагнитной функции, можно записать в виде замкнутой системы в виде:
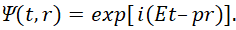(51)
При этом Et–pr=0, что означает неизменный инвариантный вид. С привлечением нашей теории по связи констант, массы покоя, скорости света и постоянной Планка в соответствии с формулой Луи де Бройля [20] (которая может быть выведена из аргумента волновой функции) мы имеем:
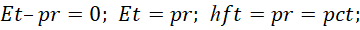(52)
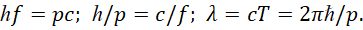
Далее учитываем, что по нашей теории h=m0=1/c; получаем:
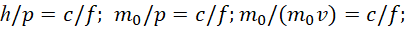
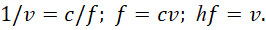(53)
Иными словами, частота и скорость связаны так же как длина и время через скорость света, то есть имеем выражение величин через пространственно-временное искривление, но в противоположности, которые в нашей системе наблюдения выражены через скорость и частоту.
Так как члены, связанные с длиной и временем, являются противоположностями, которые связаны через скорость света, то у нас, для отображения противоположностей в математическом виде, необходимо ввести атрибут противоположности в виде мнимой единицы с условием r=ict. Тогда уравнение (51) можно расписать в виде:
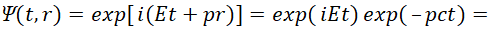
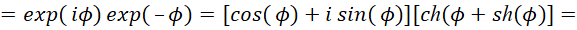
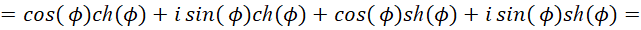(54)
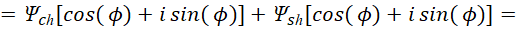
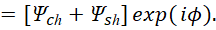
Здесь: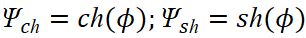 
. По сути, это означает, что мы имеем разложение по величинам длины и времени в соответствии с СТО по геометрии Минковского, выраженных в виде компонент Ψch, Ψsh, которые в противоположности соответствуют волновому представлению в виде волновой функции (48), с частотой Et=ωt. Собственно исходя из того, что количественно по аргументу значения синуса и косинуса имеют соответствие со значениями гиперболического синуса и косинуса, то вариант преобразования (иное означает отсутствие взаимодействия) как раз и будет сопровождаться сложением и вычитанием аргументов функций с изменением частоты. При этом функция Луи де Бройля используется для любых объектов, разница лишь в том, что при взаимодействии в одном случае рассматривается корпускулярная часть, а в другом волновая часть. То есть, виду (54) соответствует любой объект мироздания, как до взаимодействия, так и после взаимодействия, разница лишь в том, что при электромагнитном представлении, величина, выраженная через пространственно-временное искривление, представляется в виде констант электрической и магнитной проницаемости, а при корпускулярном, мы имеем представление с наличием массы покоя с подчинением СТО Эйнштейна, как показано в [21]. Необходимо отметить, что при учёте взаимодействия объекта с внешней средой и сохранении объекта мы будем иметь выполнение общей формулы мироздания (47), которая является неизменной в любой системе координат. При этом соответственно для объекта должно выполняться условие подчинения законам физики обеспечивающих сохранение объекта в динамике на основе усовершенствованных уравнений Максвелла. Это условие выполняется, если для электрической составляющей ввести новые переменные для (47) при отображении динамики взаимодействия через усовершенствованные уравнения Максвелла, например, в виде: 
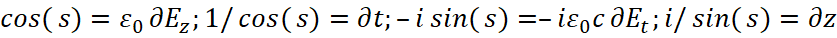, для электрической составляющей, а также представить магнитную составляющую в виде; 
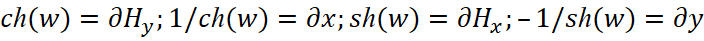. Это можно сделать, так как все функции при дифференцировании дают переход друг в друга с выполнением общей замкнутой формулы мироздания. При этом функция Луи де Бройля для объекта в случае отсутствия распада имеет ответную реакцию в виде функции от внешней среды с обратно пропорциональной связью: 
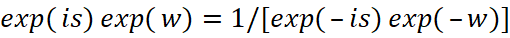. Данный способ замены переменных был сделан не только нами. Аналогичную схему преобразования для уравнения энергии Эйнштейна (а оно также выводится из общего уравнения мироздания) применил и Дирак через «линеаризацию» с заменой импульсов и энергии на дифференциальные операторы. Кроме того, известен подход замены переменных на основе координатного представления (х-представление) и импульсного представления (р-представление) который был показан в квантовой механике [22] в виде:
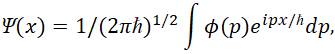(55)
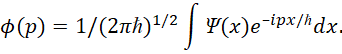
Иными словами, переход от одной системы наблюдения к другой осуществлён через интегрирование, что физически означает взаимосвязь отдельного объекта мироздания со всеми другими объектами мироздания. При этом мы имеем симметричный вид в уравнениях физики от противоположностей, что даёт совпадение законов физики и симметрию с выполнением закона сохранения количества:
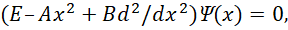(56)
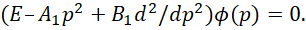
Это означает, что получение значения в координатном представлении по длине (это статика) определяется на основе всех значений от импульсного представления (это динамика), что связано со скоростью и кинетической энергией в противоположности. Повторим, что физически это выражается в том, что мы имеем взаимосвязь каждого объекта мироздания со всеми другими объектами. Это собственно оправдывает наш подход, при котором константы электрической и магнитной проницаемости определяются на основе интегрального усреднённого значения скорости в противоположности. Соответственно в математике известен механизм количественного преобразования используемых функций, который соответствует сохранению формы (54), с использованием известных тригонометрических формул в виде:
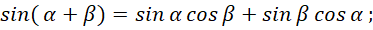
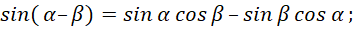(57)
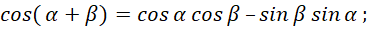
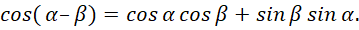
Формулы (57) не рассматривают преобразование противоположностей, а характеризуют только количественное равенство в одной из противоположностей. Как мы установили, электромагнитные составляющие должны иметь комплексный экспоненциальный вид, иначе однозначного преобразования электромагнитных свойств в корпускулярные свойства, не получить. Поэтому, если мы хотим получить экспоненциальный вид, то должны учесть взаимодействие и от мнимой части. Тогда имеем вид:
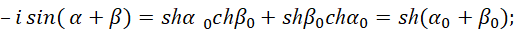
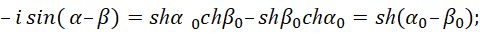
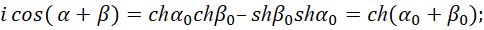
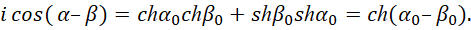(58)
Здесь α=iα0, β=iβ0, ch(α0)=cos(iα0)=cos(α) и sh(α0)=–isin(iα0)=–isin(α).
Соответственно мы имеем вывод, что любое изменение в аргументах функций корпускулярно-волновых объектов, связанное с линейным сложением и вычитанием в волновом виде, даёт нелинейное изменение в пространственно-временном представлении. Иными словами количественное представление в одной противоположности выражается в качественном изменении в другой противоположности.
Отличие нашего подхода от подхода применённого в математике в том, что мы рассматриваем произведение противоположностей, а не закономерностей одного и того же вида. Это связано с тем, что противоположности одного типа не имеют взаимодействия и не могут влиять друг на друга, так как имеют ассоциативное сложение или вычитание. Собственно в математике также выражение суммы или разности аргументов одной закономерности в виде синуса или косинуса не обошлось без представления в противоположностях от значений в двух закономерностях синуса и косинуса одновременно. В соответствии с нашей теорией давать изменение может только одна противоположность, воздействуя на другую, и наоборот. Любой объект Мироздания имеет представление, как в корпускулярном, так и в волновом виде. Причём, для не распадающегося объекта, волновая часть соответствует корпускулярной части в соответствии с законом сохранения количества. Именно это и потребовало описания в виде соответствия волновых свойств и корпускулярных свойств в системе уравнений Дирака. Экспериментально определено, что фотон, сталкиваясь с электроном, изменяет частоту и меняет направление движения. Возвращаясь к рис. 1, видно, что для изменения направления движения фотону необходимо иметь ещё и электромагнитную составляющую с импульсом ортогональным направлению движения к импульсу фотона до столкновения. Собственно данное свойство можно объяснить только на основе аннигиляции противоположностей (в виде зарядов, что пересчитывается в эквивалент длины и времени), которые при аннигиляции дают два фотона противоположной направленности, один из которых поглощён частицей.
То есть, наша теория на основе физики процессов с использованием известных математических формул объясняет как замедление скорости света в плотной среде, так и сам принцип взаимодействия с учётом отражения, преломления, изменения импульса и частоты.
Отсюда следуют выводы:
- Парадокс эффекта Комптона с точки зрения классической электродинамики связан с тем, что описать изменение частоты на основе обычных уравнений Максвелла невозможно в силу ассоциативного сложения и вычитания;
- Парадокс с точки зрения квантовой механики связан с описанием процесса взаимодействия на основе использования сохранении энергии и импульсов, через условие упругого столкновения, которое не имеет физического описания, так как не рассматривается само взаимодействие на основе исходных электромагнитных сил, которые существуют в фотоне. Кроме того, надо представить фотон в корпускулярном виде, а как, если с точки зрения классической электродинамики он имеет только электромагнитное описание?
- Решение парадокса Комптона мы видим в использовании представления объекта через функцию Луи де Бройля, которая в зависимости от системы наблюдения от противоположностей, связанных через скорость света может интерпретироваться через корпускулярный объект на основе преобразований Лоренца-Минковского с эквивалентом массы через пространственно-временное искривление, или как электромагнитный волновой объект с выражением через частоту (корпускулярно-волновой дуализм).
- Изменение направления фотонов и частиц при взаимодействии подчиняется преобразованию корпускулярных свойств в волновые свойства, и наоборот, в соответствии с электрической и магнитной проницаемостью и параметрами движения корпускулярных объектов, характеризующих пространственно-временное искривление на границе раздела между объектами в обеих противоположных системах наблюдения. Причём после взаимодействия первичных объектов, полученные значения частот и пространственно-временных искривлений новых объектов соответствуют функциям Луи де Бройля.
- Условия на границе раздела сред объясняются без парадоксов на основе усовершенствованных уравнений Максвелла без использования неких мифических поверхностных токов и зарядов. Это связано с фактом, что в качестве источников излучения и поглощения использовались конкретные значения констант электрической и магнитной проницаемости.
Таким образом, изменение объектов при столкновении определяется их изначальными значениями с учётом пространственно-временного расположения и направления движения при взаимодействии с окружающей средой на основе пространственно-временного искривления и электромагнитными составляющими. Полученные объекты в условиях отсутствия их распада математически могут описываться на основе системы усовершенствованных уравнений Максвелла по аналогии с системой уравнений Дирака. Физически логика изменения связана с представлением объектов мироздания на основе корпускулярно-волнового дуализма в соответствии с функцией Луи де Бройля с учётом движений в обеих противоположностях с подчинением СТО и ОТО Эйнштейна.
Отметим ещё раз, что при классическом представлении в электродинамике и квантовой механике были использованы математические подгонки под результат с отбрасыванием решений, без учёта преобразований из волнового вида в корпускулярный вид, и наоборот.
.png&w=640&q=75)
