Компетенции по умению пользоваться полученными знаниями в ходе решения различных военно-прикладных задач, приобретенные курсантами в ходе обучения в высшем военном заведении – это один из результатов его обучения. Приоритетом вооруженных сил и системы высшего военного образования является умение вступающих в профессиональную жизнь молодых военных специалистов принимать осознанные решения той или иной задачи, самостоятельно искать выход из встающих перед ними новых проблем. Итог их образования должен «определяться» максимально большим опытом по поиску решения подобных задач.
На наш взгляд необходимо помочь курсантам сформировать «личностное знание», которое должно быть определено самим обучающимся. В этой ситуации роль преподавателя сводится к наставническим функциям – следует научить получать знания, использовать их в профессиональных целях. Прийти к этому можно с помощью проблемных ситуаций, в которые попадает обучающийся при решении практических задач на любой дисциплине. Это в свою очередь должно подтолкнуть обучающегося к поиску возможных решений самостоятельно или в группе. Для того чтобы такой процесс прошёл наиболее плодотворно и формирование «личностного знания» дало наибольший результат необходимо заинтересовать курсанта предметом познания, помочь ему определить мотивы к достижению успеха. Необходимо помнить, что для преподавателя важной составляющей является индивидуализация процесса обучения, учёт особенностей каждого обучаемого в процессе приобретения знаний.
Целесообразнее всего для этих целей использовать такую форму занятий, как практические занятия. Опыт работы в военном вузе показывает, что на практических занятиях вырабатываются не только навыки и умения решения различных задач, но и происходит формирование у курсанта четкого понимания связи приобретенных навыков с будущей практической военно-профессиональной деятельностью. Обучающиеся должны понимать цель такого занятия. Это в свою очередь приводит к осознанию нужности выполняемой работы, её прикладного характера, подтверждает необходимость получения курсантом опыта профессиональной деятельности, демонстрируя связь теории с практикой. Поэтому задача преподавателя состоит в том, чтобы доказать и продемонстрировать курсантам практическую значимость своей дисциплины для решения военно-прикладных задач.
Известно, что в любой сфере профессиональной деятельности, в том числе и военной, приходится иметь дело с большими объёмами информации, как текстовой, так и числовой, представленной в табличной форме. Чаще всего необходимо не просто обработать эту информацию, а выполнить расчёты. Наиболее удобным средством работы с документами, имеющими табличную структуру, является программа Microsoft Excel. Сегодня электронные таблицы нашли широкое применение не только в экономических и бухгалтерских расчетах, но для решения задач специального назначения, а именно – военно-прикладных.
Такого рода задачи становятся всё более наполненными сложными математическими вычислениями, для выполнения которых возможностей Microsoft Excel бывает недостаточно. Вычисления скалярных, матричных и векторных величин, расчет дифференциальных уравнений, поиск корней многочленов, решение систем уравнений. Возможность сопровождать это графической визуализацией в 2D и 3D, в зависимости от решаемой функции. Составление как линейных, так и циклических программ. Все эти возможности предоставляет, в частности, математическая система Mathcad, которая нашла свое применение и при решении некоторых военных задач.
Рассмотрим решения некоторых типично военно-прикладных задач с помощью табличного процессора Microsoft Excel и системы Mathcad. Одной из таких задач является задача на определение корреляционной и регрессионной зависимости между двумя признаками выборочной совокупности большого объема. Курсантам поясняется, что корреляционный анализ помогает установить, есть ли между показателями в одной или двух выборках связь. Обычно преподавателями приводятся примеры: между временем работы прибора и стоимостью его обслуживания, ценой техники и продолжительностью эксплуатации, ростом и весом военнослужащего и т.д. Если связь имеется, то влечет ли увеличение одного параметра повышение (положительная корреляция) либо уменьшение (отрицательная) другого. Корреляционный анализ помогает аналитику определиться, можно ли по величине одного показателя предсказать возможное значение другого [1].
Одной из задач военно-прикладной направленности является задача следующего содержания: при приготовлении дегазирующего раствора заданной концентрации были получены следующие данные, представленные в таблице, где Х – температура раствора, (0С), Y – масса извлеченного вещества, (мг).
Таблица
Исходные данные задачи
|
X |
40 |
40 |
40 |
40 |
40 |
60 |
60 |
60 |
60 |
60 |
60 |
80 |
80 |
80 |
80 |
80 |
80 |
80 |
100 |
100 |
|
Y |
60 |
60 |
60 |
60 |
80 |
60 |
80 |
80 |
100 |
100 |
80 |
80 |
80 |
100 |
100 |
120 |
80 |
120 |
100 |
100 |
Для выполнения корреляционного анализа требуется:
- построить корреляционную таблицу;
- найти выборочный коэффициент корреляции и проверить его значимость;
- составить уравнение прямой регрессии Y на X;
- построить диаграмму рассеивания и график прямой регрессии.
Задача решается разными прикладными программами. Рассмотрим методику решения в приложении Microsoft Excel [2]. Обучаемые руководствуются следующим планом:
1. Составляется корреляционная таблица.
A) на листе 1 в столбец А таблицы вводятся исходные данные значения Х, в столбец В таблицы вводятся исходные данные значения Y задачи рассматриваемого варианта (рис.1).
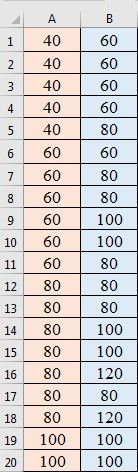
Рис. 1. Исходные данные задачи
В) копируются все данные столбца А в столбец D;
С) выделяются все данные столбца D;
D) во вкладке «Данные» в группе «Работа с данными» выбирается команда «Удалить дубликаты»;
E) копируются все данные столбца B в столбец E;
F) выделяются все данные столбца E;
G) во вкладке «Данные» в группе «Работа с данными» выбирается команда «Удалить дубликаты» (рис. 2);
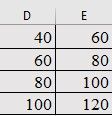
Рис. 2. Данные для составления корреляционной таблицы
H) в блоке ячеек G1:L6 разрабатывается таблица по образцу, представленному на рисунке 3, где в строке заголовка – значения X (столбец D), в столбце заголовка – значения Y (столбец Е).
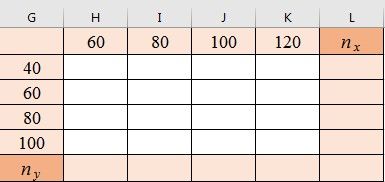
Рис. 3. Таблица для расчетов
I) таблица заполняется формулами вычисления количества значений, удовлетворяющих заданному условию:
- в ячейку H2 вводится формула:
=СЧЁТЕСЛИМН($A$1:$A$20;$G2;$B$1:$B$20;H1);
- формула копируется в ячейки I2:K2;
- в ячейку H3 вводится формула:
=СЧЁТЕСЛИМН($A$1:$A$20;$G3;$B$1:$B$50;H1);
- формула копируется в ячейки I3:K3;
- действия повторяются в оставшихся ячейках таблицы;
- в ячейку H6 вводится формула:
=СУММ(H2:H5);
- формула копируется в ячейки I6:K6.
Результат представлен на рисунке 4.
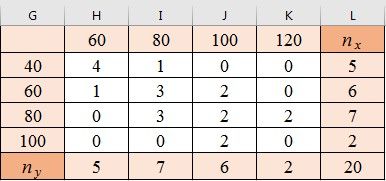
Рис. 4. Корреляционная таблица
2. Выборочный коэффициент корреляции определяется по значениям составленной корреляционной таблицы, представленной на рисунке 4, с использованием формул (1)-(9):
a) Определяются несмещенные выборочные характеристики 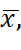
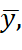 Sy, Sx.
Sy, Sx.
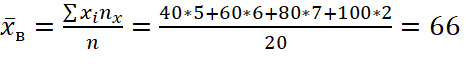 (1)
(1)
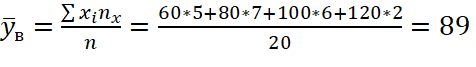 (2)
(2)
Выборочные дисперсии:
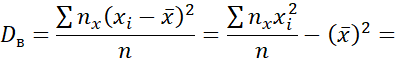
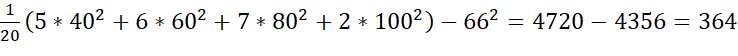 (3)
(3)
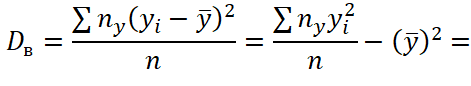
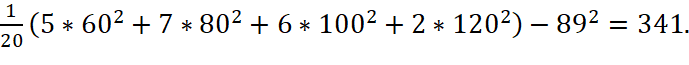 (4)
(4)
Исправленные дисперсии:
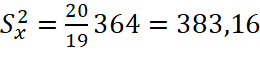 (5)
(5)
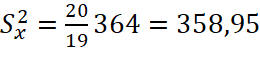 (6)
(6)
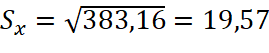 (7)
(7)
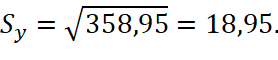 (8)
(8)
b) Определяется выборочный коэффициент корреляции:
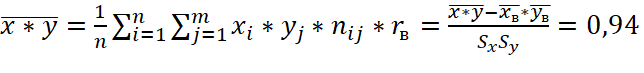 (9)
(9)
3. Составляется уравнение прямой регрессии по формуле (10) и по данным, полученным в п.2:
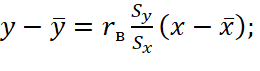 (10)
(10)
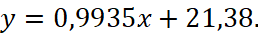
4. По данным исходной таблицы (рис.1) строится диаграмма рассеивания (рис. 5) и график по уравнению прямой регрессии, полученному в п.3. (рис.6) и делается вывод, что между показателями в выборках существует связь.
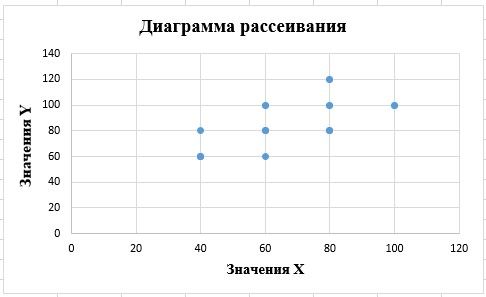
Рис. 5. Диаграмма рассеивания
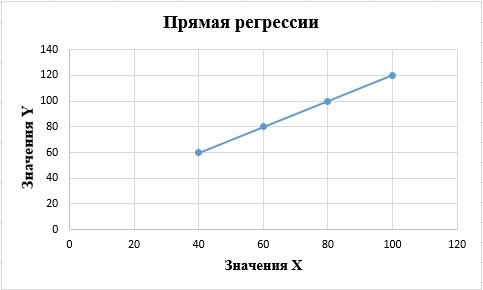
Рис. 6. Прямая регрессии
Таким образом, в статье рассмотрены алгоритмы решения стохастических задач средствами табличного редактора Excel, которые показывают, что использование информационных технологий значительно увеличивает скорость расчётов и позволяет добиваться высоких результатов при решении прикладных военно-инженерных задач. Помимо всего прочего поиск ответов на поставленные в таких задачах проблемы приводит к устойчивому формированию у курсантов понимания связи приобретенных навыков при освоении дисциплины «Информатика» с будущей практической военно-профессиональной деятельностью.

.png&w=640&q=75)