Сингулярное разложение – это разложение прямоугольной вещественной или комплексной матрицы в виде [1]
𝐴 = 𝑈Σ𝑉𝑇. (1)
Схематически
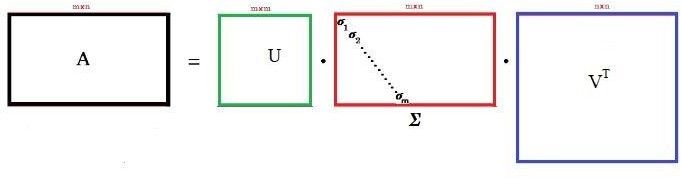
Рис. 1
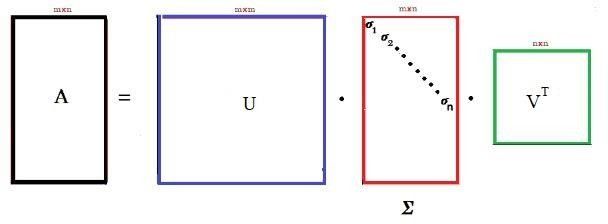
Рис. 2
В (1) матрицы 𝑈 и 𝑉 являются ортогональными, при этом матрица 𝑈 называется левой сингулярной, а матрица 𝑉 – правой сингулярной. Столбцы матрицы 𝑈 являются собственными векторами матрицы 𝐴𝐴𝑇; столбцы матрицы 𝑉 являются собственными векторами матрицы 𝐴𝑇𝐴. Матрица Σ – диагональная матрица: Σ = diag(𝜎1, 𝜎2, … , 𝜎𝑘, 0,0, … ,0). Числа 𝜎𝑖 (𝑖 = ̅1̅̅,̅𝑘̅) называются сингулярными числами матрицы 𝐴 и нумеруются в порядке убывания. Отметим, что квадраты сингулярных чисел 𝜎𝑖 (𝑖 = ̅1̅̅ ,̅𝑘̅) матрицы 𝐴 совпадают с собственными значениями матрицы 𝐴𝑇𝐴, а число k ненулевых значений сингулярных чисел равно рангу матрицы 𝐴 [2].
Сжатие изображений методом SVD
С помощью SVD можно реализовать фильтрацию и сжатие данных, которые задаются в виде матрицы. Рассмотрим пиксельное изображение якоря на рисунке 3. В каждой ячейке число означает уровень интенсивностицвета (от 0 до 1).
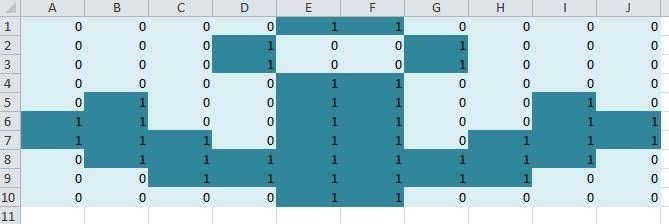
Рис. 3

Найдем сингулярное разложение матрицы 𝐴:
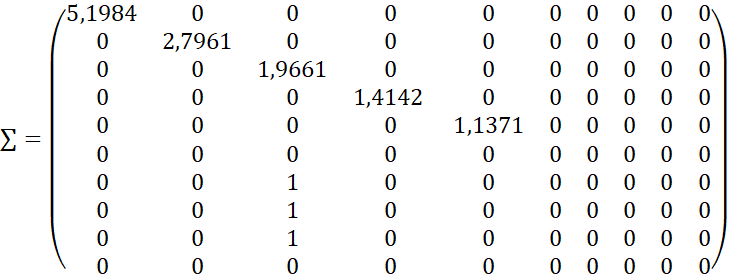
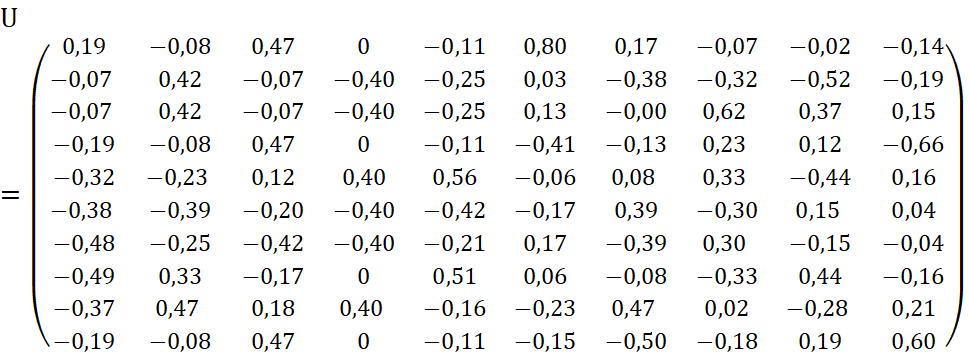
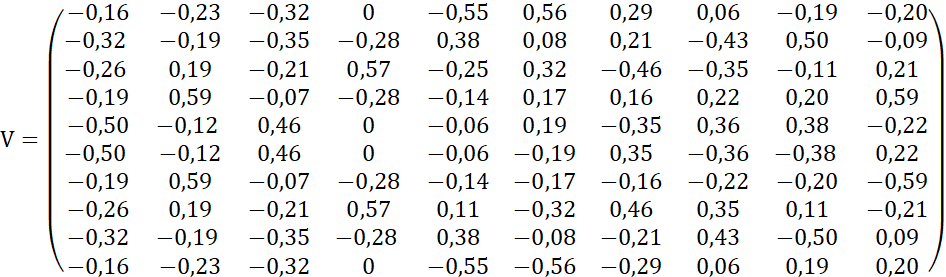
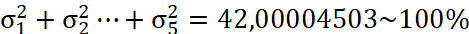
Из матрицы сингулярных чисел Σ отбрасываем те строки и столбцы, которые оказались меньше некоторого априорно заданного порога ε.
Возьмем ε = 2, тогда:
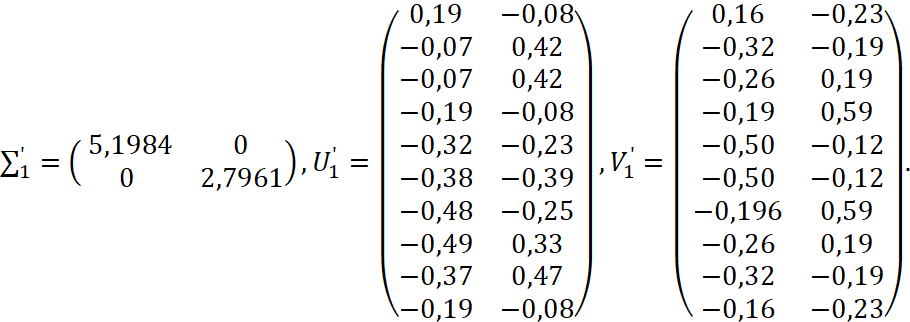
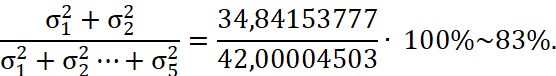
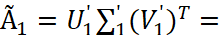
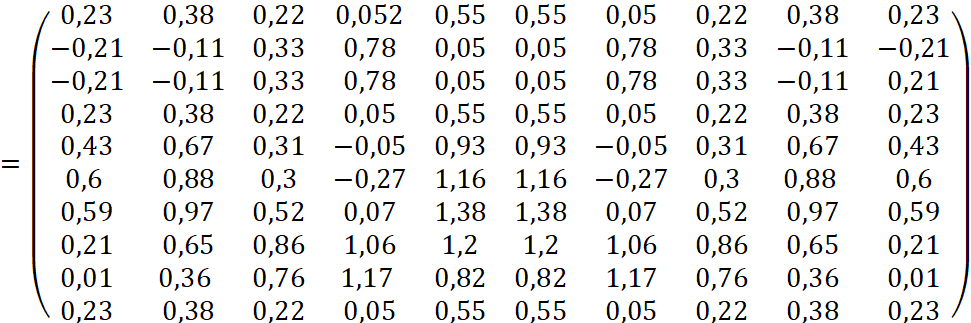
На рисунке 4 представлено изображение после фильтрации при отбрасывании сингулярных чисел меньше ε = 2.
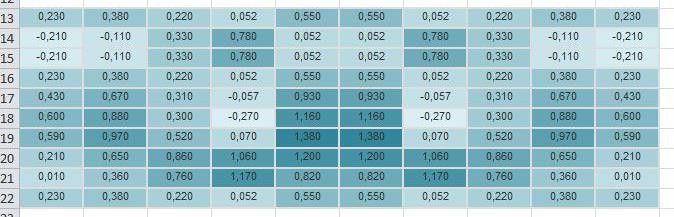
Рис. 4. Потеря данных примерно 17%
Теперь из матрицы сингулярных чисел Σ отбросим те строки и столбцы, которые оказались меньше ε = 1,5:
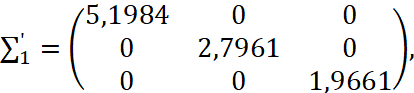
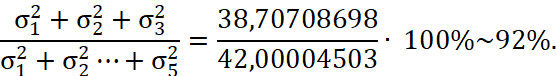
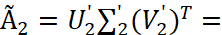
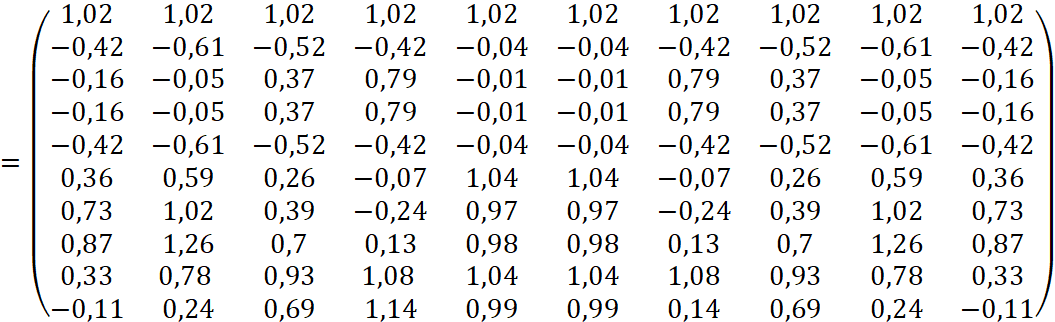
На рисунке 5 представлено изображение после фильтрации при отбрасывании сингулярных чисел меньше ε = 1,5.
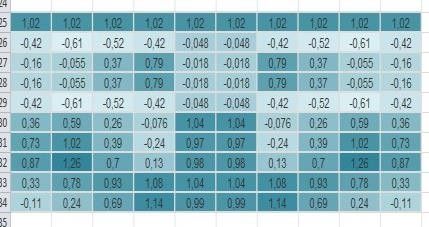
Рис. 5. Потеря данных примерно 8%
Математика – одна из важнейших наук, основанная на выполнении конкретных целей и задач. Она является главной составляющей многих сфер жизни общества. Политика, физика, медицина, информатика, экономика – все это не может существовать без математики. Любая информация подвержена обработке, а поэтому метод сингулярного разложения матриц очень ценен в мире, где большее предпочтение отдается компьютеру.

.png&w=640&q=75)