Пересмотр специальной теории относительности

Предисловие

Конец 19-го века и начало 20-го ознаменовались для физики бурным развитием: была открыта радиоактивность, выяснилось, что «неделимый» атом имеет сложную структуру, открыты кванты света и вещества и т.д. Список этот можно продолжить, но уже названного достаточно, чтобы понять, что физиков просто захлестнула лавина проблем, требующих своего разрешения и объяснения. И они их решали. Но не всегда удавалось найти решение, полностью закрывающее проблему. В таких случаях находили временное решение, выводящее из тупика на данный момент. Потом нередко к этому временному привыкали, и оно начинало восприниматься как постоянное. При этом казалось, что человечество вышло на такой уровень познания, когда невозможно построить наглядные модели новых открытых явлений. Не случайно Нильс Бор однажды заметил: «Вам никогда не понять квантовой физики, к ней можно только привыкнуть» [4, с.117]. Ему же приписывают характерное для того времени высказывание в ответ на просьбу одного из своих учеников оценить его новую идею, которой он поделился со своим мэтром. Мэтр его огорчил, сказав, что идея недостаточна безумна, чтобы быть верной. При таком настрое некоторые временные и прямо-таки экзотические решения постепенно перешли в разряд постоянных и чуть ли не классических. В их верности уже никто (за редчайшим исключением) не сомневается.

К таким временным решениям автор относит, в частности, теории относительности Эйнштейна: специальную и общую. Здесь речь будет идти о первой. Что касается общей теории относительности автор этих строк выразил своё отношение к ней в статье «Теория гравитации на основе модели Лесажа» [8, с. 7-8]. Коротко говоря, оно состоит в согласии с её оценкой известным французским физиком Леоном Бриллюэном, который охарактеризовал её как «блестящий пример великолепной математической теории, построенной на песке и ведущей ко всё большему нагромождению математики в космологии (типичный пример научной фантастики)» [1, с. 28].

Однако знания, накопленные за прошедший век, позволяют по-новому взглянуть на такие надолго задержавшиеся временные решения и внести необходимые коррективы.

Введение

Создание специальной теории относительности было вызвано необходимостью объяснить результаты экспериментов по выявлению движения Земли относительно эфира. Первый раз эти опыты провёл А. Майкельсон на построенном им интерферометре в 1881 году. Однако результат опыта оказался отрицательным. Чтобы не сомневаться, Майкельсон решил повторить эксперимент. На этот раз он действовал совместно с Э. Морли, причём они сначала усовершенствовали прибор, повысив его чувствительность [2, с. 198-199  Но и на этот раз никакого относительного движения обнаружить не удалось.

Материалы этих экспериментов были проанализированы Г. Лоренцем. Он пришёл к выводу, что их отрицательный результат можно объяснить сокращением длины в направлении движения Земли в отношении: 1: ,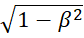

где 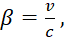  v – скорость движущейся системы отсчёта относительно неподвижной (в данном случае - скорость движения Земли), c – скорость света.

Как выяснилось позже, такое же сокращение было предложено Фицджеральдом, поэтому его стали называть сокращением Лоренца – Фицджеральда. А в 1904 году Лоренц написал уравнения связи между координатами рассматриваемого тела (частицы) в движущейся и неподвижной системах отсчёта. Такие же уравнения ранее (в 1900 году) написал Д. Лармор, причём именно в том виде, в котором они в наше время употребляются в специальной теории относительности и называются преобразованиями Лоренца. Приводим эти уравнения в виде выражений координат и времени в неподвижной системе через координаты и время в подвижной системе [9, с. 231]:

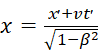,  y = y׳, z = z',  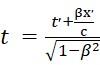   (1)

Штрихами помечены координаты в движущейся системе. При этом предполагается, что соответствующие оси координат систем параллельны, а движение со скоростью v происходит вдоль оси абсцисс (x).

Эйнштейн уравнения связи между координатами в движущейся и неподвижной системах впервые выводит в 1905 году (Лармор их постулировал). При этом у него «во главу угла ставится принцип относительности и принцип постоянства скорости света» [2, с. 210].

Штрихами помечены координаты в движущейся системе. При этом предполагается, что соответствующие оси координат систем параллельны, а движение со скоростью v происходит вдоль оси абсцисс (x).

Эйнштейн уравнения связи между координатами в движущейся и неподвижной системах впервые выводит в 1905 году (Лармор их постулировал). При этом у него «во главу угла ставится принцип относительности и принцип постоянства скорости света» [2, с. 210].

Из этих преобразований вытекают важные следствия, которых не знала классическая физика [9, с. 232-234]. Первое – это сокращение Лоренца – Фицджеральда, о котором упоминалось выше. В соответствии с ним, если в покоящейся системе расположен в направлении оси x стержень, имеющий длину l = x₂ – x₁, то в движущейся вдоль оси x со скоростью v системе длина этого стержня l֓ будет меньше и равна:

.

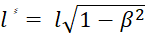Второе следствие – длительность события в движущейся системе больше длительности такого же события в неподвижной системе:

t׳₂ – t₁׳ = .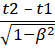

Наконец, следствием преобразований (1) является также новая формула сложения скоростей, в проекциях на оси координат она имеет следующий вид:

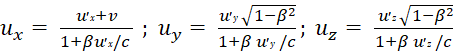.     (2)

Если частица (точечное тело) движется параллельно осям x и x׳ в направлении скорости v, то u_x совпадает с модулем u, а  – с модулем u׳. В результате получается:

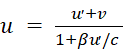.     (3)

Согласно (3), если каждая из складываемых скоростей не превышает c, то и результирующая скорость не может превысить величину c.

Кроме того, «чтобы в механике теории относительности, как и в механике Ньютона, для изолированной системы тел выполнялся в любой системе закон сохранения количества движения и учёт законов преобразования скоростей при переходе из одной системы в другую, приводит к выводу, что масса тела должна иметь разные значения в разных системах, находящихся в относительном движении. Закон преобразования масс при этом окажется следующим:

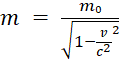     (4)

Здесь m₀ есть значение массы, измеренной в системе, в которой она покоится, а m – значение той же массы, измеренной в системе, движущейся относительно первой с постоянной скоростью v» [9, с. 241-242].

При использовании значения массы из (4) в уравнении движения стал возможным вывод формулы связи между энергией и массой [9, с. 242-244]:

E = m c².    (5)

Формулы (4) и (5) сыграли большую роль в утверждении специальной теории относительности как экспериментально подтверждённой теории. Но, как будет показано далее, это явилось результатом их некорректного толкования. В первую очередь, это относится к формуле (4).

Обоснование ненужности преобразований Лоренца

Основы специальной теории относительности Эйнштейн изложил в статье «К электродинамике движущихся сред», опубликованной в 1905 году. Так что проблема отрицательных результатов экспериментов по определению скорости движения Земли относительно эфира была решена. Но какою ценой! Отмеченные выше следствия новой теории выглядели очень необычно. Так что совсем не удивительно, что полного признания теория Эйнштейна не получила. «И когда в 1921 году Альберту Эйнштейну присудили Нобелевскую премию по физике, то сделали это не за самую знаменитую его идею – теорию относительности. Премию присудили за работу по фотоэлектрическому эффекту» [4, с. 53].

Но с течением времени в соответствии с приведенным в предисловии замечанием Нильса Бора к новой теории попривыкли, и сомневающихся в ней почти не осталось. В то же время этого нельзя сказать об общей теории относительности, созданной несколько позже (примерно к 1914 г. [2, с. 209]). К этой теории относятся по-разному: кто-то как к едва ли не красивейшей физической теории, а кто-то считает, что она ничего не дала для практической физики. А её строгий критик Леон Бриллюэн даже противопоставляет общей теории относительности специальную, называя последнюю фундаментальным открытием [1, с. 28-29]. Ещё конкретнее высказался по этому поводу в предисловии редактора перевода к данной работе академик АН УССР Петров А. З., который отметил «великолепное подтверждение специальной (частной) теории относительности в ядерной физике и, к сожалению, совершенно недостаточное опытное подтверждение общей теории относительности.» [1, с. 8]. При этом он, отмечая великолепное подтверждение, безусловно, имел в виду формулы зависимости массы от скорости (4) и связи энергии и массы (5). Действительно, эти формулы успешно применяются в ядерной физике и сыграли большую роль в утверждении специальной теории относительности как экспериментально подтверждённой теории. Но, как уже было отмечено выше, это явилось результатом их некорректного толкования.

Принцип относительности Галилея заключается в том, что «никакими механическими опытами, проделанными в пределах данной системы отсчёта, нельзя установить, находится ли она в состоянии покоя или в состоянии равномерного и прямолинейного движения» [5, с 68]. Отрицательный результат экспериментов Майкельсона и Морли показал, что принцип относительности можно распространить и на электромагнитные явления, в том числе и оптические, являющиеся их частным случаем. Что и было сделано Эйнштейном. По сути это и было объяснением отрицательного результата рассматриваемых экспериментов. Ведь интерферометр находился в системе, неподвижной относительно Земли, и наблюдавшиеся с его помощью оптические процессы также происходили в пределах этой системы.

Казалось бы, на этом можно было остановиться и не искать каких-то новых преобразований. Но как быть с формулами (4) и (5), имеющими вроде бы хорошее согласие с экспериментальными данными? Разберёмся с этим.

Ещё в далёком от нас 1908 году Г. Льюисом был предложен вывод зависимости массы от скорости, не основывающийся на преобразованиях Лоренца. Он приведен в учебном пособии по физике [3, с. 394-395] К. Путиловым. Учитывая важность этого вывода для понимания излагаемых здесь вопросов и то, что учебное пособие [3] сейчас уже библиографическая редкость, приводим его здесь. При этом, чтобы избежать путаницы в понятиях, обозначение скорости частицы изменяем с буквы v на букву u, которой в теории относительности принято обозначать скорость частицы в неподвижной системе отсчёта, что подразумевается в данном выводе.

Пусть частица с массой m под действием силы F = d(m u)/dt получает на пути ds вследствие ускорения приращение кинетической энергии E:

.

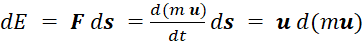По закону пропорциональности массы и энергии прирост кинетической энергии должен повлечь за собой пропорциональное увеличение массы частицы:

dE = c² dm.

Из этих двух уравнений получаем:

c² dm= u d(mu)= u² dm + m u du.

Отсюда после несложных преобразований получаем:

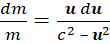.    (6)

Интегрируя последнее уравнение от u = 0 до u и соответственно от m₀ до m, после простых преобразований получаем искомое выражение зависимости массы от скорости:

m = 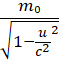.     (7)

Ещё раз подчеркнём, что приведенный вывод произведен при рассмотрении движения с ускорением и не имеет никакого отношения к преобразованиям Лоренца. Полученная формула и формула (4), внешне выглядят одинаково, но смысл они имеют разный. Формула (7) – это результат разгона частицы, покоившейся в неподвижной системе отсчёта, до скорости u путём передачи ей массы движения и тем самым увеличивая полную массу частицы, а формула (4) – это результат измерения данной массы покоя m₀ в движущейся системе измерения (как такое измерение производится не оговаривается, зато ясно, что реального изменения массы не происходит). При внешней похожести в этих формулах используются значения скорости разных объектов. В (4) – это скорость движущейся системы относительно неподвижной, а в (7) – это скорость частицы относительно неподвижной системы. Экспериментом подтверждается, конечно, формула (7), а не (4).

Казалось бы, вывод Льюисом формулы (7) должен был коренным образом повлиять на решение вопросов теории относительности, но этого почему-то не произошло. Видимо, это связано с тем, что в данном выводе используется закон пропорциональности массы и энергии E = m c², а он получался с использованием преобразований Лоренца [9, с. 243-244]. Но сейчас этот закон, как будет показано дальше, может быть выведен без всякой связи с преобразованиями Лоренца.

Кроме того, могла сыграть свою роль почти полная внешняя идентичность формул (4) и (7), и вывод Льюиса был воспринят как новый вариант вывода той же формулы. Эта версия подтверждается тем, что даже значительно позже Путилов, приводя в [3] вывод Льюиса, отмечал только методический и методологический интерес этого вывода. И только в начале 21-го века в пятом издании Курса общей физики Савельева И. В. [5] было обращено внимание на то, что в формуле (4) что-то не так. Возможно, наконец, обратили внимание на то, что в этой формуле фигурирует не скорость частицы, которую замеряют в эксперименте, а скорость движущейся системы координат. Во всяком случае, по поводу формулы (4) на стр. 222 была дана сноска: «Так называемую релятивистскую массу (т. е. массу, зависящую от скорости) мы не рассматриваем. Понятие релятивистской массы не адекватно существу теории относительности и только затуманивает смысл этой теории.».

Таким образом, для вывода формулы (7) зависимости массы от скорости, имеющей убедительное экспериментальное подтверждение, не требуются преобразования Лоренца. Покажем, что они не требуются и для вывода закона пропорциональности массы и энергии.

В настоящее время нам известны массы двух видов: масса покоя и масса движения. Первую из них будем обозначать как m₀, а вторую как m_c. Индекс второй как бы служит напоминанием, что масса движения всегда имеет скорость c. В классической механике всегда имеют дело только с массой покоя. Но современная физика имеет дело и с объектами, имеющими только массу движения, в качестве примера в первую очередь вспоминаются кванты света – фотоны. Сейчас нам известно, что частицы, имеющие массу покоя, могут превращаться в частицы, имеющие массу движения. Так при аннигиляции, например, при столкновении электрона с позитроном эти частицы превращаются в кванты ϒ – фотонов. Происходят и обратные процессы рождения пар частиц, имеющих массу покоя [6, с. 330-331]. Есть и частицы с массой покоя, но движущиеся с высокими скоростями, например, тот же электрон, разогнанный в ускорителе до высоких скоростей, сопоставимых со скоростью света; при этом он увеличивает свою массу в соответствии с (7). В этом случае частица имеет и массу движения, и массу покоя, а её полная масса равна их сумме:

m = m₀ + m_c.    (8)

При этом полная масса является инвариантом и не меняется при переходе из одной инерциальной системы в другую. Это можно рассматривать как следствие закона сохранения массы – масса не может исчезать и возникать из ничего, она может только переходить из одной формы в другую.

Рассмотрим уравнение движения тела в классической механике (второй закон Ньютона), в котором сила F приравнивается производной по времени количества движения p = m v, и уравнение движения имеет вид:

.

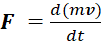По правилам дифференцирования имеем: d(mv) = dm v + m dv.

Учитывая (8), получаем: d(mv) = d(m₀ + m_c) v + (m₀ + m_c) dv.

Классическая механика применяется только когда скорости рассматриваемых тел пренебрежимо малы по сравнению со скоростью света и соответственно так же мала масса движения по сравнению с массой покоя, на основании чего полагается, что m_c ≈ 0 и m ≈ m₀ ≈ const. В результате уравнение движения имеет вид: F = m dv/dt.

А при рассмотрении частиц, имеющих только массу движения, константой является скорость v = c, её производная равна нулю, а количество движения изменяется за счёт изменения массы. Поэтому уравнение движения получает вид: F = c dm_c /dt = c dm /dt. Интересующая нас здесь величина энергии E – это величина, изменение которой равно работе A. Дифференциал работы равен dA = F ds = c dm ds/dt = c² dm. Интегрируя полученное выражение от 0 до m, имеем: A= E(m) – E(0) = c² m, то есть, учитывая, что E(0) = 0, получаем искомую формулу E = m c². Правда, она выведена только для частиц с массой движения. Но поскольку имеет место взаимопревращение массы движения в массу покоя и наоборот, естественно распространить эту формулу и на случай масс покоя. Таким образом, отпадает ещё один аргумент в пользу необходимости преобразований Лоренца.

В результате изложенного выше получается, что специальная теория относительности не имеет приписываемых ей серьёзных экспериментальных подтверждений – вместо формулы (4) такие подтверждения имеет формула (7), не имеющая отношения к преобразованиям Лоренца, являющимся основой теории относительности. Не имеет к ним отношения и приведенный выше вывод формулы (5).

Кроме всего уже сказанного не в пользу преобразований Лоренца хочется обратить внимание ещё на один аспект. Покажем его на примере парадокса близнецов, который выводят из рассмотренного здесь ранее второго следствия преобразований Лоренца, состоящего в том, что длительность событий в движущейся системе больше длительности такого же события в неподвижной системе. Поясним, что это такое, на примере из [7, с. 687].

«Из двух братьев-близнецов A остаётся на Земле, а B отправляется в кругосветное путешествие на межзвёздном корабле, двигаясь со скоростью, близкой к скорости света. Через 5 лет по своим часам он возвращается обратно и находит брата A глубоким стариком. Оказалось, что за время путешествия по часам на Земле прошло 50 лет. Таким образом, открывается возможность за время человеческой жизни совершать не только путешествия к далёким звёздным мирам, но и путешествие в будущее». Первое, что хочется сказать по этому поводу – прекрасный подарок для фантастов!

Однако, если внимательнее вникнуть в механизм этого парадокса, то выясняется его несостоятельность. Ведь все инерциальные системы равноправны, и неподвижной мы принимаем какую-то из них условно для удобства решения конкретной задачи. Поэтому эффекты изменения длины и промежутка времени взаимны и имеют место не в той системе, где находится рассматриваемый объект, а в другой инерциальной системе, т.е. по существу это не реальные, а кажущиеся изменения.

Здесь напрашивается аналогия со всем известным эффектом перспективы – видимым уменьшением размеров предметов при их удалении. Так, два путника, идущие навстречу друг другу по ровной дороге, уже на расстоянии около километра (а при хорошем зрении – и больше) видят друг друга. При этом вначале они кажутся друг другу очень маленькими, но по мере приближения выглядят всё крупнее и крупнее. А при встрече предстают друг перед другом уже в натуральную величину. И в этом отношении картина принципиально не меняется, если один из путников будет стоять на месте.

Так же и с близнецами в упомянутом парадоксе. Хотя улетает близнец B, но и близнец A относительно него движется. Да, при отлёте и возвращении имеет место ускорение и торможение, этим B отличается от A, но предполагается, что это занимает относительно небольшую часть времени, а большая часть проходит в равномерном движении - иначе нельзя было бы применять зависимости специальной теории относительности. Так что большую часть времени близнецы находились в состоянии равномерного движения относительно друг друга и эффект сокращения времени был бы для обоих близнецов. Из этого следует, что он мог быть только кажущимся.

Таким образом, в пользу необходимости преобразований Лоренца остаются только формулы сложения скоростей (2) и (3), обеспечивающие выполнение требования не превышения значения скорости света c при сложении скоростей, каждая из которых не больше c. Однако, аналогичные формулы можно получить и без привлечения преобразований Лоренца. Покажем это.

Вывод новых преобразований скоростей

Итак, мы пришли к тому, что преобразования Лоренца не нужны как не имеющие экспериментального подтверждения. А что же вместо них? Да просто преобразования Галилея из механики Ньютона [5, с.66]:

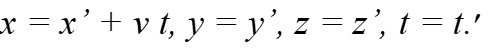 (9)

Они даны здесь в предположении, что соответствующие оси координат обеих систем параллельны, а скорость подвижной системы v направлена вдоль оси абсцисс. В математическом отношении это простейший случай, при котором легче выявляется физическая сущность рассматриваемого явления, поскольку не приходится отвлекаться на математические сложности, возникающие в других случаях. Поэтому здесь мы пока этим случаем и ограничимся.

Что нового возникает при рассмотрении движения тел со скоростями, сопоставимыми со скоростью света? Из явлений, надёжно подтверждённых экспериментально, это зависимость массы тела от его скорости (7) и формула связи между энергией и массой (5). А из специальной теории относительности Эйнштейна остаются в силе положенные им в основание своей теории принципы относительности и постоянства скорости света в вакууме. Учёт этих обстоятельств никак не влияет на вид преобразований координат Галилея (9). Но со скоростями дела обстоят сложнее. Разберёмся с этим.

Из формулы (7) выразим значение скорости частицы:

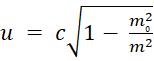.     (10)

Из этой формулы видно, что скорость точечного тела (частицы) не может превысить скорость света в вакууме с. Действительно, полная масса частицы m равна сумме массы покоя m_₀ и массы движения m_c. Отсюда следует, что величина квадратного корня из (10) всегда меньше единицы, точнее не больше (при m₀= 0 будет u = c), что и обеспечивает заявленное неравенство. Но это ещё не обеспечивает не превышения величины скорости света суммой скоростей. Ведь в механике Ньютона сумма скоростей формулируется довольно просто: скорость u точечного тела в системе координат, которая считается неподвижной, равна векторной сумме его скорости u׳ в подвижной системе и скорости v подвижной системы относительно неподвижной [5, с. 67]:

u = u׳ + v.     (11)

Из этой формулы видно, что достаточно в правой части равенства иметь, например, одно из слагаемых равным половине скорости света, а второе при этом – хотя бы немного большим её половины, и величина их суммы превысит значение скорости света. Выходит, что вместо (11) необходимо вывести новую формулу сложения скоростей, обеспечивающую не превышение величины скорости света суммой скоростей. Для достижения этой цели выведем зависимости между скоростями частиц в неподвижной и движущейся системах отсчёта.

Пусть скорость рассматриваемой частицы и её масса покоя в неподвижной системе равны соответственно u и m₀, а скорость движущейся системы относительно неподвижной равна v (как было оговорено выше, вдоль оси x неподвижной системы). Полную массу вычисляем по (7). Наша задача сейчас определить, какие параметры будет иметь рассматриваемая частица в движущейся системе. При этом возможны различные варианты в зависимости от соотношения значений скоростей u и v.

Самый простой случай, когда u = v. Очевидно, что при этом скорость частицы в движущейся системе равна нулю (u’= 0), т.е. частица неподвижна. А отсюда следует, что в этой системе масса покоя частицы m₀’ равна её полной массе m’, которая в свою очередь равна полной массе частицы в неподвижной системе (вследствие инвариантности полной массы). В результате, учитывая, что u = v, имеем:

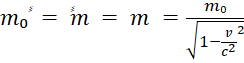.     (12)

Далее рассмотрим случай, когда u> v. В этом случае частица в движущейся системе отсчёта будет иметь какую-то скорость u’. Выражение для полной массы частицы в этой системе имеет вид:

m֓  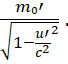=      (13)

Но как мы видели выше, в движущейся системе масса покоя равна полной массе при u = v. С учётом этого, подставляя в (13) значение m₀’ из (12), получаем:

m’ = 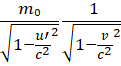.     (14)

Вследствие инвариантности полной массы частицы её величина в движущейся системе и в неподвижной одинаковы. В неподвижной системе полная масса даётся формулой (7). Приравнивая правые части формул (7) и (14), после простых преобразований получаем уравнение связи скоростей в неподвижной и движущейся системах отсчёта при u > v:

u² = v² + u’² - v² 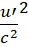 (15)

А из (15) получаем формулы непосредственно для u и u’:

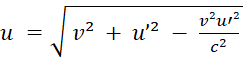,    (16)

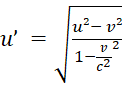.      (17)

Не трудно убедиться, что формулы (16) и (17) удовлетворяют требованию не превышения значениями u и u’ (в левой части формул) величины скорости света в вакууме c, если в правой части этой величины не превышает ни одна из переменных. А из (17) сразу видно, что формула применима только при соблюдении условия u≥v.

Наконец, рассмотрим наиболее сложный случай, когда u <v и скорость частицы в подвижной системе будет отрицательной (-u’). Начальная расчётная масса покоя, как и в предыдущем случае, может быть определена по (12), т.е. в предположении, что u = v. При этом полная масса частицы определяется также по формуле (12), как и в рассмотренных выше случаях. Реальная полная масса в неподвижной системе определяется и в этом случае по (7). Но использовать эту формулу для движущейся системы в данном случае мы не можем. Ведь, чтобы прийти в этой системе отсчёта к скорости частицы, соответствующей её реальному значению в неподвижной системе, эту скорость нужно уменьшать. В соответствии с формулой (10) это значит, что потребуется уменьшать полную массу частицы. А формула (7) получена для случая увеличения полной массы путём поглощения частицей массы движения извне (например, в ускорителях частиц из электрических и магнитных полей). Но уменьшение полной массы частицы означает излучение некоторой доли массы движения частицы, имеющей направление движения то же, что и сама частица. Но поскольку при u = v полная масса равна массе покоя, значит при этом уменьшается и масса покоя, а при выводе (7) масса покоя не изменялась. Причём уменьшение массы покоя будет вдвое больше уменьшения полной массы. Ведь из оставшейся полной массы частицы, доля массы, равная по величине доле излученной массы движения, но имеющей противоположное направление движения, является уже массой движения, задающей частице движение в отрицательном направлении. По-видимому, сейчас требуются пояснения, поскольку здесь может возникнуть вопрос о том, как одна частица может содержать в себе массы движения разных направлений.

На этот счёт использовалось следующее предположение. Когда масса движения переходит в массу покоя, характер движения носителя этой массы из прямолинейного меняется на замкнутое, например (самое простое), по окружности - движение ведь не может просто исчезнуть. Понятно, что при этом имеются элементы массы движения различных направлений, и для каждого из этих элементов можно найти двойника, имеющего ту же массу, но с противоположным направлением движения. Суммарное количество движения у каждой пары таких элементов равно нулю, и в результате частица остаётся в покое. При этом кинетическая энергия массы движения переходит во внутреннюю кинетическую энергию массы покоя. Будем называть её замкнутой для отличия от кинетической энергии массы движения, которую при необходимости избежать путаницы будем называть свободной. А при обратном превращении замкнутая кинетическая энергия переходит в свободную кинетическую энергию. Воздействие одних тел на другие осуществляется путём передачи массы движения, обладающей свободной энергией.

Итогом всего вышесказанного является необходимость вывода для рассматриваемого случая новой зависимости массы от скорости. Впрочем, решение этой проблемы оказалось проще, чем её осознание. Оно заключается в том, что при интегрировании дифференциального уравнения (6) нужно изменить пределы интегрирования – проинтегрировать левую часть от m₀֓ до m֓, а правую – от 0 до -u֓. В результате с учётом того, что m₀֓ определяется по (12), получено:

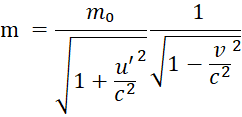.    (18)

Приравнивая правые части формул (7) и (18), после простых преобразований получаем уравнение связи скоростей в неподвижной и движущейся системах отсчёта при u < v:

u² = v² - u’² + v² 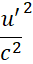.     (19)

А из (19) получаем формулы непосредственно для u и u’:

u =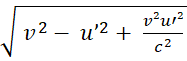,      (20)

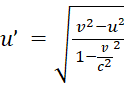.    (21)

Как и формулы (16) и (17) формулы (20) и (21) удовлетворяют требованию не превышения значениями u и u’ (в левой части формул) величины скорости света в вакууме c. А из (21) сразу видно, что формула применима только при соблюдении условия u≤v.

Таким образом, задачи специальной теории относительности решены без использования преобразований Лоренца с вытекающими из них следствиями, не имеющими экспериментальных подтверждений.

Выводы

1. Использование преобразований Лоренца как математической основы специальной теории относительности привело к возникновению эффектов, не имеющих экспериментальных подтверждений.
2. В создании мнения, что специальная теория относительности, напротив, имеет убедительные экспериментальные подтверждения, решающую роль сыграла почти полная идентичность формулы зависимости массы от скорости в теории относительности Эйнштейна и выведенной несколько позже формулы Льюиса. Но используемые в этих формулах значения скорости относятся к разным объектам. И экспериментальные подтверждения имеет только формула Льюиса.
3. Распространение принципа относительности на электромагнитные явления не требует изменения преобразований Галилея для координат при переходе от одной инерциальной системы отсчёта к другой. Изменение преобразований требуется только для скоростей. Вывод этих преобразований приведен в данной статье.