Введение. Наиболее важным на сегодняшний день направлением является автоматизация управления группами БЛА. Это становится возможным благодаря развитию средств вычислительной техники и математического аппарата. Сам по себе БЛА является лишь частью сложного многофункционального комплекса. В отличие от пилотируемой авиации для БЛА требуются дополнительные элементы системы обеспечения. Возможность учета предъявляемых к группе БЛА требований, таких как востребованность информации, и ее уникальность; пересечение маршрутов выдвижения летательных аппаратов и, при их пересечении они должны быть распределенными во времени.
Решение задачи. Для выбора решений рассматривается метод анализа, когда все возможные исходы известны и вероятности их наступления оцениваются с помощью функции принадлежности. Здесь используются результаты теории ожидаемой полезности, обобщенные на нечеткий случай.
Необходимо выбрать одно из двух решений, описываемых действиями A и B, которые зависят от различных случайных событий. В действии A имеется вероятность p на результат, полезность которого равна U1, и вероятность (1 – p) – получение результата с полезностью U2. Используя правила теории ожидаемой полезности, выбирают эту лотерею тогда и только тогда, когда pU1 + (1 – p) U2 > qV1 + (1 – q)V2. Здесь величины и, следовательно, степень предпочтения одной альтернативы другой точно неизвестны.
Пусть µА(а) и µB(b) – степени принадлежности а, b множествам ожидаемых полезностей лотерей A и B, тогда согласно принципу обобщения
|
µА(а) = max ( min (µp(p), µA1(U1), µA2(U2)); pU1 + (1 – p)U2 |
(1) |
|
µB(b) = max ( min (µQ(q), µB1(V1), µB2(V2)); qV1 + (1 – q)V2 |
(2) |
где µp (p) – степень принадлежности p множеству возможных значений для этой вероятности.
Наблюдается значительное перекрытие между двумя распределениями, и, хотя пик функции µА(x) имеет место при большем значении, чем пик функции µB(x), этого недостаточно для утверждения, что A лучше B.
Для оценки степени, с которой A предпочтительнее B, необходимо воспользоваться следующим методом:
|
µ(X → Y) = µ( ) =max((1- µ(X), µ(Y)). |
(3) |
Из выражения видно, что степень, с которой из некоторого нечеткого предложения X следует какое-то другое нечеткое предложение Y, есть степень истинности высказывания «Или не X, или Y». Последняя, в свою очередь равна большему из значений степени истинности «не X» степени истинности «Y». В более общей постановке, если X и Y есть нечеткие отношения между двумя переменными a и b, представляемые функциями принадлежности µx(a, b) и µy(a, b),
|
µ(X → Y) = min( max (µx(a, b), µy(a, b))). |
(4) |
Это определение смысла нечеткого высказывания не является единственно возможным, но оно достаточно эффективно для рассматриваемых целей.
Пусть Y – утверждение о предпочтении:
Y1: «A строго предпочтительнее B»,
|
µY1 (a, b) = |
(5) |
Y2: «A в некоторой степени предпочтительнее B»,
|
µY2 (a, b) = |
1, если a≥(b+k); 0,5+l(a-b), если (b+k)≤a≤(b-k); (6) 0, если a≤(b-k),) |
где µx (a, b) – степень, с которой a принадлежит множеству ожидаемых полезностей для действия A и b – множеству из действия B. Из этого следует, что
|
µx (a, b) = min (µA(a), µB(b)). |
(7) |
При таких определениях можно использовать (4) для вычисления степени предпочтения:
|
µ(X → Y1) = min( max (1 – µx(a, b), µy1(a, b))) = = min( max (1 – min (µA(a), µB(b)), µy1(a, b))) . |
(8) |
Для a > b µy1(a, b) = 1. Если существует пара (a, b), для которой аргумент min меньше единицы, то a < b. Таким образом,
|
µ(X → Y1) = min( 1 – min (µA(a), µB(b))) = = 1 – max( min (µA(a), µB(b))). |
(9) |
Максимум имеет место в граничной точке при a = b. Следовательно,
|
µ(X → Y1) = 1 – max( min (µA(a), µB(b)), |
(10) |
а из рис. 10 получаем значения min (µA(a), µB(b)). Его максимальное значение 0,96, а µ(X → Y1) = 0,04. Аналогичные вычисления дают µ(X → Y2) = 0,12.
Степень истинности высказывания «A строго предпочтительнее B» меньше, чем высказывания «A в некоторой степени предпочтительнее B». Соответствующие степени истинности суждений о предпочтении B относительно A равны нулю, как и предполагалось.
Вывод. Построена модель решения задачи выбора решений, а также синтеза закона оптимального управления системой летательных аппаратов, которая, в свою очередь, обеспечивает максимальную вероятность выполнения поставленной задачи и в то же время расходует минимальное количество ресурсов. Следовательно, поставленная задача решена.

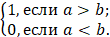
.png&w=640&q=75)