1. Введение
Композитные материалы обладают свойствами как пластичных материалов (металлы), так и хрупких (керамика, бетон) [1]. Конструкции, изготовленные из хрупких материалов, имеют особенность в потере прочности с увеличением их размеров. В механике материалов это называется масштабным эффектом. Влияние размерного эффекта широко изучалось для хрупких материалов, таких как бетон. После начала внедрения композитных материалов в крупные авиационные конструкции (фюзеляж, консоли крыла, хвостовое оперение), возник вопрос о влиянии такого эффекта на прочностные свойства.
Некоторые исследования в этой области были проведены в случаях растягивающей и изгибающей нагрузки [2-11]. Исследования влияния размерных характеристик композитных материалов при нагрузках на сжатие также проводились, но их значительно меньше [12-17]. Это можно объяснить сложностью в характере разрушения композитных материалов при сжатии. Результаты эксперимента, проведенного Gdoutos E. и Bazant Z. [12] на однонаправленном углепластике (UD) показал тенденцию к снижению прочности материала с увеличением его размера. Lee J. и Soutis C. [13] после проведения испытаний образцов, изготовленных из полимерного композита UD IM7/8552, заметили снижение прочности на 45% при увеличении линейных размеров в 4 раза. В исследовании Lee J. и Soutis C. [14] было определено, что в образцах из полимерного композитного материала, армированного волокнами T300/924C, микроизгиб волокон является критическим механизмом повреждения, который приводит к образованию полос перегиба и дальнейшему разрушению всей структуры. В этих работах было отмечено, что основным механизмом разрушения образцов было наличие микродефектов. По статистике, количество микродефектов увеличивается с увеличением размеров конструкции; это приводит к снижению прочности. На основе данных можно сделать вывод, что изучение микродефектов в композитах является важной частью понимания зависимости размерных характеристик от прочности при любых видах нагружения. Основным дефектом, вызывающим возникновение изломов и изгибов волокон, является отклонение волокон [18-24]. Изучение возникновения данного дефекта было выполнено учеными экспериментально [23, 25] и с использованием моделей с применением метода конечных элементов [26-30].
Остаются некоторые вопросы относительно зависимости прочности композита на сжатие от длины дефекта смещенного волокна при случаях со сжимающей нагрузкой, а также влияния таких дефектов на изменение прочности структуры композита на макроуровне.
Чтобы расширить знания в этой области, была разработана трехмерная модель репрезентативного элемента объема (RVE) композитного материала, армированного волокном в программном конечно-элементном комплексе Abaqus. Были изготовлены трехмерные микромеханические модели из углепластика с 4 и 20 волокнами с начальным дефектом отклоненного волокна. Моделирование поведения композитных образцов было произведено при сжимающем нагружении.
В результате были получены графики деформирования для каждого расчетного случая с образцами. Анализ показал о зависимости потере прочности от геометрических параметров образца с начальным отклонением волокна и от параметров самих дефектов. Было отмечено образование полосы перегиба при исследовании образцов с увеличенным количеством волокон, которая приводила к разрушению материала.
2. Методы и материалы
2.1. Геометрические и механические свойства
Модель идеализирует армированный волокнами композит в виде трехмерной микромеханической модели с двумя независимыми компонентами (волокно, матрица). Предполагается, что волокно линейно-упругий материал, механические характеристики которого приведены в таблице (табл. 1).
Поскольку дальнейший изгиб волокна должен вызывать необратимое разрушение матрицы, то она должна быть выполнена из материала, обладающего эластично-пластичными свойствами (табл. 1 и рис. 1).
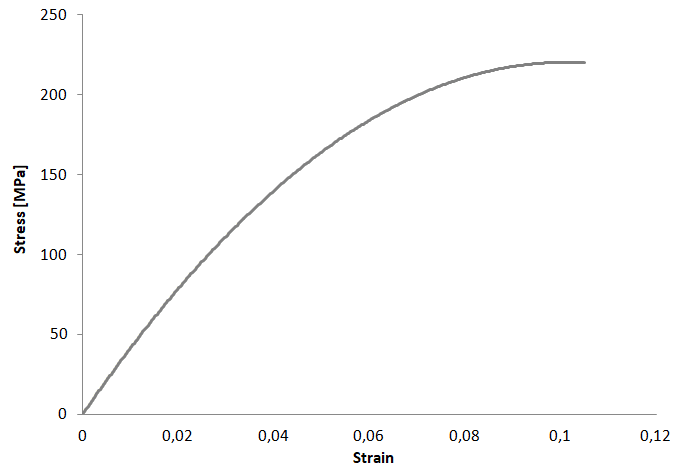
Рис. 1. Диаграмма деформирования матрицы композита
Таблица 1
Механические свойства волокна и матрицы
|
Ef1, GPa |
Ef2, GPa |
Ef3, GPa |
η12 |
η13 |
η23 |
Gf12, GPa |
Gf13, GPa |
Gf23, GPa |
Em, GPa |
η |
|---|---|---|---|---|---|---|---|---|---|---|
|
225 |
15 |
15 |
0.342 |
0.342 |
0.342 |
15 |
15 |
7 |
3.76 |
0.390 |
В первом случае использовались 8 трехмерных микромеханических моделей армированного волокнами композита с различными диаметрами волокон (df = 6, 8 мкм). Длина рабочей зоны с дефектом смещения волокна (рис. 2) имеет разные значения для каждого образца (Ld = 200, 300, 400, 500 мкм). Длина самого образца и отклонение, вызванное нагрузкой, варьируются пропорционально зоне дефекта. Площадь поперечного сечения всех образцов остается неизменной; ширина и высота показаны на рисунке (рис. 3а).
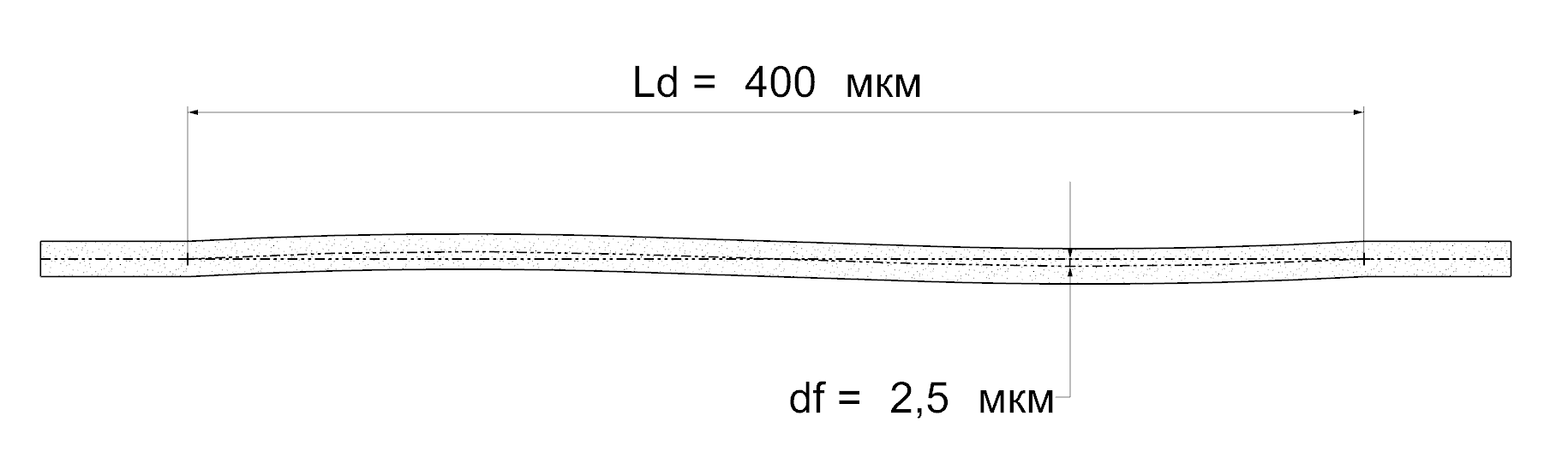Рис. 2. Геометрические параметры начального дефекта волокна
Во втором случае сравнивались 4 образца с диаметром волокна 6 мкм при объемной доле волокна 14% и 25%. Объемная доля волокна (vf) рассчитывается по формуле (1). Поперечные сечения данных образцов показаны на рисунке (рис. 3а) для vf = 14% и на рисунке (рис. 3б) для vf = 25% соответственно. Рабочие длины зон с дефектом составляют 200 и 300 мкм.
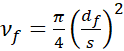(1)
В третьем случае используются трехмерные микромеханические модели композита с 20 волокнами. Рабочая длина образцов с несоосными волокнами составляет 500, 700, 800 мкм, а диаметры волокон – 6 и 8 мкм. Геометрические параметры поперечного сечения образцов с 20 волокнами показаны на рисунках (рис. 3в и рис. 3г).
Во всех случаях делается предположение, что начальный локальный дефект (отклонение волокна) используется для инициирования начала формирования изгиба волокна с последующим образованием полосы перегиба (kink-band). Как описано в исследованиях ученых [12-15], этот дефект непосредственно влияет на разрушение композита при сжатии и может повлиять на появление размерного эффекта на микроуровне. Дефект начального отклонения волокна представляет вид двумерной синусоиды с амплитудой 2,5 мкм в плоскости X-Y. Этот выбор обеспечивает более плавный переход от зафиксированных краев к рабочей зоне с дефектами.
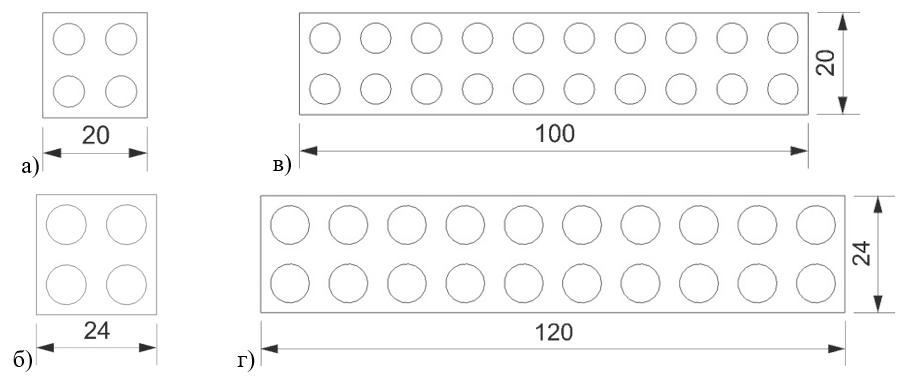Рис. 3. Геометрические параметры поперечных сечений образцов (все размеры в мкм)
2.2. Метод конечных элементов
Коммерческое программное обеспечение для инженерных расчетов Abaqus 2018 (Dassault Systems, Франция) используется для моделирования процесса сжатия образцов композита, армированного волокнами, с начальным дефектом отклоненного волокна. Конечно-элементная модель с 4 и 20 волокнами показана на рисунках (рис. 4а и рис. 4б). Для анализа используется сетка размером 5 мкм. Тип элемента сетки выбран C3D8R: An 8-node linear brick, reduced integration, hourglass control. Для модели применяются следующие граничные условия (рис. 5):
- Нижняя плоскость Y-Z: Зафиксирована вдоль осей X и Y.
- Передняя и нижняя плоскости X-Y: Зафиксированы вдоль оси Z.
- Передняя и нижняя плоскости X-Z (кроме рабочей зоны с дефектом): Зафиксированы вдоль оси Y.
Расчет был выполнен с использованием решателя ABAQUS/Static общего вида с включенным режимом нелинейной геометрии (nlgeom: on) для учета больших пластических деформаций матрицы.
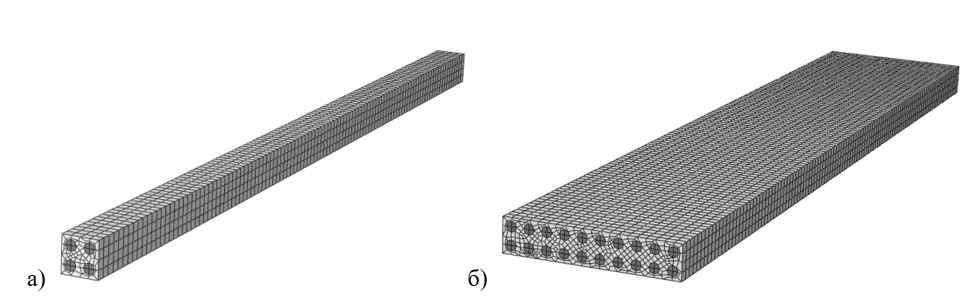
Рис. 4. Конечно-элементные модели образцов с 4 и 20 волокнами
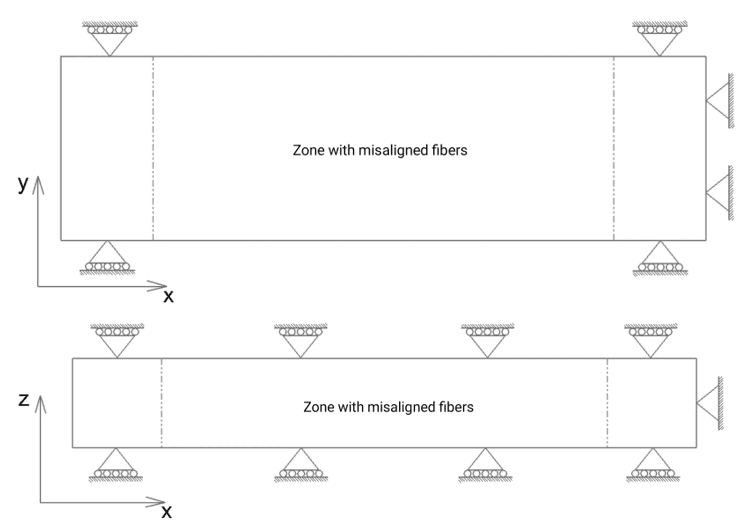
Рис. 5. Схематичное описание граничных условий, примененных в процессе моделирования
2.3. Схема нагружения
Трехмерная модель композита, представленная в предыдущих частях, подвергается воздействию осевой сжимающей нагрузки вдоль направления волокон. Необходимые свойства для анализа включают осевой модуль упругости волокна Ef1, поперечные модули упругости волокна: Ef2, Ef3, модули сдвига волокна: G12, G13, G23, модуль упругости матрицы Em, предел текучести матрицы σs (см. табл. 1) и степень первоначального смещения волокна.
Результатами анализа для всех случаев были графики зависимости продольного напряжения σ11 от деформации ε, максимальная прочность на продольное сжатие SL(-) для всех образцов. Для получения данных параметров использовалась контрольная точка (Reference Point), которая в ходе анализа собирала значения реакция опоры RF1 и смещение U1 вдоль оси приложения сжимающей нагрузки для всего образца.
3. Результаты и их обсуждение
3.1. Случай 1. Влияние длины и диаметра поврежденных волокон на прочность образцов
На графиках (рис. 6а и 6б) показаны кривые деформирования для первого случая. На графиках можно выделить 2 области: первая область линейной деформации, которая описывается законом Гука, и область пластической деформации, за которой идет разрушение материала с потерей прочности образцов.
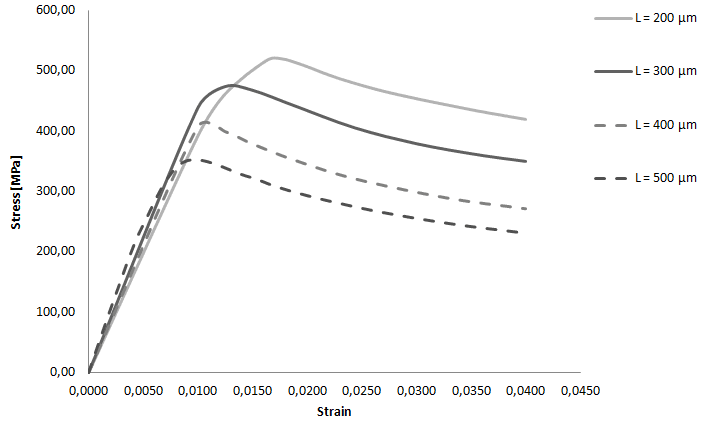
Рис. 6(а). График деформирования образцов с диаметром волокна 8 мкм
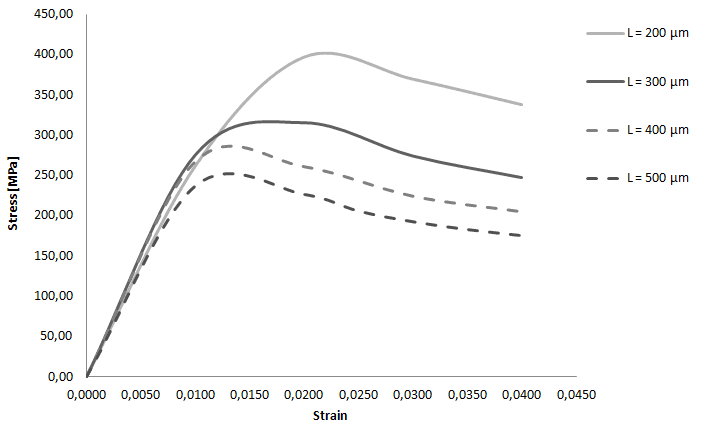
Рис. 6(б). График деформирования образцов с диаметром волокна 6 мкм
Графики показывают тенденцию к уменьшению значения критического напряжения σкр и значения критической деформации εкр с увеличением длины дефекта образца в среднем на 10%, как показано в таблице (табл. 2). На основе полученных данных можно сделать вывод, что при увеличении рабочей длины образца с дефектом отклоненного волокна, его прочность и жесткость снижается. Кроме того, значительные концентрации напряжений расположены с обеих сторон разорванного волокна (рис. 7). Хотя материал в целом находится в состоянии сжатия, волокна с обеих сторон подвергаются растягивающему напряжению, что было отмечено в экспериментах Pimenta S. [24].
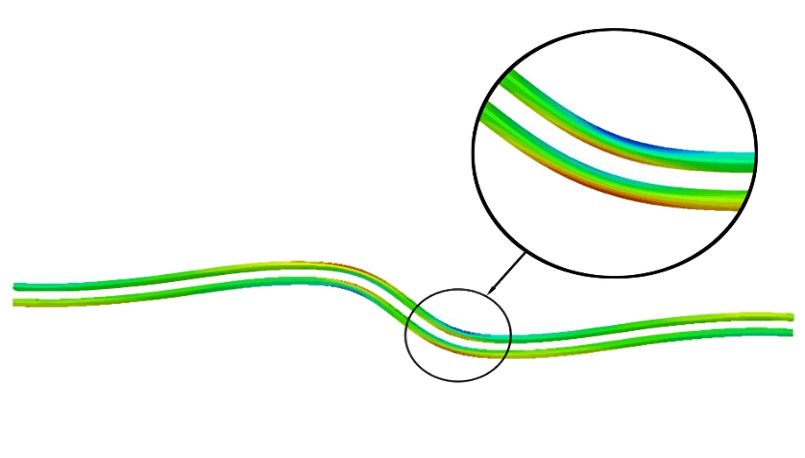
Рис. 7. Распределение продольных напряжений при изгибе волокна
Таблица 2
Максимальное напряжение в образцах с диаметром волокна 6 и 8 мкм и с различными длинами дефекта
|
Диаметр волокна [мкм] |
8 |
6 | ||||||
|
Длина зоны с дефектом [мкм] |
200 |
300 |
400 |
500 |
200 |
300 |
500 |
400 |
|
σкр [МPa] |
520.2 |
473.0 |
407.0 |
348.7 |
397.2 |
316.1 |
267.2 |
236.2 |
3.2. Случай 2. Влияние изменения объемной доли поврежденных волокон
В предыдущих экспериментах площадь поперечного сечения всех образцов была одинаковой. Следовательно, если диаметр волокна уменьшается, объемная доля волокна vf уменьшается. Для объективной оценки было изучено влияние длины дефектной зоны образца на прочность образца при нагрузке на сжатие, если диаметр волокна будет неизменным и равен 6 мкм, а объемная доля волокна будет 14 и 25 % (рис. 3а и рис. 3б) соответственно.
Прочность композита на сжатие в основном зависит от механических свойств деталей (волокна, матрицы) и от объемной доли волокон в композите. Когда объемная доля волокна уменьшается, увеличивается доля матрицы в материале, которая слабее, чем волокна. Однако матрица все еще может способствовать прочности композита на сжатие, обеспечивая опору и передавая напряжения между волокнами. Более того, при уменьшении объемной доли волокна, расстояние между волокнами увеличивается. Это может привести к лучшему распределению нагрузки внутри композита, снижая вероятность локального разрушения и повышая общую прочность на сжатие.
В данном случае (рис. 8) можно наблюдать ухудшение прочностных характеристик образцов при увеличении объемной концентрации матрицы, что согласуется с теорией.
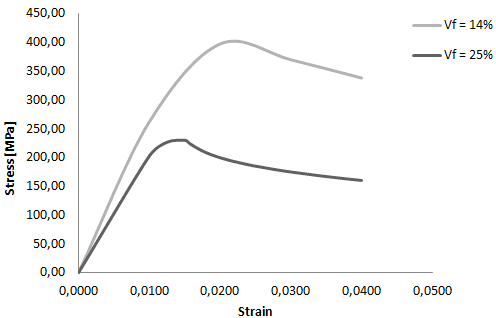
Рис. 8(а). График деформирования образцов с длиной дефекта 200 мкм
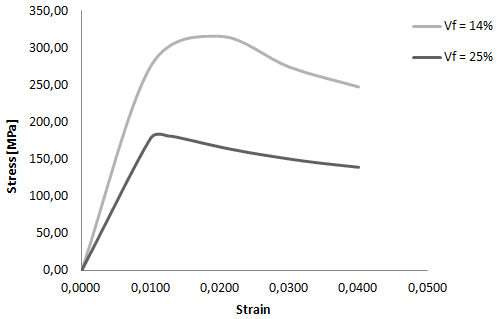
Рис. 8(б). График деформирования образцов с длиной дефекта 300 мкм
3.3. Случай 3. Результаты моделирования образцов с 20-ю волокнами
Общий подход в данной части заключался в сжатии большого количества волокон со свободными продольными краями, как это было выполнено Pimenta S. [24] и Ai-jun Li [31]. С помощью этого решения можно рассмотреть поведение большего количества волокон внутри образца, уменьшая эффект свободных краев для таких образцов.
На рисунке (рис. 9) показана зависимость напряжения от деформации для 2 образцов с одинаковой длиной зоны дефекта равной 500 мкм и объемной долей волокна равной 25%. На графике показано, что прочность образца с диаметром волокна 8 мкм больше, чем у образца с диаметром волокна 6 мкм. Эти результаты подтверждают результаты из части 3.1.
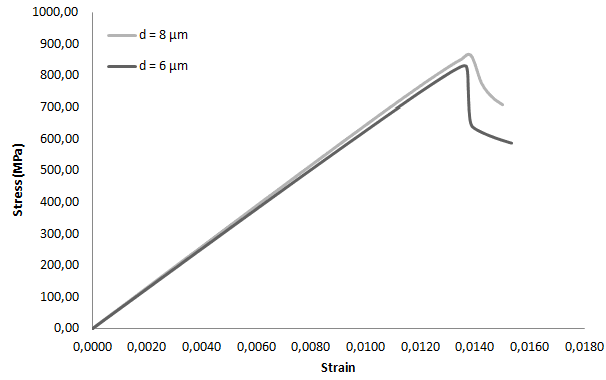
Рис. 9. График деформирования образцов с длиной дефекта 500 мкм
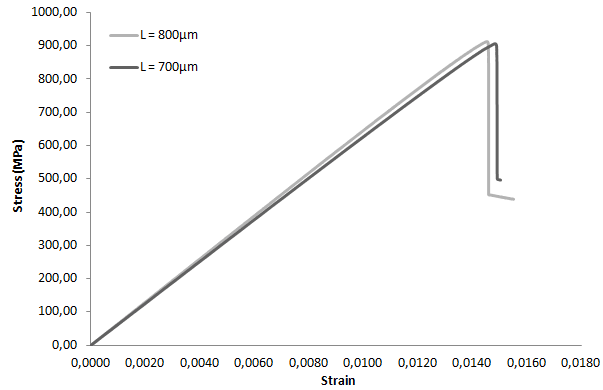
Рис. 10. График деформирования образцов с диаметром волокна 6 мкм
Далее, были рассмотрены 2 образца с одинаковым диаметром волокна равным 6 мкм и объемной долей волокна равной 25%. Длины зон с дефектами в первом и втором образцах составляли 700 и 800 мкм соответственно. Из результатов, показанных на графике (рис. 10), следует, что критическое напряжение, которое может вызвать деформацию волокна, выше в образце с длиной дефектной зоны 800 мкм, но при этом его жесткость ниже, образца с длиной зоны с дефектом равной 700 мкм. Эти значения отличаются от результатов экспериментов в части 3.1, где образцы с минимальной длиной зоны дефекта имели максимальную прочность. Можно предположить, что в образцах, содержащих больше волокон, наличие напряжения сдвига (σ12) и пластическая деформация матрицы с ее дальнейшим разрушением оказывают большое влияние на формирование несоосности волокон.
На рисунке (рис. 12) показано распределение напряжения сдвига σ12 на различных этапах сжатия образца с диаметром волокна df = 6 мкм и длиной зоны дефекта Ld = 700 мкм. Этапы соответствуют точкам 1-4 на кривой графика (рис. 11). Из-за наличия первоначального смещения волокон в зоне дефекта возникает концентрация напряжения сдвига. Зона концентрации напряжений непрерывно расширяется с увеличением нагрузки и в конечном итоге распределяется по всей ширине образца, что постепенно приводит к разрушению матрицы. Процесс образование полосы перегиба можно увидеть на рисунке (рис. 12), где каждый этап соответствует точкам 1-4 на графике (рис. 11). Пластическая деформация матрицы начинается в начальной зоне дефекта волокна и непрерывно увеличивается под действием сжимающей нагрузки. Во время пластической деформации матрицы волокно теряет свою опору, и начинает происходить изгиб волокон. Когда полоса текучести матрицы проходит по всей ширине образца, возникает полоса перегиба с дальнейшем разрушением образца.
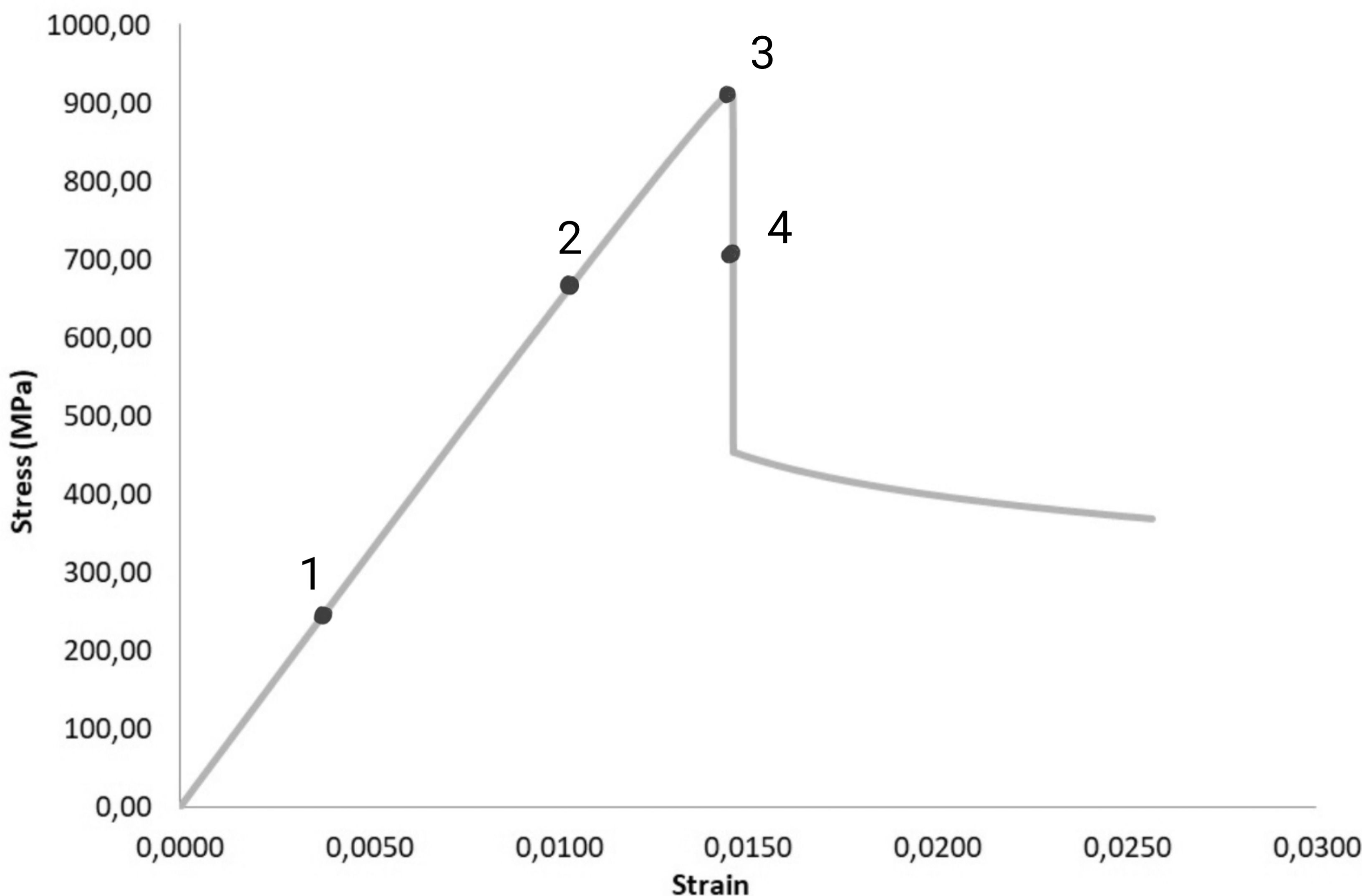
Рис. 11. График деформирования с этапами возникновения полосы перегиба
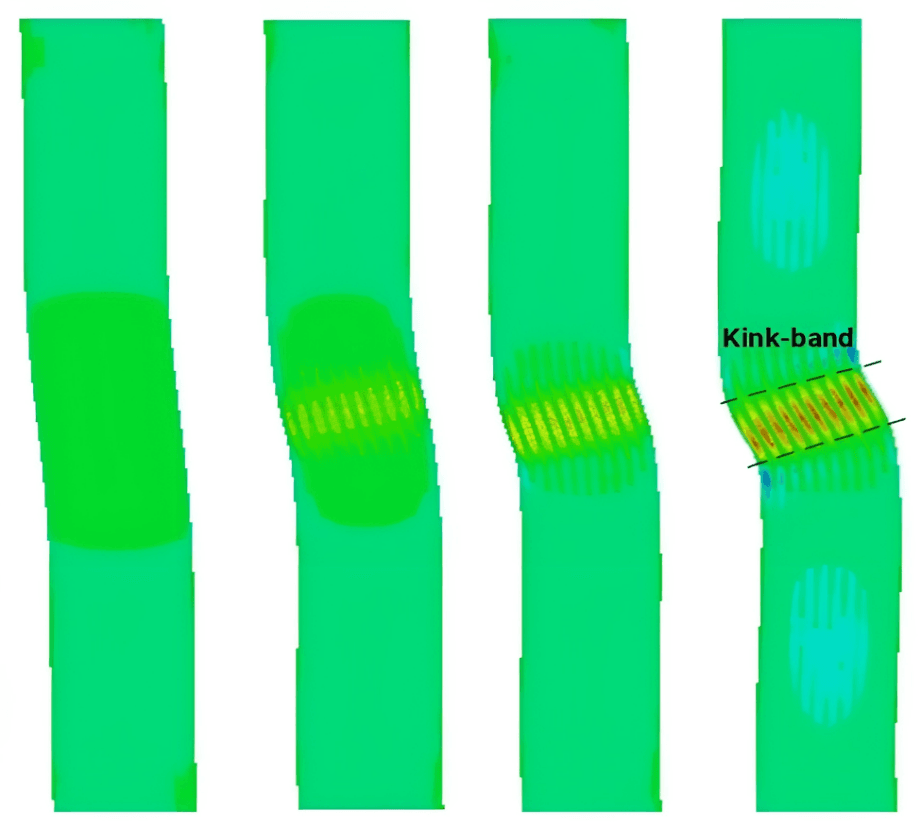
Рис. 12. Изображение образца с этапами возникновения полосы перегиба
4. Вывод
Исследуя влияние размера дефекта на прочность композитного материала, было проведено моделирование трехмерных образцов репрезентативного элемента объема ПКМ. Анализ прочности проводился в коммерческого программного обеспечения для инженерного расчета Abaqus 2018, в этой программе была изготовлена трехмерная модель репрезентативного элемента объема композитного материала, состоящего из эластичного волокна и упругопластичной матрицы. Чтобы инициировать разрушение, каждый образец имел начальный дефект в виде отклоненных волокон. Результаты показали, что основная причина разрушения образцов при таком случае стало образование полос перегиба волокон (kink-band).
Результаты показали, что наличие дефекта отклоненного волокна может повлиять на прочность композита на сжатие. Следовательно, можно предположить, что размерный эффект, который зависит от внутренних микромеханических дефектов, присутствует в композитной конструкции и должен учитываться при проектировании крупномасштабных конструкций.
